Learning to Time-Decode in Spiking Neural Networks Through the Information Bottleneck
郑重声明:原文参见标题,如有侵权,请联系作者,将会撤销发布!

Abstract
训练脉冲神经网络(SNN)的一个关键挑战是,目标输出通常以自然信号的形式出现,例如用于分类的标签或用于生成模型的图像,并且需要编码为脉冲。这是通过手工制作目标脉冲信号来实现的,这又隐式地固定了用于将脉冲解码为自然信号的机制,例如发放率解码。目标信号和解码规则的任意选择通常会削弱SNN在脉冲时刻编码和处理信息的能力。为了解决这个问题,本文介绍了一种混合变分自动编码器结构,包括编码SNN和解码人工神经网络(ANN)。解码ANN的作用是学习如何将SNN输出的脉冲信号最佳地转换为目标自然信号。引入了一种新的端到端学习规则,通过替代梯度优化有向信息瓶颈训练准则。我们演示了该技术在各种任务(包括真实数据集)的实验环境中的适用性。
1 Introduction
虽然传统的人工神经网络(ANN)实现了基于静态发放率的神经元,但脉冲神经网络(SNN)结合了更接近其生物对应物的基于动态脉冲的神经元模型。在不同的社区中,SNN要么被用作生物大脑运作的模型,要么被用作认知任务的有效解决方案。当在专用硬件上实现SNN时,SNN的效率取决于脉冲时间信息编码的高容量、低延迟和高噪声容忍度[1]。利用新型原型芯片的最新结果证实了几个优化和推理问题在延迟和能量精度度量方面的潜在数量级增益[2]。相比之下,SNN的训练算法的前景仍然相当混乱[2],一个关键的开放问题是如何导出能够最佳利用脉冲神经元的时间编码能力的学习规则。这是这项工作的重点。
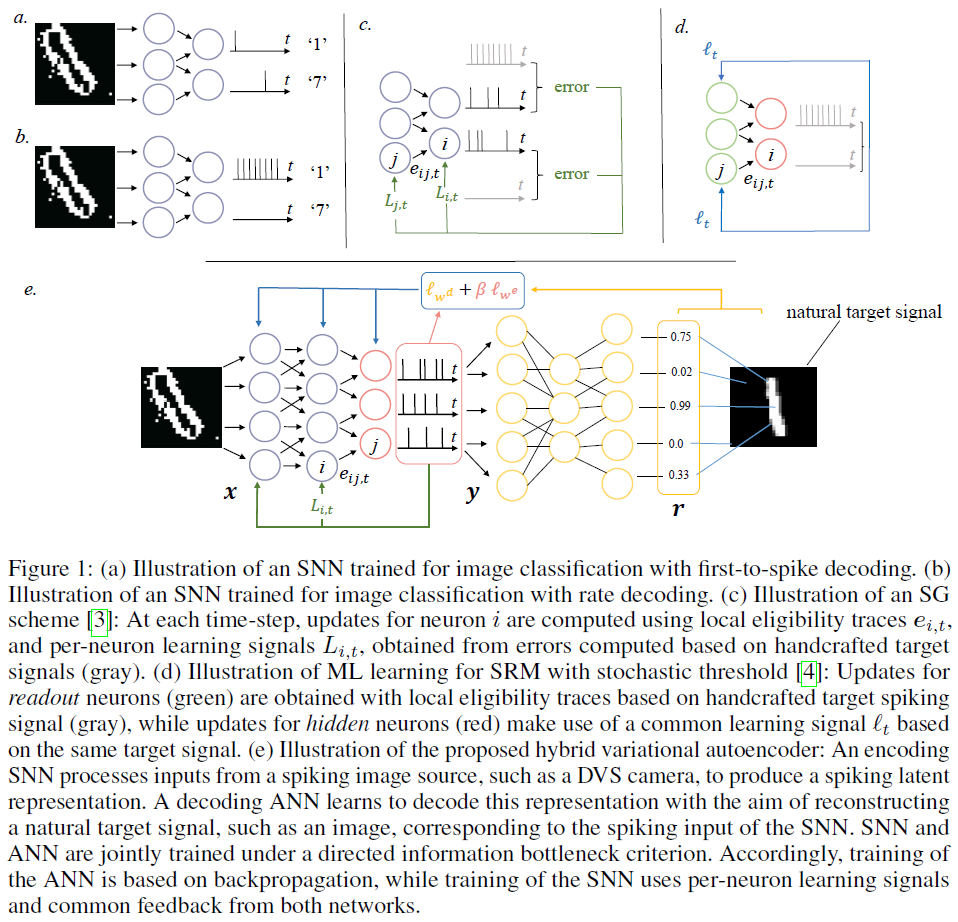
Learning how to decode. 考虑一下训练SNN的问题——一个由脉冲神经元组成的网络。为了修正这些想法,如图1(a)-(b)所示,假设我们希望训练SNN来对来自神经形态传感器的输入进行分类,例如DVS摄像机[5],这些输入以脉冲信号集合的形式。因此,我们有一个脉冲信号作为输入,一个自然信号(标签)作为输出。作为图1(e)中的另一示例,我们可能希望“自然化”DVS相机的输出,以产生相应的自然图像[6]。SNN的直接训练取决于SNN输出上的损失函数的定义。这通常通过将目标自然信号转换为用作SNN期望输出的脉冲信号来完成。如图1(a)-(b)所示,例如,可以向代表正确类别的读出神经元分配大发放率脉冲信号或更早的脉冲。然后,损失函数测量实际输出脉冲信号和相应脉冲目标之间的差异。
前一段中概述的方法有一个重要问题:通过选择手工制作的目标脉冲信号,可以有效地事先选择SNN允许产生的脉冲信息编码类型。这限制了SNN充分利用脉冲信号的时间编码能力。例如,图1(a)中概述的目标信号对应于假设初次脉冲(first-to-spike)解码,而图1(b)中的目标信号则对应于发放率解码[7]。本文提出了一种方法,该方法允许SNN自动学习如何将输入最佳编码为脉冲信号,而无需先验地约束解码策略。
为此,我们介绍了图1(e)所示的混合SNN-ANN自动编码器架构,该架构由编码SNN和解码ANN组成。解码ANN的作用是学习如何将SNN输出的脉冲信号最佳地转换为目标自然信号。对编码SNN和解码ANN进行端到端训练,以确保SNN产生基于信息脉冲的表示。
Directed information bottleneck. 如何联合训练混合SNN-ANN自动编码器?一方面,我们希望SNN的脉冲输出能够提供有关目标自然信号的信息(我们将其称为参考信号),另一方面,希望SNN脉冲输出能够去除脉冲输入中不提供有关参考信号信息的所有外来信息。为了满足这一双重需求,我们采用了信息瓶颈(IB)公式[8],并将ANN视为变分自动编码器系统中的推理网络[9]。
在将变分IB方法应用于图1(e)中的混合SNN-ANN自动编码器中,我们做出了两个关键贡献。1) 给定SNN的固有动态操作,我们将IB标准推广到有向信息度量[10],以代替传统的互信息。我们将所得方法称为变分有向IB(VDIB)。2) 为了实现信息论度量(如IB)的优化,我们引入了一个SNN模型,该模型包含确定性隐藏神经元和概率读出神经元。在这样做的过程中,我们结合了训练SNN的两个方面的研究:第一条线纯粹专注于确定性模型,将SNN视为递归神经网络(RNN),并通过替代梯度(SG)技术导出时间反向传播(BPTT)的近似值[3, 11-15];而第二种方法仅假设概率神经元,导出最大似然(ML)学习的近似值。有关相关工作的更多讨论可在下一节中找到。
2 Related works
Training SNNs. 近年来,用于训练SNN的SG技术获得了巨大的发展势头,成为最先进的技术,事实上超过了其他技术。如[12]中所述,这些技术依赖于替代衍生物来替代脉冲神经元阶跃激活功能的不明确衍生物。SG与BPTT的截断和近似版本相结合,包括使用每层局部误差信号[13]和使用直接反馈对准定义的每神经元学习信号[3, 15]。概率SNN的学习规则通常是通过处理ML问题得出的,并导致依赖于随机采样和普通(而不是每个神经元)学习信号的更新。该方法被证明可以推广到赢者通吃的神经元网络[16]。如图1所示,所提出的方法建立在两个模型上,以便能够使用SG方法优化概率学习标准。
Hybrid SNN-ANN architectures. [17]中最近提出了一种基于变分自动编码器(VAE)框架的混合SNN-ANN架构,用于手势相似性分析。尽管产生了类似的目标,[17]中的编码器没有完全脉冲,因为ANN接收SNN读出层中脉冲神经元的膜电位。我们工作中提出的模型避开了这一限制。
Information bottleneck. IB技术起源于二十年前[8],在假设离散变量的率失真问题形成的背景下。近年来,该方法重新引起了人们的兴趣,首先是作为解释ANN性能的手段[18],然后是[9]中的训练标准。我们通过考虑因果关系约束下的时间信号来扩展IB,从而用有向信息代替相互信息[10]。IB原理先前已在SNN文献中用于单个神经元的情况[19, 20]。最后,它已在理论神经科学中用于解释感觉神经元的处理[21],并作为预测和有效编码理论的统一原则。我们的模型包含[21]中介绍的框架。
3 Problem definition
Notations. 考虑三个联合分布的随机向量x, y, z具有分布p(x, y, z)。给定z的x和y之间的条件互信息(MI)定义为![]() ,其中Ep[·]表示关于分布p的期望。在同一概率空间上定义的两个概率分布p(x)和q(x)之间的Kullback-Leibler (KL)散度为
,其中Ep[·]表示关于分布p的期望。在同一概率空间上定义的两个概率分布p(x)和q(x)之间的Kullback-Leibler (KL)散度为![]() 。
。
对于从时间1到T的任意两个联合分布的随机向量a=(a1, ... , aT)和b=(b1, ... , bT),给定b下a的τ-因果条件分布定义为:
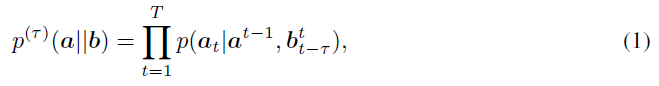 其中,我们表示
其中,我们表示![]() 为从时间t1+1到t2的总随机向量,并写入
为从时间t1+1到t2的总随机向量,并写入![]() ;该分布(1)捕获序列a对b的最后τ样本的因果依赖性。如果τ=T,我们恢复因果条件分布[10]。
;该分布(1)捕获序列a对b的最后τ样本的因果依赖性。如果τ=T,我们恢复因果条件分布[10]。
我们还将τ≥0的τ-有向信息定义为:
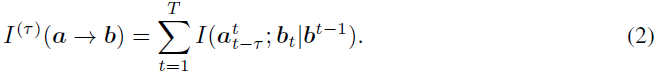
该度量量化了从序列a到b的最后τ样本的因果统计相关性。当τ=T时,这将恢复标准定向信息[10]。我们表示为卷积算子![]() 。
。
Problem definition. 我们研究了图1中的混合SNN-ANN自动编码器架构,目的是训练SNN编码器以产生脉冲输入x的时间编码脉冲表示y,该脉冲表示y是关于自然参考信号r的信息。在整个过程中,脉冲信号是二值矢量序列,其中“1”表示脉冲,而自然信号是实值矢量序列。在图1(e)中的原型应用中,输入x从神经形态传感器(如DVS摄像机[5])获得,参考信号r表示相应的目标自然信号,如标签或原始自然图像。SNN产生的脉冲表示y被馈送到ANN,其作用是将y解码为参考信号r。重要的是,我们没有先验地约束解码策略。相比之下,现有的工作通常手工制作对应于某些固定解码规则的目标脉冲信号y,例如发放率解码(图1(a)-(b))。我们的主要贡献是一种联合训练编码SNN和解码ANN的方法,目的是从编码SNN产生的脉冲信号中发现自动有效的时间解码规则。
(略)
4 Learning to decode through the IB
5 SNN Model
Deterministic SRM.
SRM with stochastic threshold.
Gradients.
6 Experiments
我们现在在实验环境中评估所提出的VDIB解决方案。我们特别关注两项任务:预测编码和脉冲信号的自然化。前一项任务突出了因果、在线、编码和解码的方面,并与理论神经科学的工作密切相关[21]。相比之下,后一项任务强调了所提出的神经形态计算方法的作用[6]。具体而言,脉冲输入的自然化,例如,从DVS摄像机[5]获得的脉冲输入,能够将神经形态传感器与传统数字传感器和处理器集成[6]。由于所提出的混合架构在选择解码ANN时具有灵活性,我们考虑了三种选择:(i)简单的逻辑回归模型,(ii)具有一个隐藏层的多层感知机(MLP),以及(iii)具有两个卷积层和一个全连接层的卷积神经网络(CNN)。如第3节所述,在每个时间 t,解码ANN被赋予序列![]() 由编码SNN产生的时间样本中的τd个。作为基准,我们还考虑了传统的发放率解码,即序列
由编码SNN产生的时间样本中的τd个。作为基准,我们还考虑了传统的发放率解码,即序列![]() 内的时间采样随时间求和,得出
内的时间采样随时间求和,得出![]() 在被馈送到ANN之前。通过考虑使用分层架构对网络进行编码,我们对ANN和SNN的实现利用了自动差分、通用深度学习库[27]和Tesla V100 GPU。
在被馈送到ANN之前。通过考虑使用分层架构对网络进行编码,我们对ANN和SNN的实现利用了自动差分、通用深度学习库[27]和Tesla V100 GPU。
6.1 Efficient predictive coding
6.2 Naturalizing MNIST images
6.3 Naturalizing MNIST-DVS images
7 Conclusion




 浙公网安备 33010602011771号
浙公网安备 33010602011771号