Fully Spiking Variational Autoencoder
郑重声明:原文参见标题,如有侵权,请联系作者,将会撤销发布!

AAAI 2022
Abstract
脉冲神经网络(SNN)由于其二值和事件驱动的性质,可以在具有超高速和超低能耗的神经形态设备上运行。因此,SNN有望有各种应用,包括作为在边缘设备上运行的生成模型来创建高质量图像。在这项研究中,我们构建了一个带有SNN的变分自动编码器(VAE),以实现图像生成。VAE以其在生成模型中的稳定性而闻名;最近,它的质量提高了。在原始VAE中,潜在空间表示为正态分布,采样时需要进行浮点计算。然而,这在SNN中是不可能的,因为所有特征都必须是二值时间序列数据。因此,我们用自回归SNN模型构建了潜在空间,并从其输出中随机选择样本来对潜在变量进行采样。这允许潜在变量遵循伯努利过程,并允许变分学习。因此,我们构建了全脉冲变分自动编码器,其中所有模块都使用SNN构建。据我们所知,我们是第一个仅使用SNN层构建VAE的工作。我们用几个数据集进行了实验,并证实与传统ANN相比,它可以生成质量相同或更好的图像。该代码位于https://github.com/kamata1729/FullySpikingVAE.
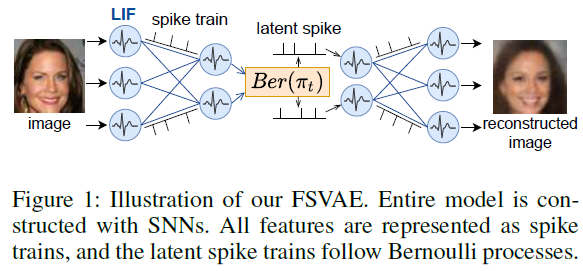
Introduction
最近,人工神经网络(ANN)发展迅速,并在计算机视觉和NLP中取得了相当大的成功。然而,ANN通常需要大量的计算资源,这在计算资源有限的情况下是一个挑战,例如在边缘设备上。
脉冲神经网络(SNN)是比ANN更准确地模拟生物大脑结构的神经网络;值得注意的是,SNN被称为第三代人工智能(Maas 1997)。在SNN中,所有信息都表示为二值时间序列数据,并由基于事件的处理驱动。因此,SNN可以在神经形态设备上以超高速和超低能耗运行,如Loihi(Davies等人,2018)、TrueNorth(Akopyan等人,2015)和Neurogrid(Benjamin等人,2014)。例如,在TrueNorth上,计算时间大约比传统ANN低1/1000,能耗大约比传统的ANN低1/10万倍(Cassidy等人,2014)。
随着最近对神经网络的突破,SNN的研究进展迅速。此外,SNN在MNIST、CIFAR10和ImageNet分类任务中的准确性优于ANN(Zheng等人,2021;Zhang和Li 2020)。此外,SNN用于目标检测(Kim等人,2020)、声音分类(Wu等人,2018)、光流估计(Lee等人,2020年);然而,它们的应用仍然有限。
特别是,尚未充分研究基于SNN的图像生成模型。Spiking GAN(Kotariya和Ganguly,2021)利用浅层SNN构建了一个生成器和鉴别器,并通过对抗性学习生成手写数字图像。然而,它的生成质量很低,并且生成了一些不希望的图像,这些图像不能被解释为数字。在(Skatchkovsky、Simeone和Jang,2021)中,SNN用作编码器,ANN用作解码器,以构建VAE(Kingma和Welling,2014);然而,他们研究的主要焦点是有效的脉冲编码,而不是图像生成任务。
在ANN中,图像生成模型已被广泛研究,可以生成高质量图像(Razavi、van den Oord和Vinyals 2019;Karras等人,2020)。然而,一般来说,图像生成模型在计算上是昂贵的,对于边缘设备或实时生成,必须解决一些问题。如果SNN可以生成与ANN类似的图像,那么它们的高速和低能耗可以解决这些问题。
因此,我们提出了全脉冲变分自编码器(FSVAE),它可以生成与ANN相同或更好质量的图像。VAE以其在生成模型中的稳定性而闻名,并与生物大脑的学习机制有关(Han等人,2018)。因此,构建VAE与SNN是兼容的。在我们的FSVAE中,我们在SNN中构建了整个模型,以便将来可以在神经形态设备中实现。我们使用MNIST(Deng 2012)、FashionMNIST(Xiao、Rasul和Vollgraf 2017)、CIFAR10(Krizhevsky和Hinton 2009)和CelebA(Liu等人2015)进行了实验,并证实FSVAE可以生成与相同结构的ANN VAE相同或更好质量的图像。未来,FSVAE可以在神经形态设备上实现,预计在速度和能耗方面会有所改善。
在SNN中创建VAE最困难的方面是如何创建潜在空间。在ANN VAE中,潜在空间通常表示为正态分布。然而,在SNN的框架内,从正态分布采样是不可能的,因为所有特征都必须是二值时间序列数据。因此,我们提出了自回归伯努利脉冲采样。首先,我们将VRNN的思想(Chung等人,2015)纳入SNN,并使用自回归SNN构建了先验和后验模型。潜在变量是从自回归SNN的输出中随机选择的,这使得能够从伯努利过程中进行采样。这可以在神经形态设备上实现,因为它不需要像ANN中那样在采样期间进行浮点计算,并且可以在实际的神经形态设备中使用随机数生成器进行采样(Wen等人,2016;Davies等人,2018)。此外,潜在变量可以顺序采样;因此,它们可以增量地输入到解码器,这节省了时间。
本研究的主要贡献总结如下:
- 我们提出了自回归伯努利脉冲采样,它使用自回归SNN并将潜在空间构造为伯努利过程。这种采样方法在SNN框架内是可行的。
- 我们提出了全脉冲变分自编码器(FSVAE),其中所有模块都在SNN中构建。
- 我们对多个数据集进行了实验;FSVAE可以生成与相同架构的ANN VAE相同或更好质量的图像。
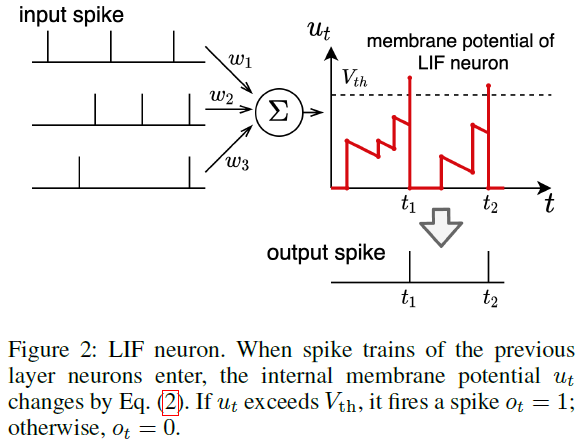
Related Work
Development of SNNs
Spike Neuron Model
Variational Autoencoder
Variational Recurent Neural Network
Generative models in SNN
脉冲GAN(Kotariya和Ganguly 2021)使用两层SNN构造生成器和鉴别器来训练GAN;生成的图像的质量低。其中一个原因是,初次脉冲时间编码(time-to-first spike encoding)不能在脉冲序列的中间抓取整个图像。此外,由于SNN的学习是不稳定的,因此在没有正则化的情况下很难执行对抗性学习。
Applying VAE on SNN
一些研究部分使用SNN来创建VAE。在(Stewart等人,2021)中,用DVS摄像机拍摄的人体手势视频被输入到SNN编码器,潜在变量由输出神经元的膜电位生成;ANN解码器从中重建输入。他们的研究旨在为新手势生成伪标签,而不是生成图像。此外,由于解码器是用神经网络构建的,因此整个模型无法在神经形态设备上实现。类似地,(Skatchkovsky,Simeone和Jang 2021)也有同样的问题,因为他们的解码器也是用ANN构建的。
在SVAE(Talafha等人,2020)中,在训练基于ANN的VAE后,他们将其转换为SNN,以使用STDP执行无监督学习,然后再次将其转换成ANN,以提高生成图像的质量。因此,没有研究SNN的图像生成。
一些研究使用概率神经元来执行变分学习(Rezende、Wierstra和Gerstner,2011;Bagheri 2019)。然而,由于概率神经元使用泊松过程的采样,因此需要额外的采样模块。因此,我们在更常用的确定性SNN中创建了一个完整的图像生成模型。
Autoregressive Model for Spike Train Modeling
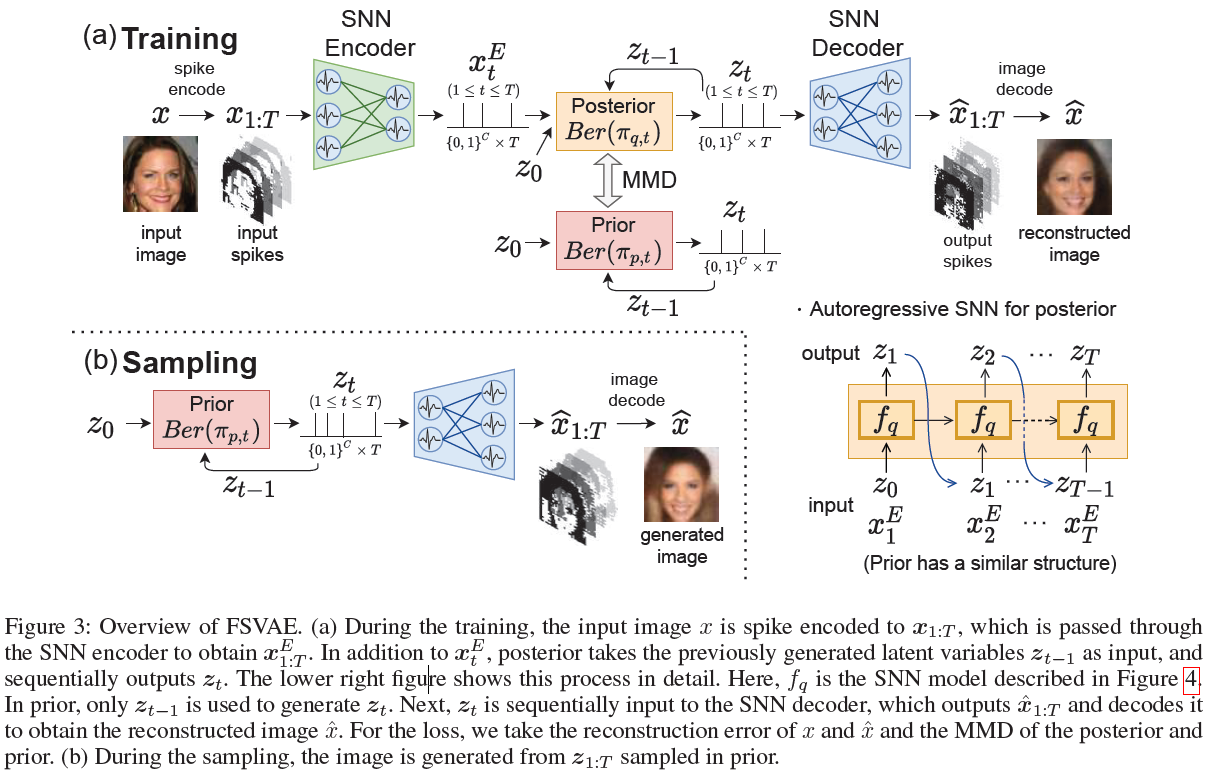
Proposed Method
Overview of FSVAE
详细的网络架构可在补充材料A中找到。
图3显示了模型概述。使用直接输入编码(Rueckauer等人,2017)将输入图像 x 转换为脉冲序列x1:T,并随后输入到SNN编码器。从编码器的输出脉冲序列![]() ,后验器递增地输出潜在脉冲序列z1:T。然后,SNN解码器生成输出脉冲序列
,后验器递增地输出潜在脉冲序列z1:T。然后,SNN解码器生成输出脉冲序列![]() ,其被解码以获得重建图像
,其被解码以获得重建图像![]() 。采样时,先验递增生成z1:T,并将其输入SNN解码器以生成图像
。采样时,先验递增生成z1:T,并将其输入SNN解码器以生成图像![]() 。
。
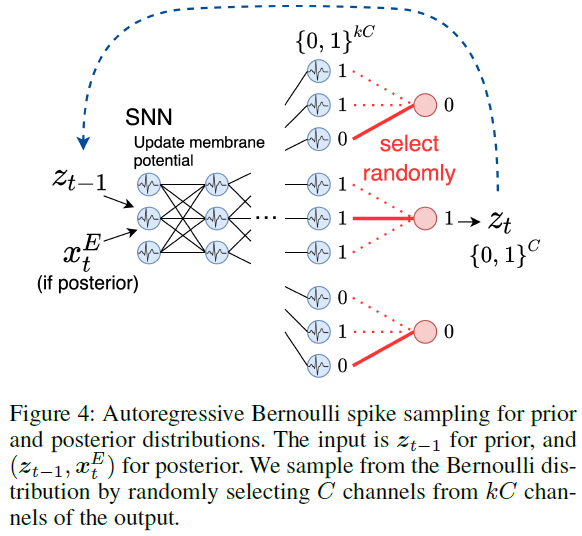
Autoregressive Bernoulli Spike Sampling
我们定义后验概率和先验概率分布如下:
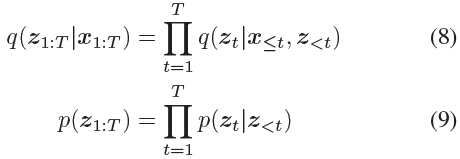
我们需要用SNN对q(zt|x≤t, z<t)和p(zt|z<t)进行建模。值得注意的是,所有SNN特征必须是二值时间序列数据。因此,我们不能像传统VAE那样使用重参数化技巧从正态分布中采样。
因此,我们将q(zt|x≤t, z<t)和p(zt|z<t)定义为采用二值的伯努利分布。首先,我们需要从z<t中顺序生成zt;因此,我们使用自回归SNN模型。通过从其输出中逐个随机选择,我们可以从伯努利分布中进行采样。此采样方法的概述如图4所示。
当q(zt|x≤t, z<t)的自回归SNN模型为fq,p(zt|z<t)为fp时,它们的输出如下:
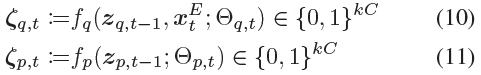
其中C是zt的维数,k是从2开始的自然数。![]() 是编码器的输出。Θq,t和Θp,t是fq和fp中神经元的膜电位集合,由输入更新。
是编码器的输出。Θq,t和Θp,t是fq和fp中神经元的膜电位集合,由输入更新。
通过为每个k值随机选择一个来执行采样:
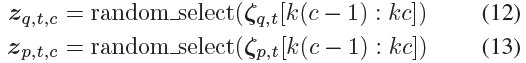
通过在1≤c≤C中这样做,我们可以采样zq,t, zp,t ∈ {0, 1}C。
在神经形态设备之一TrueNorth中,存在一种伪随机数生成器机制,可以随机替换突触权重(Wen等人,2016),这使得这种采样方法可行。
这相当于从以下伯努利分布中取样:
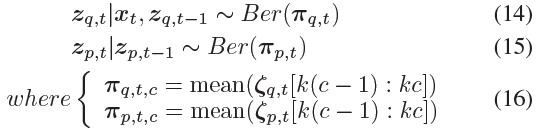
因此,
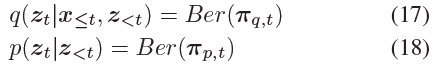
Spike to Image Decoding using Membrane Potential
采样的zt被顺序地输入到SNN解码器,SNN解码器输出脉冲序列。我们需要将其解码为重建图像![]() 。为了利用SNN的框架,我们使用输出神经元的膜电位进行脉冲到图像解码。我们在输出层中使用非发放神经元,并通过测量最后一次T时的膜电位将
。为了利用SNN的框架,我们使用输出神经元的膜电位进行脉冲到图像解码。我们在输出层中使用非发放神经元,并通过测量最后一次T时的膜电位将![]() 转换为实际值。公式(2)如下所示:
转换为实际值。公式(2)如下所示:
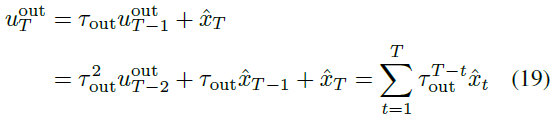
我们开始τout=0.8,并获得实值重建图像为![]() 。
。
Loss Function
ELBO如下:
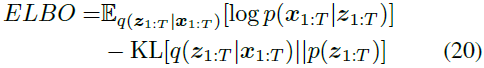
第一项是重建损失,它是![]() ,与通常的VAE一样。第二项,KL散度,表示先验概率分布和后验概率分布的接近程度。传统VAE使用KL散度,但我们使用MMD,这已被证明是MMD-GLM中脉冲序列的更合适的距离度量(Arribas、Zhao和Park 2020)。MMD可以使用核函数k编写如下:
,与通常的VAE一样。第二项,KL散度,表示先验概率分布和后验概率分布的接近程度。传统VAE使用KL散度,但我们使用MMD,这已被证明是MMD-GLM中脉冲序列的更合适的距离度量(Arribas、Zhao和Park 2020)。MMD可以使用核函数k编写如下:
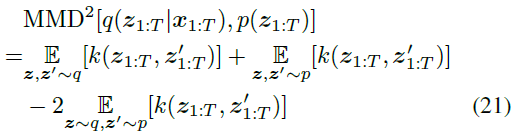
我们将![]() 设置为MMD-GLM中基于模型的核。PSP代表突触后电位函数,可以捕捉脉冲序列的时间序列性质(Zenke和Ganguli 2018)。我们使用一阶突触模型(Zhang和Li 2020)作为PSP。以下更新公式用于计算PSP(z≤t):
设置为MMD-GLM中基于模型的核。PSP代表突触后电位函数,可以捕捉脉冲序列的时间序列性质(Zenke和Ganguli 2018)。我们使用一阶突触模型(Zhang和Li 2020)作为PSP。以下更新公式用于计算PSP(z≤t):
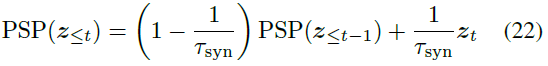
其中τsyn是突触时间常数。我们将PSP(z≤0)设置为0。
这给出了等式(21),如下所示。详细推导见补充材料B。
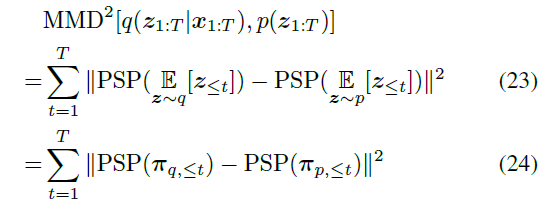
损失函数计算如下:
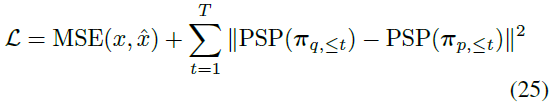
Experiments
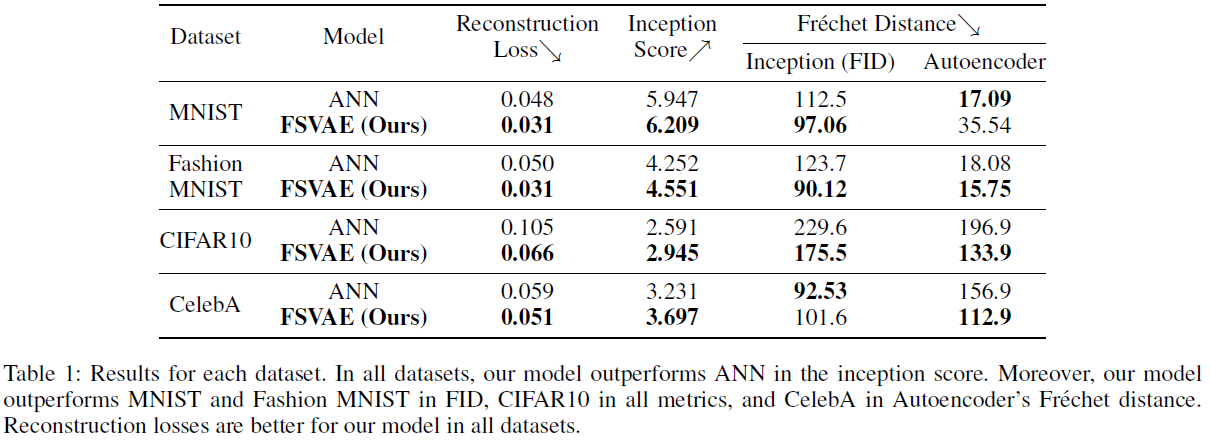
我们在PyTorch中实现了FSVAE(Paszke等人,2019),并使用MNIST、Fashion MNIST,CIFAR10和CelebA对其进行了评估。结果汇总在表1中。
Datasets
对于MNIST和Fashion MNIST,我们使用了60000张图像进行训练,10000张图像进行评估。输入图像的大小调整为32x32。对于CIFAR10,我们使用了50000张图像进行训练,10000张图像进行评估。对于CelebA,我们使用162770张图像进行训练,使用19962张图像进行评估。输入图像的大小调整为64x64。

Network Architecture
SNN编码器包括几个卷积层,每个卷积层的核大小为3,步长为2。MNIST、Fashion MNIST和CIFAR10的层数为4,CelebA的层数为5。在每一层之后,我们设置了tdBN(Zheng等人。2021),然后将该特征输入LIF神经元以获得输出脉冲序列。编码器的输出为![]() ∈{0, 1}C,潜在维度C=128。我们将其与zt-1∈{0, 1}C结合,并将其输入到后验模型;因此,其输入维度为128+128=256。此外,我们设置z0=0。后验模型包括三个FC层,并将信道数量增加了k=20。zt通过提出的自回归伯努利脉冲采样从中采样。我们重复这个过程T=16次。现有模型具有相同的模型架构;然而,由于输入仅为zt-1,其输入维度为128。
∈{0, 1}C,潜在维度C=128。我们将其与zt-1∈{0, 1}C结合,并将其输入到后验模型;因此,其输入维度为128+128=256。此外,我们设置z0=0。后验模型包括三个FC层,并将信道数量增加了k=20。zt通过提出的自回归伯努利脉冲采样从中采样。我们重复这个过程T=16次。现有模型具有相同的模型架构;然而,由于输入仅为zt-1,其输入维度为128。
采样的zt被输入到SNN解码器,该解码器包含与编码器相同数量的反卷积层。解码器的输出是与输入相同大小的脉冲序列。最后,根据等式(19),我们执行脉冲到图像解码以获得重建图像。
Training Settings
我们使用AdamW优化器(Loshchilov和Hutter 2019),该优化器训练150个回合,学习率为0.001,权重衰减为0.001。批大小为250。在先验模型中,教师强迫(teacher forcing,Williams和Zipser 1989)用于稳定训练,因此先验的输入为zq,t,其从后验模型采样。此外,为了防止后验塌陷,进行了计划取样(scheduled sampling,Bengio等人,2015)。在一定概率下,我们输入zp,t而不是zq,t。该概率在训练期间从0到0.3线性变化。
Evaluation Metrics
采样图像的质量通过初始得分(inception score,Salimans等人,2016年)和FID(Heusel等人,2017年;Parmar、Zhang和Zhu,2021)进行测量。然而,由于FID考虑到ImageNet预训练初始模型的输出,它可能无法在MNIST等数据集上很好地工作,因为MNIST与ImageNet具有不同的域。因此,我们事先在每个数据集上训练了一个自动编码器,并使用它来测量采样图像和真实图像之间的自动编码器潜在变量的Fréchet距离。我们采样了5000张图像来测量距离。作为一种比较方法,我们准备了使用ANN构建的相同网络架构的普通VAE,并在相同的设置下进行训练。
表1显示,我们的FSVAE在所有数据集的初始得分上都优于ANN。对于MNIST和Fashion MNIST,我们的模型在FID、CIFAR10的所有指标以及CelebA的预训练自动编码器的Fréchet距离方面都更优。由于SNN只能使用二值,因此很难执行复杂的任务;相反,我们的FSVAE在图像生成中获得了与ANN相同或更高的分数。
Computational Cost 我们测量了推断单个图像需要多少浮点加法和乘法。我们将结果汇总在表2中。ANN的加法次数减少了6.8倍,但SNN的乘法次数减少了14.8倍。一般来说,乘法比加法更昂贵,因此乘法次数更少更可取。此外,当在神经形态设备中实现SNN时,SNN预计比ANN快约100倍,因此FSVAE在速度方面可以显著优于ANN VAE。
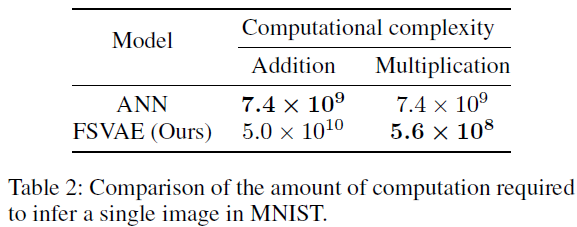
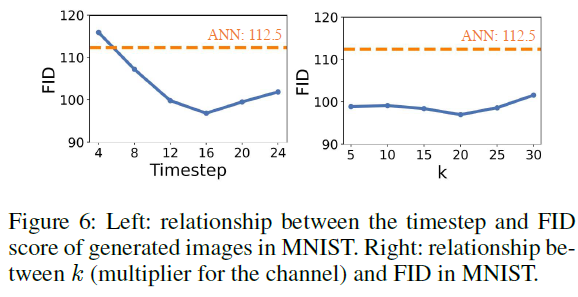
图6显示了FID随时间步长和k(输出选择的数量)的变化。当时间步长为16时获得最佳FID。少量时间步长没有足够的表达能力,而大量时间步长使潜在空间过大;因此,最佳时间步长被确定为16。此外,FID随k变化不大,但当k=20时最佳。
Ablation Study 结果汇总在表3中。计算KLD时,πq,t和πp,t加上ε=0.01以避免发散。使用MMD作为损失函数并将PSP应用于其核,获得最佳FID分数。

Qualitative Evaluation
图5显示了生成的图像的示例。在CIFAR10和Fashion MNIST中,ANN VAE生成模糊和模糊的图像,而我们的FSVAE生成更清晰的图像。在CelebA中,FSVAE生成的图像具有比ANN更清晰的背景区域。这是因为FSVAE的潜在变量是离散的脉冲序列,因此它可以避免后崩溃,如VQ-VAE(van den Oord、Vinyals和Kavukcuoglu 2017)。
图7显示了Fashion MNIST的重建图像。FSVAE比ANN更清晰地重建图像,尤其是细节。这是因为FSVAE的潜在变量是离散的。解码器忽略潜在变量会导致后验塌陷。对于离散的潜在变量,每个潜在变量都变得有意义,这可以防止后验崩溃。

Conclusion
在这项研究中,我们提出了FSVAE,它允许在SNN上生成与ANN相同或更高质量的图像。我们提出了自回归伯努利脉冲采样,这是一种可以在神经形态设备上实现的脉冲采样策略。这种采样方法用于先验分布和后验分布,我们将隐脉冲序列建模为伯努利过程。在多个数据集上的实验表明,FSVAE可以生成与相同架构的ANN VAE相同或更高质量的图像。由于SNN在神经形态设备上的速度明显更快,因此FSVAE在速度方面可以显著优于ANN VAE。将来,当我们结合最近的VAE研究时,我们很快就能用SNN实现高分辨率图像生成。
Supplementary Material
A Network Architecture
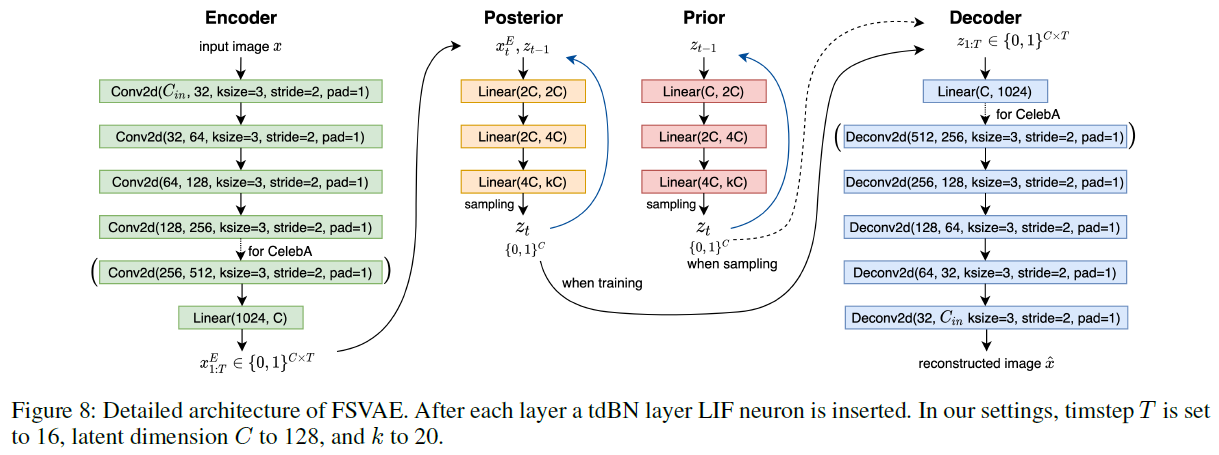
图8显示了FSVAE的详细架构。对于CelebA数据集,我们为编码器和解码器添加了一个附加层。ANN VAE的结构与FSVAE相同,除了前向和后向。
B Derivation of MMD

C Derivation of KLD
在消融研究中,我们使用KLD作为前后分布之间的距离度量。KLD计算如下:
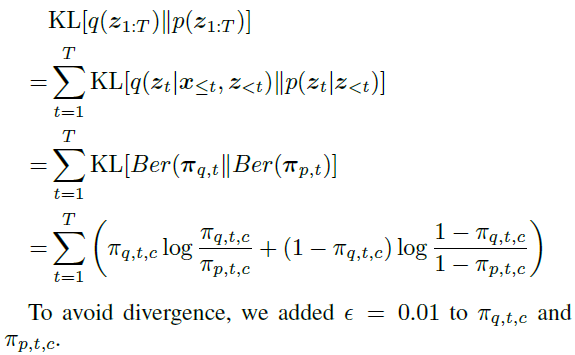
D Analysis of Spike Activities
图9显示了输入图像及其对应的潜在脉冲序列。可以看出,一些脉冲序列更具周期性,而另一些则更具爆发性。这种多样性允许脉冲序列对各种不同的图像进行编码。
图10显示了每层的平均发放率。每个发放率都是稳定的,有助于稳定的学习。

E Codes for Algorithms
我们在算法1中展示了用于后验的自回归伯努利脉冲采样的详细代码,在算法2中展示了先验。此外,算法3展示了整体训练和采样过程。







 浙公网安备 33010602011771号
浙公网安备 33010602011771号