Training Feedback Spiking Neural Networks by Implicit Differentiation on the Equilibrium State

郑重声明：原文参见标题，如有侵权，请联系作者，将会撤销发布！

35th Conference on Neural Information Processing Systems (NeurIPS 2021).

 

Abstract

　　脉冲神经网络(SNN)是受大脑启发的模型，可在神经形态硬件上实现节能实现。然而，由于脉冲神经元模型的不连续性，SNN的监督训练仍然是一个难题。大多数现有方法模仿人工神经网络的反向传播框架和前馈架构，并使用替代导数或计算关于脉冲时间的梯度来处理问题。这些方法要么累积近似误差，要么仅通过现有脉冲有限地传播信息，并且通常需要沿时间步骤传播信息，并且具有较大的内存成本和生物学不合理性。在这项工作中，我们考虑了更像大脑的反馈脉冲神经网络，并提出了一种新的训练方法，它不依赖于前向计算的精确反向。首先，我们表明具有反馈连接的SNN的平均发放率会随着时间逐渐演化到平衡状态，这遵循一个不动点方程。然后通过将反馈SNN的前向计算视为该方程的黑盒求解器，并利用方程的隐式微分，我们可以计算参数的梯度，而无需考虑精确的前向过程。通过这种方式，前向和后向过程是解耦的，因此避免了不可微的脉冲函数的问题。我们还简要讨论了隐微分的生物学合理性，它只需要计算另一个平衡。在MNIST、Fashion-MNIST、N-MNIST、CIFAR-10和CIFAR-100上的大量实验证明了我们的方法在少量时间步长内具有较少神经元和参数的反馈模型的卓越性能。我们的代码可从https://github.com/pkuxmq/IDE-FSNN获得。

 

1 Introduction

　　脉冲神经网络(SNN)由于其固有的高能效计算，最近受到越来越多的关注[22, 41, 44, 36, 8]。受人脑中神经元的启发，生物学合理的SNN在神经元之间传输脉冲信号，从而实现基于事件的计算，该计算可以在能耗更低的神经形态芯片上进行[1, 7, 33, 36]。同时，从理论上讲，SNN在计算上比人工神经网络(ANN)更强大，因此被视为第三代神经网络模型[25]。

　　尽管有这些优点，但SNN的直接监督训练仍然是一个难题，与流行的ANN相比，这阻碍了SNN的实际应用。主要障碍在于复杂的脉冲神经元模型。虽然反向传播[38]对ANN效果很好，但它受到脉冲生成的不连续性的影响，这在SNN训练中是不可微的。最近成功的SNN训练方法仍然通过沿时间步骤展开的计算图的误差传播来模仿反向传播(BPTT)[42]框架，并且它们通过应用替代导数来逼近梯度来处理脉冲函数[44, 5, 15, 41, 45, 29, 17, 50]，或者通过计算仅在脉冲神经元上相对于脉冲时间的梯度[6, 49, 17]。然而，这些方法要么沿时间步骤累积近似误差，要么遭受"死神经元"问题[41]，即当没有神经元脉冲时学习不会发生。同时，BPTT需要记住所有时间步骤的中间变量并沿它们进行反向传播，这会消耗内存并且在生物学上是不合理的。因此，有必要考虑沿着更适合SNN的计算图进行反向传播以外的训练方法。

　　另一方面，最近的SNN模型只是简单地模仿了ANN的前馈架构[44, 41, 45, 49, 50]，它忽略了人脑中无处不在的反馈连接。反馈(循环)电路对于人类用于目标识别的视觉系统至关重要[16]。同时，[19]表明，与深度ANN相比，具有递归性的浅层ANN在大规模视觉识别任务上实现了更高的人脑功能合理性和类似的高性能。因此，结合反馈连接可以使神经网络更浅、更高效、更像大脑。至于SNN，反馈在早期模型中很流行，例如液体状态机[26]，它利用具有固定权重或通过无监督方法训练的循环储藏层。与ANN通过沿时间展开来合并反馈连接的不经济成本相比，SNN自然地使用多个时间步骤进行计算，这本身就支持反馈连接。大多数最近的SNN模型模仿前馈架构，因为它们曾经缺乏有效的训练方法，因此它们借鉴了成功的ANN的一切。我们专注于另一个方向，即反馈SNN，这也是视觉任务的自然选择。

　　在这项工作中，我们考虑了反馈脉冲神经网络(FSNN)的训练，并提出了一种基于平衡状态(IDE)的隐式微分的新方法。受隐式模型[3, 4]的最新进展启发，这些模型将权重绑定ANN视为求解不动点均衡方程并提出由该方程定义的替代隐式模型，我们推导出当平均输入收敛到均衡时，FSNN的平均发放率会随着时间逐渐演化到平衡状态，这也遵循不动点方程。然后我们将FSNN的前向计算视为不动点方程的黑盒求解器，并借用隐式模型[3, 4]中隐微分的思想来计算梯度，它只依赖于方程而不依赖于确切的前向过程。这样，梯度计算与SNN中的脉冲函数无关，从而避免了SNN训练中常见的困难。虽然隐性微分似乎太抽象而无法在大脑中计算，但我们简要讨论了生物学合理性，并表明它只需要沿着神经元的反向连接计算另一个平衡。此外，我们将多层结构纳入反馈模型以获得更好的表征能力。我们的贡献包括：

• 我们是第一个在连续和离散视角下使用(L)IF模型从FSNN的平均发放率的不动点方程理论上推导出平衡状态的人。据此，FSNN的前向计算可以解释为求解一个不动点方程。
• 我们提出了一种基于平衡状态隐微分的FSNN新训练方法，该方法与前向计算图解耦并避免了SNN训练问题，例如不可微性和大内存成本。我们还讨论了生物学合理性并证明了与赫布学习规则的联系。
• 我们对MNIST、Fashion-MNIST、N-MNIST、CIFAR-10和CIFAR-100进行了广泛的实验，这证明了我们的方法在静态图像和神经形态输入的少量时间步骤内使用较少神经元和参数的优异结果。特别是，我们直接训练的模型在复杂的CIFAR-100数据集上只需30个时间步骤就可以超越最先进的SNN性能。

 

2 Related Work

Training Methods for Spiking Neural Networks.

 

Equilibrium of Neural Networks.

 

3 Preliminaries

3.1 Spiking Neural Network Models

 

3.2 Implicit Differentiation on the Fixed-Point Equation

 

4 Proposed IDE Method

　　在本节中，我们首先推导FSNN在连续和离散视图下的平衡状态，并证明FSNN可以被视为求解不动点方程。然后我们介绍了如何通过基于方程的所提出的IDE方法来训练网络，并简要讨论了生物学的合理性。最后，我们在模型中加入了多层结构，以获得更多的非线性和更强的表示能力。

 

4.1 Derivation of Equilibrium States for Feedback Spiking Neural Networks

4.1.1 Continuous View

 

4.1.2 Discrete View

 

4.2 Training of Feedback Spiking Neural Networks

　　基于第4.1节的推导，我们可以将FSNN的前向计算视为不动点平衡方程的黑盒求解器，存在一些由有限时间步骤或LIF模型引起的误差。然后我们假设 T 个时间步骤后的(加权)平均发放率a[T]大致遵循公式。我们将演示如何训练FSNN及其生物学合理性。

 

4.2.1 Loss and Gradient Computation

　　假设我们通过 T 个时间步骤来模拟SNN。令a[T]表示最终(加权)平均发放率。我们在这些脉冲神经元之后配置了一个读出层，它作为一个全连接的分类层，输出的量作为类号。我们假设这些神经元不会发放脉冲或重置，并根据累积的膜电位进行分类*。然后输出等价于a[T]上的线性变换，即o = W^oa[T]。损失 L 由常用损失函数L(o, y)在 o 和标签 y 上定义，我们利用了交叉熵损失。

　　令 f_θ 表示不动点方程中的函数，例如。参数的梯度可以根据3.2节中描述的隐式微分计算，方法是将 a* 替换为a[T]。然后可以基于常见的梯度下降方法优化参数，例如SGD [38]及其变体。附录B中提供了一个伪代码。

 

* 在代码实现中，直接使用一个全连接的MLP作为分类器。

 

4.2.2 Biological Plausibility of Implicit Differentiation

 

4.3 Incorporating Multi-layer Structure into The Feedback Model

 

5 Experiments

　　在本节中，我们进行了广泛的实验来证明我们提出的方法的优越性能。请参阅附录 F 了解实现细节，包括对频谱范数和批归一化的限制，以及训练参数。由于以前很少有方法利用反馈架构，因此我们将FSNN的IDE方法的结果与大多数前馈SNN和报告网络结构²以及计算期间的神经元数量和参数(根据论文或发布的代码计算)进行比较。

 

² 符号是：'64C5'表示具有64个输出通道且核大小为5的卷积，'64C5'之后的's'表示步幅为2的卷积，而之后的'u'表示转置卷积到upscale 2×，'P2'表示大小为2的平均池化，'400'表示全连接到400个神经元，'F'表示反馈层。

 

5.1 MNIST and Fashion-MNIST

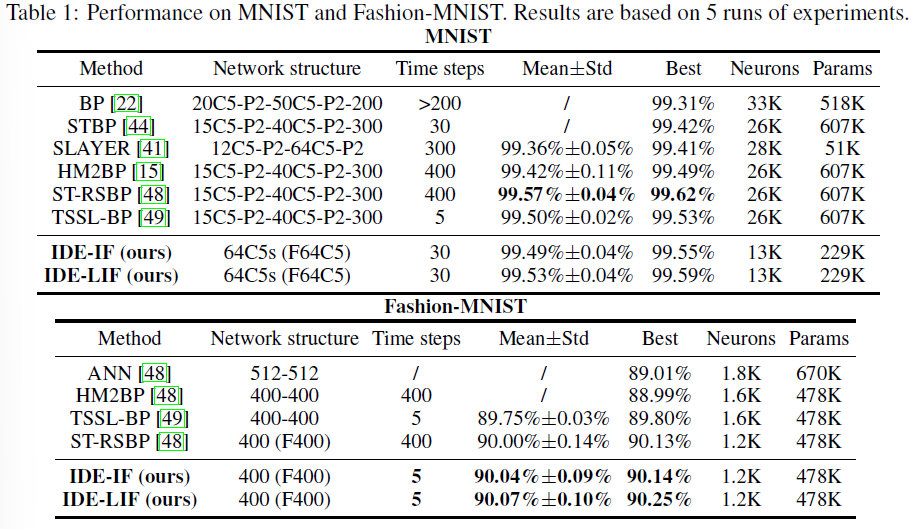
　　我们首先在简单的静态图像数据集(包括MNIST [20]和FashionMNIST [46])上评估我们的方法，并将结果与​​其他直接训练的SNN [22, 44, 41, 15, 48, 49]或类似的ANN进行比较。输入是在所有时间步骤上具有二值或实值的相同图像，可以视为输入电流[49]。我们利用单层FSNN，并在MNIST中采用卷积层，同时遵循[48]在Fashion-MNIST中使用全连接层。如表1所示，与前馈或反馈架构上的其他直接SNN训练方法相比，我们的模型在相对较少的时间步骤内以较少的神经元和参数实现了相当或更好的结果。特别是，我们的模型在具有相似结构的Fashion-MNIST上仅用5个时间步骤就取得了优异的结果。LIF模型的性能略好于IF模型，可能是因为它通过编码加权平均发放率来利用时序信息。

 

5.2 N-MNIST

 

5.3 CIFAR-10 and CIFAR-100

 

5.4 Convergence to the Equilibrium

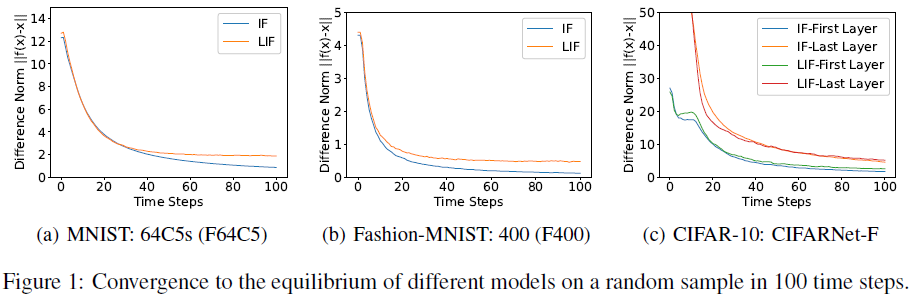
　　为了验证FSNN收敛到平衡状态，我们在每个时间步骤的不动点方程上绘制差分范数，即||f_θ(a[t]) - a[t]||，其中x = f_θ(x)是不动点方程，并且a[t]是时间步骤 t 的(加权)平均发放率。图1展示了不同模型的收敛性。不同样本之间几乎相同。由于发放率的数值精度仅为1/t ，由于时间步骤有限，会存在一定的收敛误差。并且对于LIF模型，与IF模型相比可能存在随机误差，如第4节所示。随着差分范数逐渐减小，结果符合定理，即发放率收敛到方程后的平衡。它还表明精确的精度对于令人满意的性能不是必需的。神经元较少的网络收敛速度更快，因此需要较少的时间步数，这解释了为什么在Fashion-MNIST实验中只有5个时间步骤就足够了。有关更多数据集和不同时间步长的结果，请参阅附录G。

 

5.5 Training Memory Costs

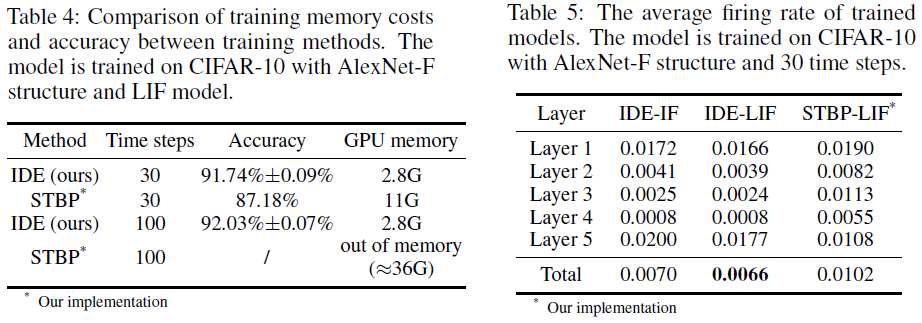
　　如引言中所述，我们方法的一个重要优点是我们可以避免大内存成本，沿计算图反向传播的方法会受到影响。为了量化这种训练的便利性，我们比较了我们的方法和代表性STBP方法的GPU内存成本[44, 45]。架构和训练设置相同，结果如表4所示。它很好地说明了我们方法的较小内存成本，这也与时间步长无关。同时，我们的方法可以获得更高的性能。

 

5.6 Firing Sparsity

　　至于有效的神经形态计算，发放率是一个重要的统计数据，因为能量消耗与脉冲的数量成正比。我们计算训练模型的平均发放率，并比较我们的IDE方法训练的IF和LIF模型，以及具有相同结构的STBP方法[44, 45]训练的LIF模型。表5中的结果证明了我们模型的发放稀疏性，因为平均发放率仅为0.7%左右或低于0.7%。并且它表明LIF模型与IF模型相比具有稍微稀疏的响应。我们注意到TSSL-BP [49]还报告了关于发放率的统计数据。根据他们的结果，他们在CIFAR-10上训练的模型在5个时间步骤内的总发放率大约为9.86%。因此有趣的是，即使我们有更多的时间步骤(30对5)，我们的模型也比他们的模型有更少的脉冲，更不用说我们的模型有更少的神经元。结果还表明，与STBP相比，我们方法训练的模型具有更稀疏的脉冲，证明了我们方法的优越性。

 

6 Conclusion

　　在这项工作中，我们提出了一种基于平衡状态隐式微分的反馈脉冲神经网络的新训练方法。我们首先推导出FSNN的IF和LIF模型在连续和离散视图下的(加权)平均发放率的平衡状态。然后，我们建议仅基于底层不动点方程的隐式微分来优化FSNN的参数。这使得后向过程能够与前向计算图解耦，因此避免了SNN的常见训练问题，例如不可微分性和大内存成本。同时，我们简要讨论了计算隐式微分的生物学合理性，它只需要计算另一个平衡点，并且与局部更新的赫布学习规则有关。大量实验证明了我们的方法和模型在少量时间步内具有更少的神经元和参数的优异结果，并且在我们训练的模型中脉冲也更稀疏。