Integrating Non-spiking Interneurons in Spiking Neural Networks
郑重声明:原文参见标题,如有侵权,请联系作者,将会撤销发布

Frontiers in neuroscience, (2021): 633945-633945
Abstract
研究神经网络的研究人员历来专注于可在计算机上运行的非脉冲神经元或通常需要特殊硬件的更具生物学意义的脉冲神经元。然而,自然界中不存在同质的神经元网络。相反,脉冲和非脉冲神经元合作,各自带来不同的优势。这种混合网络的一个经过充分研究的生物学例子是感觉运动通路,负责将感觉输入映射到行为变化。这种类型的路径在机器人技术中也得到了很好的研究,通过调整电机输出的幅度、频率和相位,它被应用于实现有腿机器人的闭环操作。在本文中,我们研究了脉冲和非脉冲神经元如何组合以创建能够基于模拟输入塑造网络输出的感觉运动神经元通路。我们提出对现有脉冲神经元模型进行亚阈值操作,以创建能够解释模拟信息并与脉冲神经元通信的非脉冲神经元。该方法的有效性通过模拟闭环幅度调节网络得到证实,该网络受昆虫中发现的用于姿势的内部反馈回路的启发。此外,我们表明非脉冲神经元可以在基于事件的架构中有效地操纵突触后脉冲神经元。使用混合网络的能力为研究人员研究自适应控制器的新网络架构提供了机会,有可能改善有腿机器人的运动策略。
Keywords: spiking neural network, non-spiking interneuron, neuromorphic engineering, mixed network, biologically plausible neuron, bio-inspired engineering
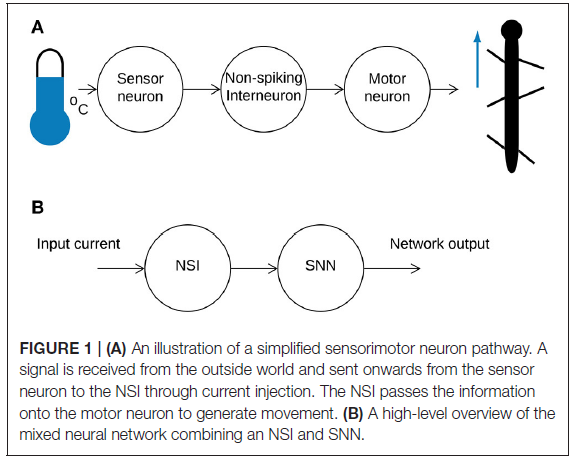
1. INTRODUCTION
目前使用神经网络进行运动控制的研究往往侧重于通过分级信号(Aoi et al., 2017)或动作电位(Bing et al., 2018)进行通信的神经元的同质网络。然而,研究表明生物神经网络利用两种通信策略(Burrows, 1996)来实现有效的运动。基于此,我们的研究将受生物学启发的非脉冲中间神经元(NSI)模型引入脉冲神经网络(SNN),以进一步提高生物保真度。在自然界中,传感器神经元从外部环境接收信息,并通过电流注入将其传递给NSI (Bidaye et al., 2018)。该数据由NSI继续发送,通过分级信号影响连接神经元的膜电位(Burrows and Siegler, 1978)。然而,NSI不仅仅是转换单元。它们还被发现是某些动物的主要神经元类型,例如线虫,其中通过分级电位进行交流是主要的传输方法(Schafer, 2016)。因此,中间神经元本身就是计算单元。图1说明了一个简化的神经通路,描绘了来自环境产生的昆虫运动的模拟输入(图1A)和本研究中实现的等效通路(图1B)。
可以使用不同的模型来描述单个神经元,这些模型试图捕捉生物神经元的动态。在这项研究中,我们使用了两个脉冲神经元模型,一个以其预期的方式工作,而另一个在其亚阈值范围内运行,因此膜电位永远不会超过脉冲阈值。脉冲神经元模型试图通过在每个时间步骤计算神经元的膜电位来复制生物神经元。膜电位受传入脉冲、偏置电流和其他参数的影响,具体取决于模型的方程。人工神经网络(ANN)中使用的经典非脉冲神经元模型尝试使用传递函数(例如sigmoid函数)来复制神经元动态。这些非脉冲模型能够映射值,但它们无法在没有循环连接的情况下随着时间的推移整合输入。因此,我们的论文在非脉冲"模式"中使用脉冲神经元模型来创建NSI。
SNN通常通过被称为脉冲的动作电位进行通信。脉冲允许通过脉冲频率以及单个脉冲的时间对信息进行编码(Bohte, 2004)。与传统ANN相比,这创造了在脉冲序列内传输更多信息的可能性(Bing et al., 2018)。我们的研究中使用了SNN,因此未来结合数据丰富的感官输入的工作可以利用时间特征来编码输入信息。
由于SNN通常是同质的,因此所有通信都是通过在神经元之间传递脉冲来处理的。如果将模拟传感器添加到网络中,则必须将信息编码为脉冲信号以供网络理解。对于必须从脉冲转换为连续值以控制电机的输出信号也是如此。在自然界中发现的已知编码机制包括个体脉冲发放率(Adrian, 1926)、群体活动(Panzeri et al., 2015)和精确的脉冲时间(Bohte, 2004)。神经网络工程师已经应用了这些方法中的每一种来转换感觉输入,将不同的方法分别分为三个主要类别:发放率、群体和时序编码。
每个编码类别都有公认的优势。与单个神经元相比,群体编码能够传递更多信息,因此对于数据丰富的输入很有用(Mallot, 2013)。另一方面,时序编码特别适用于编码流数据,因为它可以快速处理信息(Petro et al., 2019),同时最大化压缩数据中包含的信息量(Sengupta and Kasabov, 2017)。最后,虽然其他方法能够编码更多信息,但发放率编码被认为是处理高发放率输入的最佳工具(Azarfar et al., 2018)。在我们的工作中,发放率编码用于将网络的输出从脉冲信号过滤为连续的运动信号,并且我们引入了NSI模型作为一种混合编码方法,能够自行直接转换输入或与发放率、群体或时间一起工作以增加编码信息量的方法。
1.1. Related Work
ANN已被证明可以有效地操纵有腿机器人的振幅、频率和相位以创建自适应控制器(Nachstedt et al., 2013; Schilling et al., 2013; Barikhan et al., 2014; Dürr et al., 2019; Pitchai et al., 2019; Thor and Manoonpong, 2019)。Thor and Manoonpong (2019)使用误差信号更新突触权重以适应频率以优化步行,从而提高效率并减少跟踪误差。Pitchai et al. (2019)还通过使用ANN来塑造网络输出以及非脉冲中央模式发生器(nCPG)来改变频率,从而为腿式机器人创建了一种节能控制机制。Nachstedt et al. (2013)能够使用自适应振荡器创建一个自调整网络,允许机器人在更复杂的环境中导航。Barikhan et al. (2014)表明,使用感官反馈来适应环境的解耦nCPG网络能够处理机器人形态的变化,并且在执行协作任务时可以与另一个机器人协调运动。Schilling et al. (2013)使用协调规则根据感官输入来适应步行。同样,Dürr et al. (2019)开发了一种ANN来控制六足机器人,该机器人依靠姿势反馈和协调规则。他们的网络产生新兴的步态,根据机器人的姿势进行调整。Szczecinski et al. (2015)研究了向ANN中添加非脉冲中间神经元。他们报告了使用模拟为经典非脉冲神经元的中间神经元来触发不同的生物启发反射来控制六足机器人。中间神经元用于控制输出振荡,表明通过中间神经元塑造nCPG输出以重现生物行为是可能的。我们的论文结合使用NSI和脉冲神经元来更新振幅、频率和相位,作为创建能够解释时间数据的更具生物学合理性的自适应控制器的一步。
纯SNN还能够通过更新不同的突触和神经元特征来操纵输出幅度、频率和相位(Strohmer et al., 2020)。发现可以通过更新脉冲中央模式发生器(sCPG)神经元群的电压阈值电位值来改变频率,同时使用突触电导对运动神经元群(MNP)的权重增加或减小幅度。最后,相位由网络架构和突触延迟决定。然而,由于已知NSI的输入电流会改变连接的运动神经元的发放率、重置有规律的输出(Bidaye et al., 2018)和更新幅度(von Uckermann and Büschges, 2009),因此研究它们如何与sCPG网络交互以塑造这些输出。
Wozniak et al. (2020)将脉冲神经元集成到ANN中,以利用其节能潜力和时间数据编码功能。他们将脉冲神经元实现为由两个非脉冲神经元组成的"脉冲神经单元",其中一个处理膜电位的整合,另一个发出脉冲。脉冲神经单元动态是在脉冲神经元的LIF模型之后建模的。它们对膜电位的整合是通过循环连接处理的,同时使用阶跃函数模拟脉冲。这种方法不同于我们的实现,因为它将脉冲神经元定义为非脉冲神经元的组合,而我们采用脉冲神经元模型的动态并在亚阈值区域使用它来创建非脉冲神经元模型。
Patil et al. (2015)对我们的研究采取了类似的方法,并创建了一个非脉冲神经元,建模为通过分级电位进行通信的脉冲神经元。他们的工作基于线虫的神经结构,该结构主要由非脉冲神经元组成,尽管最近的研究表明蠕虫中更先进的感觉系统可能使用脉冲神经元(Liu et al., 2018)。该论文表明,可以构建一个混合神经网络来模拟线虫在被外部接触时的逃逸反应。他们的混合网络被实现为神经形态硬件,使用模拟电路模拟非脉冲和脉冲神经元,而不是我们使用模拟软件对神经元进行数学建模的研究。
Niu et al. (2017)使用在现场可编程门阵列上设计的神经形态硬件探索感觉运动回路的第一原理。他们能够在硬件中成功模拟脉冲神经元和肌肉生理学,以在附着的尸体手指和机器人手指中重现牵张反射。这项研究强化了一种预期,即感觉运动回路的简化模型会在解剖系统中产生逼真的行为。其他生物学研究调查中央模式生成器(CPG)本身的架构,使用多层CPG网络生成有规律的输出并在多个层上实现相互抑制(参见评论,McCrea and Rybak, 2008)。Markin et al. (2010)的CPG网络测试了下行信号的去除,并且能够通过增加与感觉反馈相关的突触权重来重新获得稳定的运动。相反,Danner et al. (2017)提出了一个依赖下降和上升信号来协调运动的网络。他们将中间神经元添加到他们的网络中,除了传递下降/上升信号外,还可以在腿之间进行通信,发现当某些中间神经元被移除时,某些步态模式是无法实现的。Mileusnic et al. (2006)的进一步工作提出了肌梭的数学模型,肌梭是负责关联肌肉长度和速度的感觉器官。该论文证实了重建生物数据的能力,提供了另一种研究感觉反馈在运动中的作用的方法。Raphael et al. (2010)扩展了这项研究,在他们的"类脊椎调节器"中使用肌梭模型,能够处理184个控制输入,使用下降输入和感觉反馈控制人手的近似值。我们的工作通过研究混合神经网络中的基本通信原理,整合了这项生物学研究的思想。
我们的论文提出了一种新颖的编码机制,即亚阈值编码,它使用NSI将来自模拟感官输入的值与SNN相关联。我们提出的方法被称为亚阈值编码,因为输出是低于脉冲阈值的膜电位波动的结果。与使用电流注入直接操纵网络输出相比,NSI的瞬时膜电位在突触后神经元如何受到影响方面发挥着作用。这项研究的主要贡献是介绍和研究如何将这些NSI集成到现有的SNN中以塑造网络输出。

2. METHODS
生物学研究表明,对NSI的感觉输入会影响运动输出(Büschges and Wolf, 1995)。此外,显示NSI接收到的去极化电流可以重置生物中枢模式发生器(bCPG)规律(Bidaye et al., 2018)。我们可以通过创建代表感觉运动神经元通路的等效神经网络来复制这些行为。在神经网络中,传感器神经元被NSI的输入偏置电流取代(见图1B),因此输入电流的变化代表来自外部环境的感觉信息的变化。然后NSI将此信息与连接的SNN相关联,以调整网络输出。图2B显示了所选SNN(一个sCPG网络)的框图。一对相互抑制的神经元群的结构基于驱动拮抗肌对的脉冲振荡器的生物学(Bidaye et al., 2018)。sCPG网络的输出是脉冲信号,但需要模拟信号来控制电机。因此,图2A演示了如何使用发放率编码将这些脉冲事件转换为模拟信号。这模拟了生物肌肉执行的低通滤波(Hooper et al., 2007),通过计算时间窗口内出现的脉冲数量来产生模拟值。图2C突出显示了由NSI输入调整的发放率编码输出的特性。
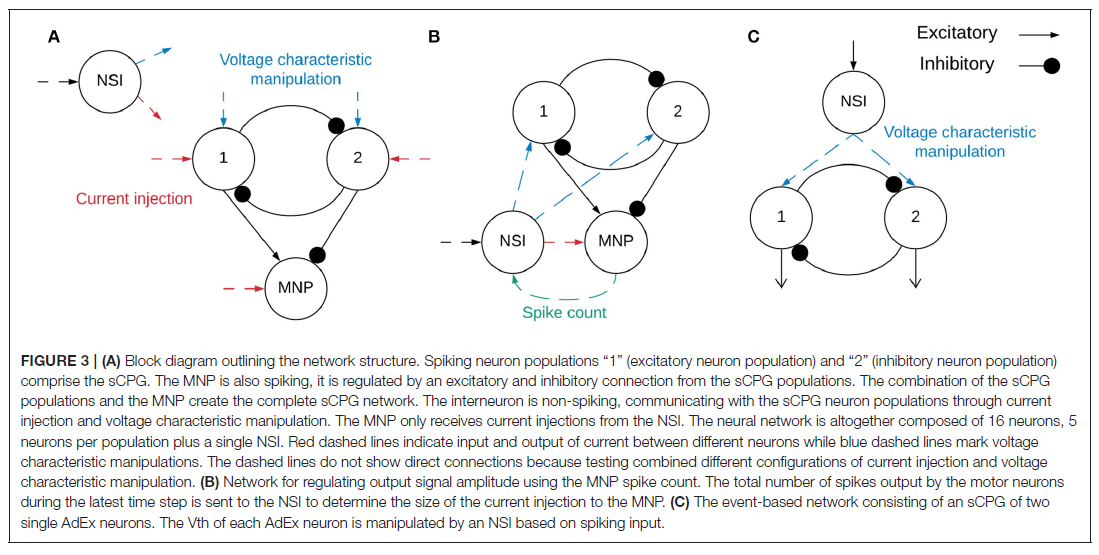
实施网络的示意图如图3A所示。该网络由一个NSI组成,该NSI能够注入电流并操纵突触后神经元的电压特性。
sCPG群体和MNP各由5个神经元组成,以便以最少的神经元产生平滑的输出(Strohmer et al., 2020)。NSI是单个神经元,因此与其相连的所有突触后神经元都接收相同的输入。这降低了实验的复杂性,因此测试的重点是来自NSI的通信。sCPG群体和MNP由自适应指数IF (AdEx)神经元组成,以允许bursting行为(Brette and Gerstner, 2005)。神经元参数是根据Naud et al. (2008)概述的规则突发设置的,其动态显示在公式(1)和(2)中。
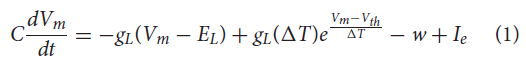
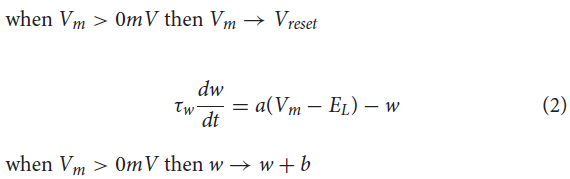
其中C是膜电容,Vm是膜电位,EL是静息电位,gL是泄漏电导,Ie是偏置电流加上高斯白噪声,a是亚阈值适应电导,b是脉冲触发适应,ΔT是锐度因子,τw是适应时间常数,Vth是电压阈值电位,Vreset是复位电位,w是脉冲适应电流(Naud et al., 2008)。公式(1)定义了每个时间步骤膜电位的变化,而公式(2)概述了当前的适应。
NSI被模拟为一个LIF神经元,神经元动态如公式(3)所示。脉冲阈值设置得足够高以避免脉冲,因此没有复位条件。NSI使用更简单的神经元模型,因为唯一必要的行为是输入电流和泄漏的积分。
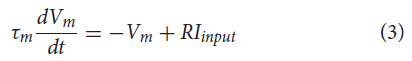
其中τm = RC是膜时间常数,Vm是膜电位,Iinput是输入偏置电流加上高斯白噪声,R是膜电阻。
Yang et al. (2013)表明NSI输出的大小是中间神经元膜电位与其静息电位之差的分级函数。此外,他们发现NSI产生的信号与突触后神经元的响应之间存在线性相关性。基于这些知识,我们构建了NSI膜电位与对突触后神经元的影响之间的关系(公式4和5)。
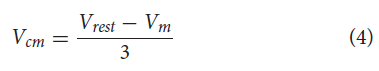
其中Vcm是电压特性操作,Vrest是静息电位,Vm是膜电位。
Vcm在网络中的应用在第2.1节概述实验中进一步描述。
公式(4)提供了针对sCPG神经元群调整的电压特性的偏移量。Vrest设置为-60mV以与生物学发现保持一致(Graubard, 1978)。Vrest的实际实施使用NSI膜电位的起始值,因为它由于系统中添加的噪声而在所需的静息电位附近波动。公式(4)中的除数将电压特性偏移限制在稳定范围内。它是通过将生物学上合理的15mV NSI膜电位波动范围(Burrows and Siegler, 1978)除以已知对sCPG网络稳定的5mV电压特性操作范围(Strohmer et al., 2020)来确定的。
公式(5)计算要添加到突触后神经元的原始电流偏置(Ie)中的电流量(Iinjection),以pA为单位。
![]()
其中Iinjection是电流注入,w是突触电导权重,Vrest是静息电位,Vm是膜电位。
突触电导权重w将电流从NSI注入到突触后神经元。电导以西门子(S)为单位,即欧姆的倒数(Ω-1)。
2.1. Time-Driven Experimentation
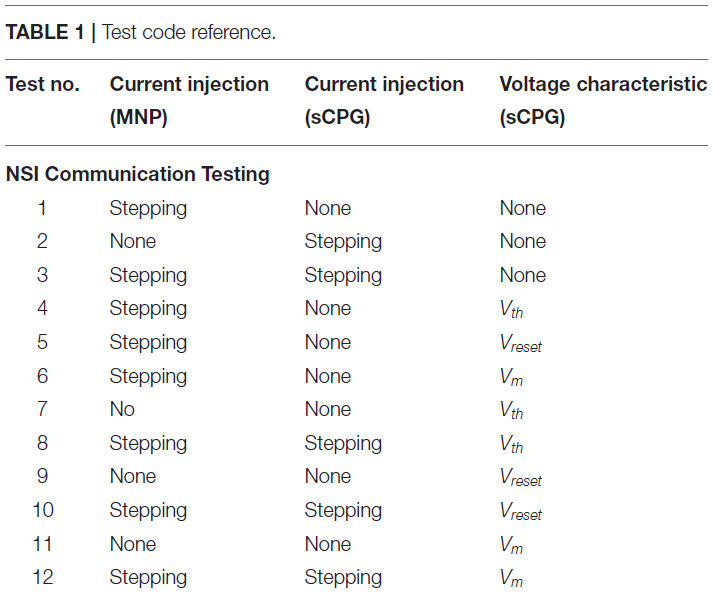
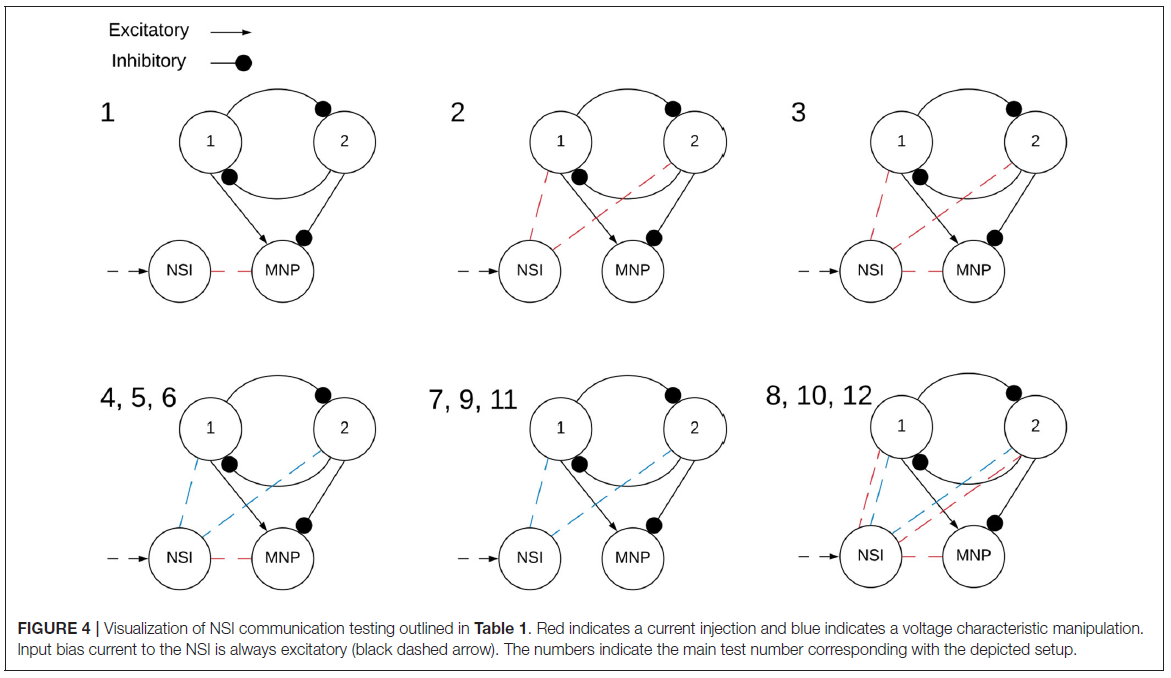
在网络上执行两大类测试,兴奋性和抑制性。NSI的输入偏置电流(Iinput)始终为正,这是公式(3)中定义的输入电流。然而,从NSI到突触后神经元的注入电流(Iinjection)会根据测试类型改变符号,如果兴奋则发送正电流,如果抑制则发送负电流。Iinjection的值由公式(5)确定。测试进一步分为NSI和突触后神经元群之间的相互作用。这些测试的概述在表1中进行了概述,并在图4中进行了可视化。
测试逐步通过注入电流和操纵突触后神经元群的电压特性的不同配置,如图4所示。电压特性测试分别研究调整公式(1)和(2)内的电压阈值电位(Vth)、电压复位(Vreset)和膜电位(Vm)。偏移量由电压特性操作公式(4)确定。由Vcm产生的偏移应用于被测试的单个特性。当Vcm被添加到神经元的膜电位(Vm)时,它会在计算公式(1)之后应用,从而允许Vcm在那个时间步骤直接添加到Vm。另一方面,当Vcm应用于Vth或Vreset时,它被添加到为每个设置的初始值。因此,当使用这些特性之一进行测试时,任一特性的实际值如下公式(6)和(7)所示。
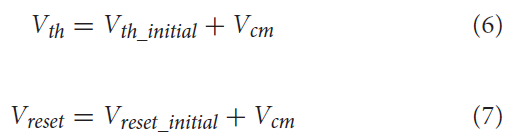
其中Vth_initial = -56mV和Vreset_initial = -41mV用于该特性的兴奋性测试;Vth_initial = -51mV和Vreset_initial = -46mV用于该特性的抑制测试。
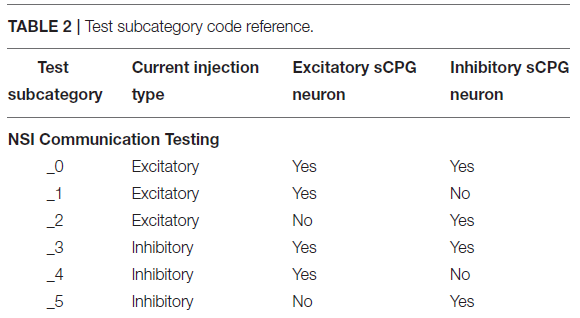
电压特性的操作中的每一个个别sCPG神经元群以及两者同时进行测试,这些是由表2所示并在图5可视化的测试子类别定义的。当一个测试正在运行不更新的特定电压特性,使用下列值:Vth = -51mV和Vreset = -46mV。已知这些值会通过sCPG网络产生规则的bursting模式(Strohmer et al., 2020)。MNP从不改变电压特性,因为它不涉及产生规律模式,仅塑造输出,它仅接收电流输入。
通过绘制MNP的发放率编码输出来比较测试结果。使用5ms的滑动时间窗口,计算每个时间窗口内发生的来自MNP的所有脉冲以产生模拟值。MNP的输出信号被视为网络的输出,因为这将是在物理机器人上进行测试时用于控制电机的信号。
首先执行静态Iinput测试以找到电导权重w的最大值(公式5)。这些静态测试未在上表中列出,因为它们仅用于参数调整。为了找到w,Iinput被设置为由NSI膜电位变化决定的最大值,将其限制在15mV的生物学合理范围内(Burrows and Siegler, 1978)。然后w以10nS的增量增加,直到找到最大权重。最大值被认为是产生理想输出信号的最大权重值,这将在第3节中进一步讨论。该值被设置为兴奋性和抑制性测试的最大电导权重(wmax)。发现这一点后,所有测试配置都会定期更新Iinput,以确认模拟输入的变化能够在线操纵网络输出。这些步进输入电流试验都使用wmax来计算公式(5)中的Iinjection。当测试为兴奋时,Iinput从0pA开始,以确定的最大值结束,当测试为抑制时则相反。这允许系统通过减少抑制来"兴奋",因此可以在输出端预期相同的一般行为。
Neural Simulation Tool (NEST) (Jordan et al., 2019)用于模拟网络并记录测试结果。对于所有试验,模拟运行6秒。NSI的输入电流每1秒更新一次,允许网络在初始瞬变之后在输入再次发生变化之前稳定下来。Iinput从0pA开始,到最大值148pA结束。因此,每一步都会增加29.6pA的输入电流。高斯白噪声电流被添加到网络中的所有神经元。NSI噪声电流的标准差设置为25pA,以便噪声电流与电流步长相当。当使用比这更大的值进行测试时,输出不再可靠地产生电压特性操作所需的偏移。对于所有其他神经元,标准差为50pA。噪声电流的标准差被选择并且没有被调整。bash脚本用于以可靠的方式运行测试。GitLab上提供了bash脚本和python测试脚本(请参阅数据可用性声明)。
在执行表1和2中概述的所有频率和幅度操作测试组合后,将执行进一步测试以查看输出相位如何受到频率之间切换的影响。频率要么保持恒定6秒,要么在4Hz和8Hz之间切换,每秒更新一次,持续6秒。为了检查仅受频率影响的相位,这些测试没有向电机群体注入电流。该测试不同于之前的sCPG网络相位操作,其中相位由突触延迟决定(Strohmer et al., 2020)。该试验并未尝试创建特定的相移,而是仅确认相位受频率变化的影响,并不试图对其进行控制。
昆虫使用本体感觉神经元来了解其四肢相对于身体的位置。这些内部反馈回路可以帮助昆虫进行抵抗反射以保持姿势(Tuthill and Wilson, 2016)。该知识用于实现模拟内部反馈回路(如图3B所示)的简化网络,作为概念应用的证明。MNP的发放率编码输出决定了连接NSI和MNP的突触的强度。进行了大量试验以确定用于兴奋性和抑制性权重计算的适当比例因子。
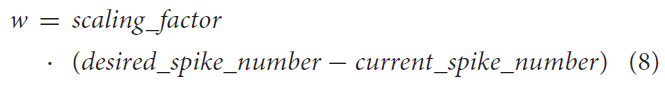
改变突触电导权重w将调节该内部反馈回路的输出幅度。公式(8)确定要在公式(5)中使用的w,而不是使用wmax。比例因子是一个允许最大效果而不会过度激励或过度抑制输出的值。所需的脉冲数作为设定点,而当前的脉冲数是来自MNP的实际脉冲数,发生在最后一个时间步骤。在这个网络中,如果时间窗口中的脉冲数量高于所需数量,则应用抑制权重,如果低于所需数量,则应用兴奋权重。

2.2. Event-Driven Experimentation
为了确认NSI与神经形态架构的兼容性,还在CloudBrain上模拟了网络 (Larsen et al., 2021)。CloudBrain是一个可扩展的基于事件的SNN模拟平台,利用事件流处理技术在作为集群上的微服务实现的神经元之间进行通信。CloudBrain 中的NSI实现为基于事件的泄漏积分器神经元,因此神经元模型可与NEST模拟相媲美。根据公式(9)中所示的动态,神经元在接收到输入事件后更新其膜电位。
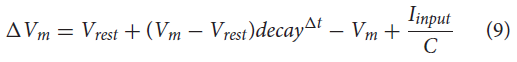
其中ΔVm是膜电位的变化,Vrest是静息电位,decay是模拟泄漏的衰减因子,dt是自上次传入脉冲以来的时间,Iinput是来自其他神经元的输入电流,C是膜电容。
公式(9)是时间驱动系统中公式(3)的事件驱动等价物。事件驱动的模拟不包括噪声,因为该实验仅用于确认NSI的功能。除了更新膜电位外,NSI还保存最后接收到的输入的时间戳(tupdated)。
每个微服务都由一个神经元和所有传入的突触组成,因此突触后的AdEx神经元无法直接访问NSI的电压。相反,每次更新时,NSI参数(V、Vrest、Vm、decay和tupdated)都会发送到连接到AdEx神经元的突触。基于此信息,突触根据需要使用公式(10)异步计算神经元的准确膜电位。
![]()
其中 t 是当前时间,Vm是膜电位,Vrest是静止电位,decay是模拟泄漏的衰减因子,tupdated是参数更新的时间。
在CloudBrain中创建了一个由NSI和sCPG组成的网络,以确认NSI能够在基于事件的架构中更新突触后神经元的电压阈值电位。在这个设置中,sCPG由两个相互抑制的单个神经元组成。图3C显示了CloudBrain中的网络框图。NSI的输入是脉冲信号,因为它是基于事件的架构。输入脉冲相当于基于时间的NEST模拟中使用的步进输入电流。使用Ben's Spiker算法(Schrauwen and Van Campenhout, 2003)将阶跃函数编码为脉冲,以传输到NSI。反过来,NSI根据脉冲输入的频率更新sCPG神经元的Vth (如公式1中所述)。sCPG神经元的Vth是使用膜电位的线性映射计算的。这使我们能够控制Vth的上限和下限。记录NSI的Vm以与sCPG群体的Vth和脉冲输出进行比较。

3. RESULTS
使用148pA的恒定Iinput进行模拟显示NSI膜电位开始接近静止电位-60mV并在-45mV附近结束,尽管这些值因噪声而略有不同。这为我们提供了将NSI的膜电位限制在15mV范围内的最大允许Iinput。
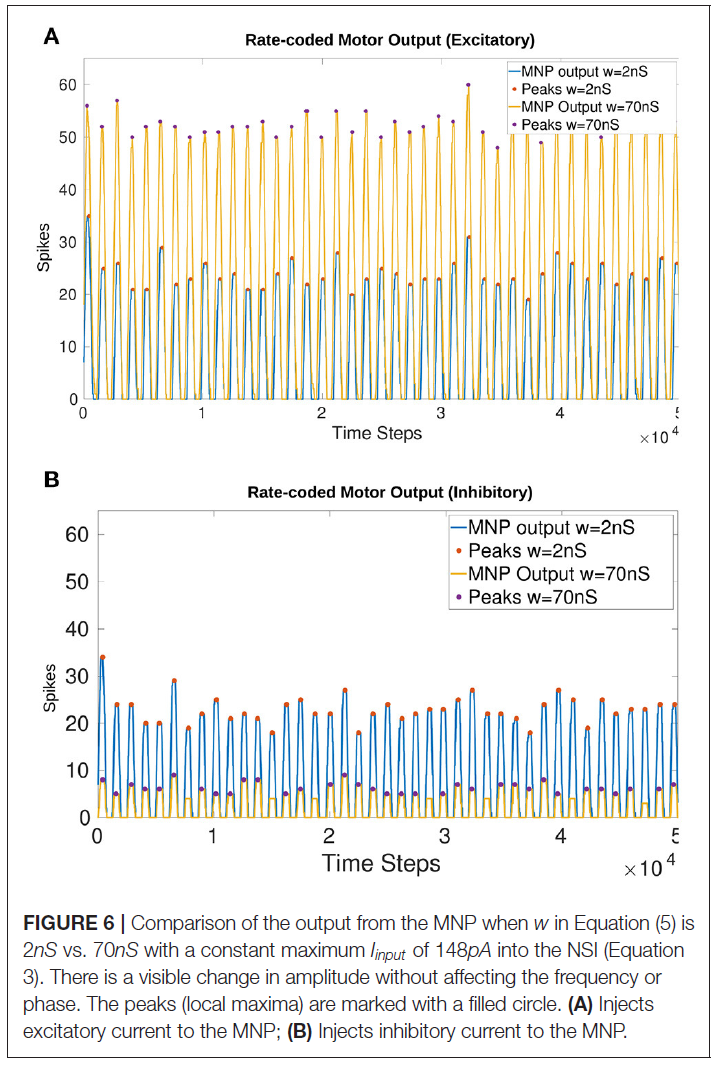
NSI输出突触的最大突触电导权重确定为wmax = 70nS。与2nS的较低权重相比,对幅度的影响在图6中可见。将w增加到80nS会从兴奋性电流注入中产生不需要的提升行为,其中发放率编码输出并不总是返回到零。这个结果可以在补充图1中看到。
图6显示振幅受Iinjection变化的影响,而不会改变兴奋性(图6A)和抑制性(图6B)测试的输出频率或相位。图上的实心圆圈说明了发放率编码输出的峰值(局部最大值)。比较2 vs. 70nS时平均峰值的差异是28.37个兴奋时的脉冲和16.69个抑制时的脉冲。
表3显示了基于MNP注入大小的每5ms时间窗口平均脉冲数的逐渐增加。这表明由于Iinjection导致的输出脉冲数量的变化在一个范围内是可扩展的。
3.1. Online Amplitude Manipulation
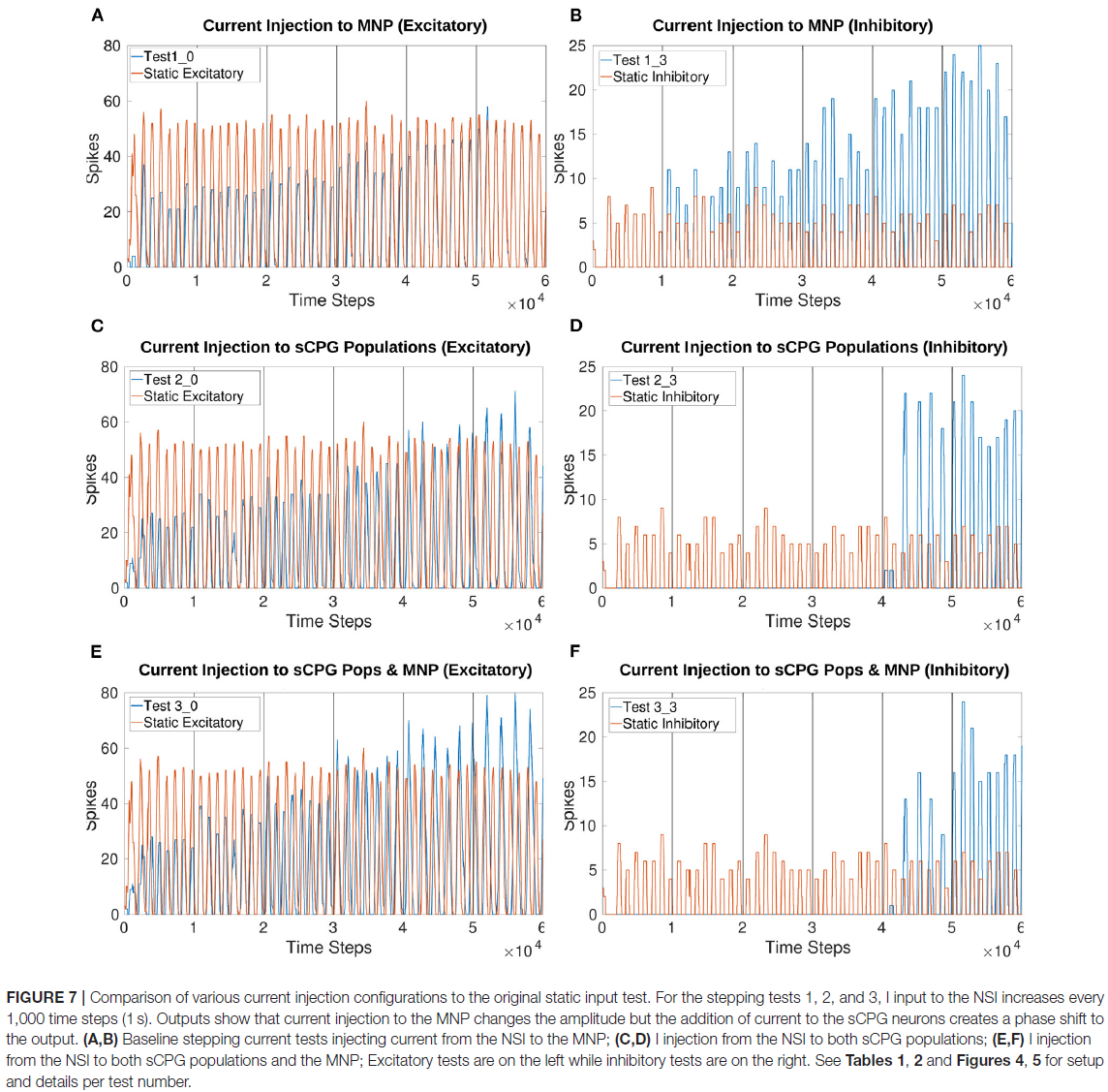
对MNP的Iinjection在线操作导致兴奋性和抑制性测试的每个时间窗口的脉冲数量发生变化(图7A, B)。向两个sCPG群体添加Iinjection会改变脉冲行为,与静态输入电流测试相比,相位发生变化(图7C-F)。此外,两种sCPG神经元群的强烈抑制导致输出的完全抑制。
一次向一个sCPG群体注入电流会导致系统不稳定。补充图4A, B显示,当Iinjection达到特定阈值时,兴奋性sCPG群体的激发会产生提升行为。同样,抑制性神经元群的兴奋增加会抑制MNP脉冲。
补充材料中的所有数字都显示了兴奋性和抑制性试验。在许多测试中,兴奋性电流注入会产生更大的幅度变化,而抑制会抑制输出到某个点。
3.2. Online Frequency Manipulation
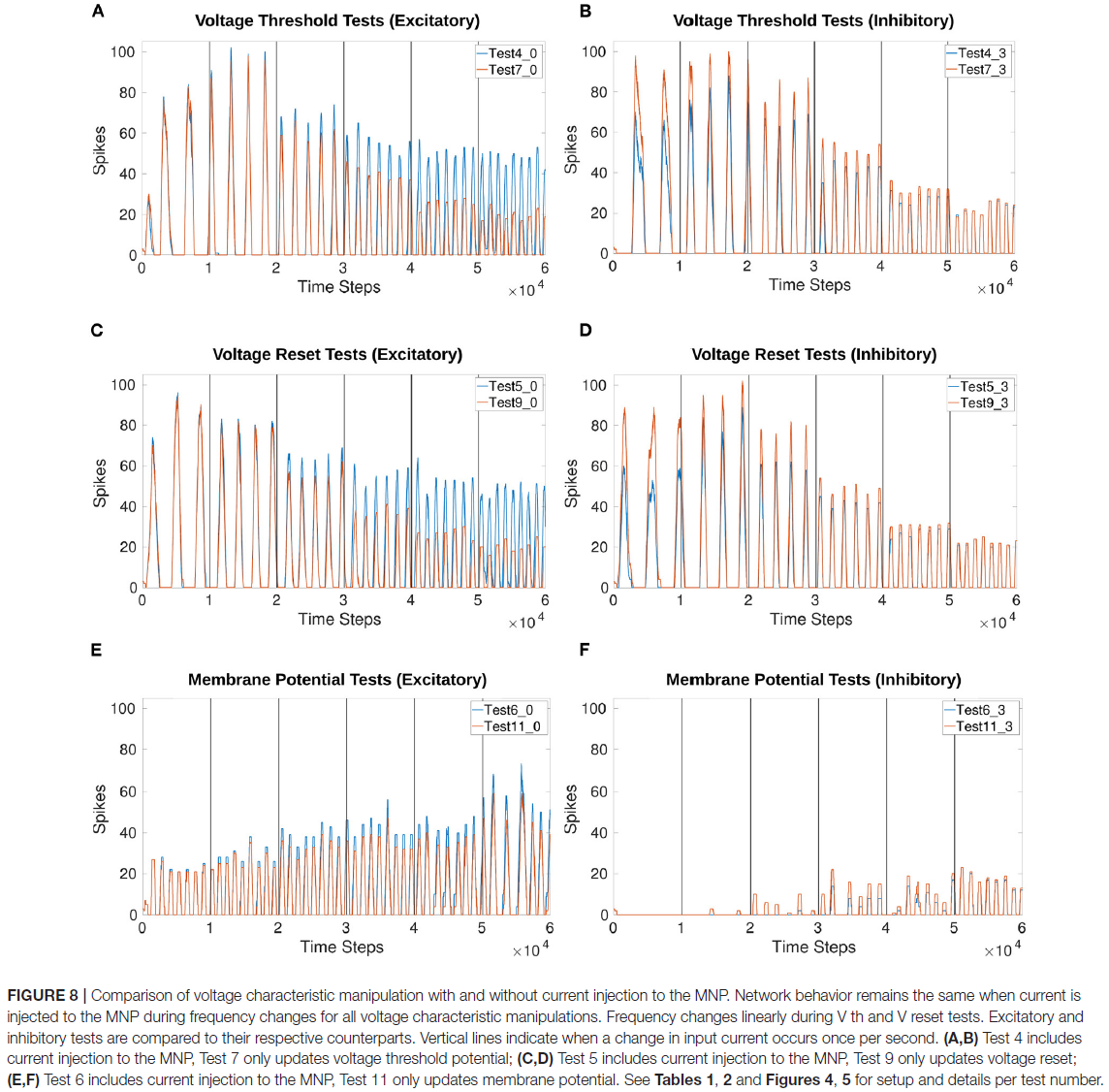
图8比较了在有/没有电流注入MNP的情况下对输出的频率控制。更新sCPG神经元群的Vth或Vreset指向与频率的线性关系。
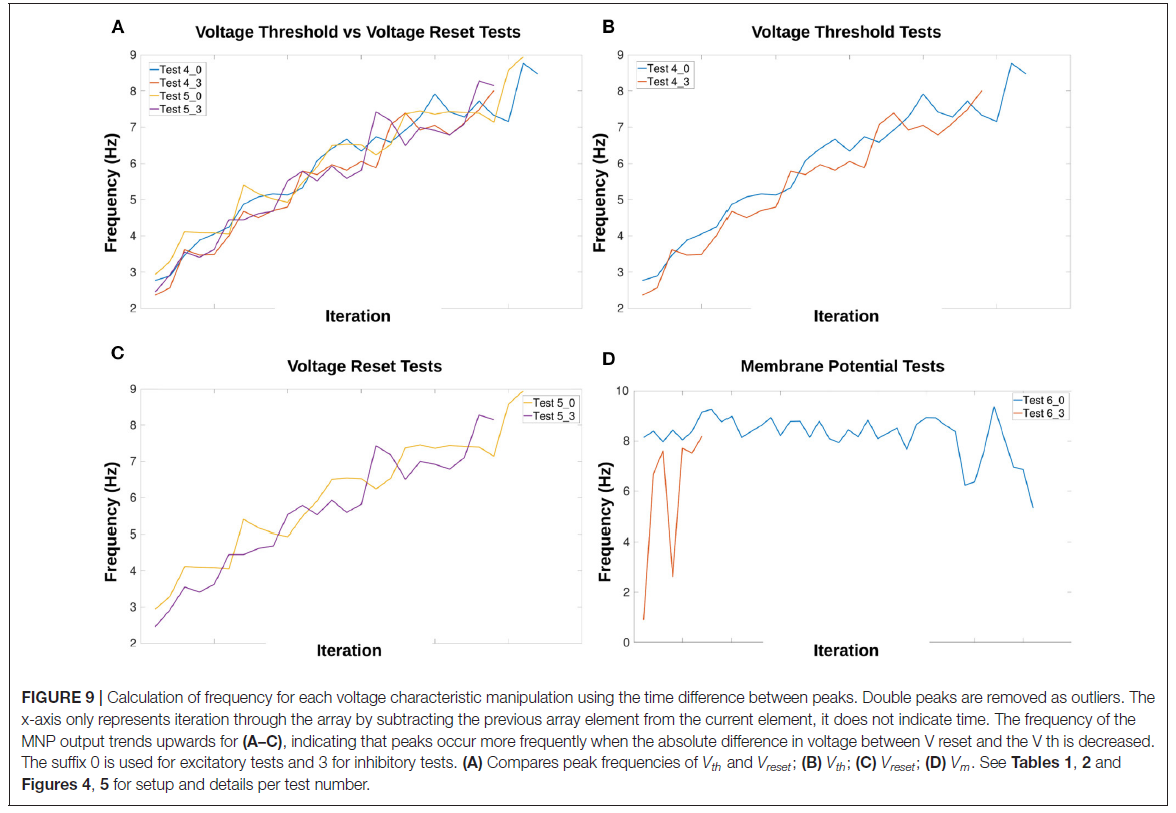
根据电压特性操作计算(公式4),Vth和Vreset在每个时间步骤增加或减少约1。图8A-D显示,通过每秒增加大约1个峰值,它们的操作导致频率增加,这意味着线性关系。图9A-C强化了频率与Vth或Vreset变化之间线性关系的期望。相比之下,向Vm添加偏移并不能可靠地改变频率,并且会随着电流注入的增加而引入不稳定性。图9D显示,对于Vm操作,频率没有倾向特定方向。此外,由于抑制测试的输出在试验的大部分时间里都被抑制,与其他测试相比,数据点更少。
图9A突出显示了比较Vth和Vreset时频率变化的相似性。无论测试是兴奋性的还是抑制性的,这也是正确的。补充表1显示了电压特性操作测试的确切开始和结束频率值。Vth和Vreset测试的起始频率在2.36和2.94Hz之间,结束在8.01和8.94Hz之间。这表明频率可能受3倍的影响。
幅度也受频率影响,每个频率的最大脉冲的平均数量可以在补充表2中看到。频率越低,每个时间窗口计数的脉冲越多,导致发放率编码输出的值越高。这种关系似乎不是线性的,因为与最高的3个频率相比,在比较最低的3个频率时,脉冲的数量减少了更多。
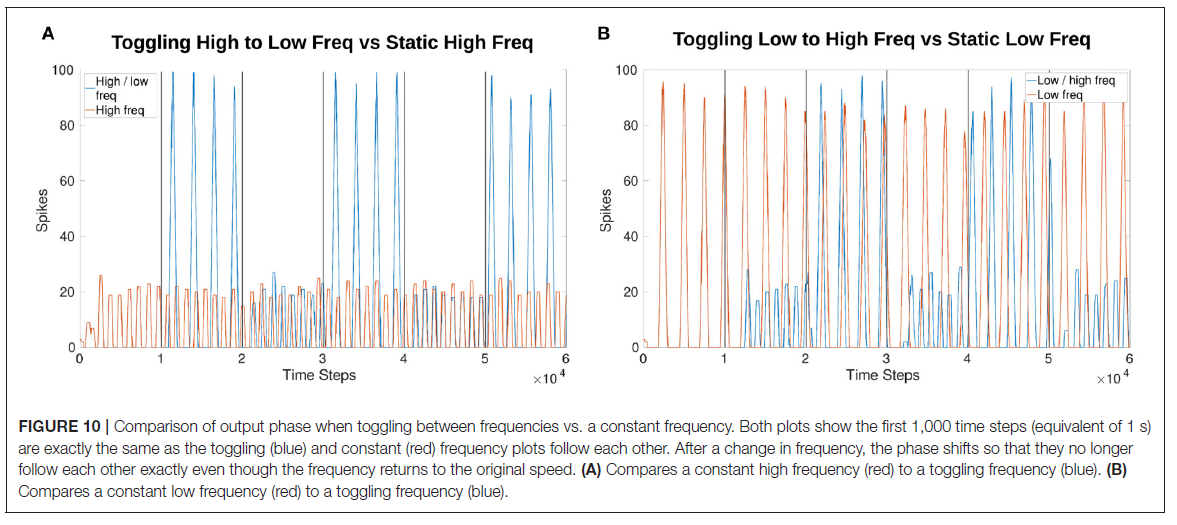
3.3. Online Phase Manipulation
相位受频率操作的影响,如图10所示。图10A, B都显示了仿真的初始1000个时间步骤,产生了完全相同的幅度和相位结果。然而,在频率改变之后相移。
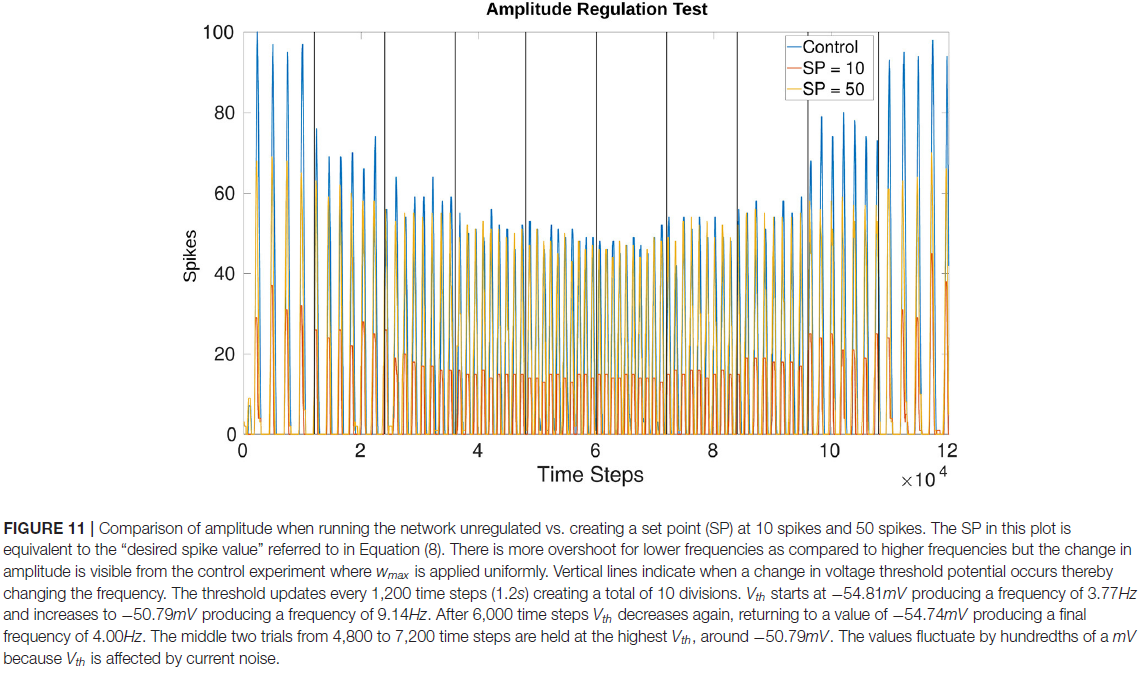
3.4. Online Amplitude Regulation Using Internal Feedback
图11显示了通过调整公式(1)和(2)中的Vth来更新网络频率时的幅度调节效果。Vth根据公式(4)确定的偏移量而变化。发现在没有过度抑制或过度激发的情况下具有最大影响的比例因子:抑制为50,激发为2(插入公式8)。
基于10 vs. 50的"所需脉冲值"(见公式8)的幅度确认网络正在监控输出并进行调整。在比较控制实验(最初测试4_0)和具有所需脉冲值为10的试验时,这一点会更加明显。无论测试是增加还是减少频率,幅度都会调整为类似的值。图11根据所需值和频率确认每个时间窗口的脉冲数量是一致的。此外,相位不受这种幅度调节的影响。
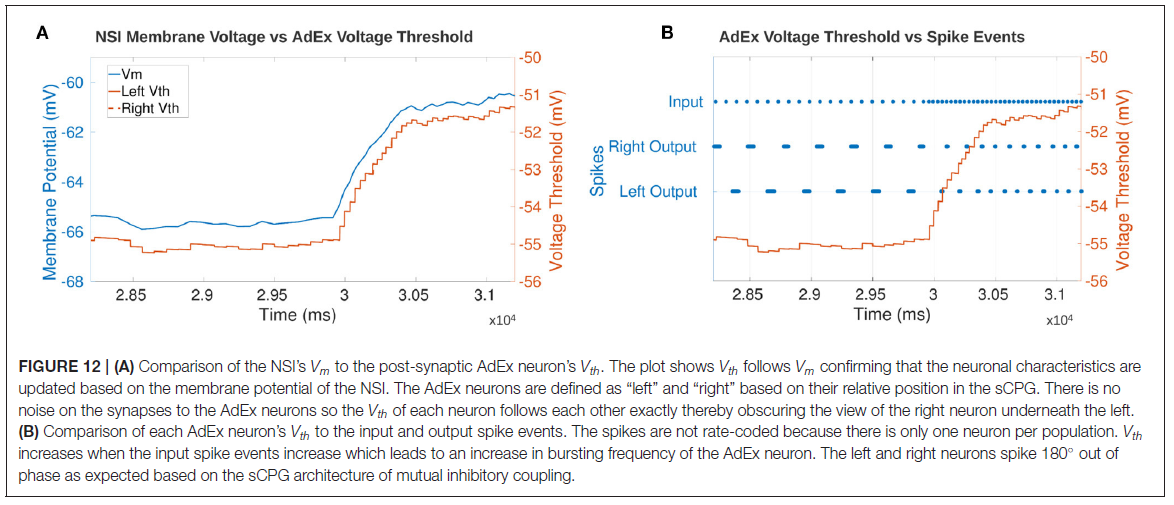
3.5. Event-Driven Manipulation
导致AdEx神经元Vth增加的NSI的阶跃输入如图12A所示。y轴针对每个图形进行了调整,因此不应直接比较曲线的高度。然而,时间轴对于这两个图是相同的,并且显示Vth几乎立即跟随Vm的变化。
图12B确认了当输入脉冲bursting频率增加时AdEx神经元的输出频率增加。该图显示输入bursting频率的增加开始使NSI的Vm上升。这促进了AdEx神经元输出bursting频率的增加。确认AdEx神经元彼此异相脉冲并增加到相同的bursting频率。
4. DISCUSSION
结果证实了我们的NSI模型能够根据不断变化的模拟输入塑造输出并设置sCPG网络的规律模式。NSI对输出的影响量受到限制,因为膜电位的变化必须保持在生物学合理的15mV范围内。然而,该范围仍然允许来自MNP的每个时间窗口的平均输出脉冲至少增加一倍,并且在从低输入电流到高输入电流移动到NSI时将频率增加三倍。MNP的输出还规定了可用的参数范围。使用大于70nS的突触电导时观察到的提升行为意味着由于某些神经元总是发放脉冲,输出不能总是返回到零。这作为输出信号并不理想,因此突触后神经元的最大电导限制为70nS。
基准步进电流测试(1_0和1_3)确认可以通过将注入电流更新到MNP来在不改变系统行为的情况下在线操纵幅度。表3显示可以使用突触电导控制幅度差异。可以从逻辑上得出结论,当没有注入电流时,每个时间窗口的最大脉冲平均数在23到24.26之间。脉冲的数量从这个起点开始增加或减少,这取决于连接是兴奋性还是抑制性。在测试的电流范围内最大脉冲之间的差异是稳定的,加强了电流注入可靠地改变幅度的结论。如果除了当前注入之外突触权重发生变化,则每个时间窗口的平均脉冲数可以从6.31调节到52.63。这种配置将平均脉冲差异增加到8倍 (52.63/6.31 = 8.34)。
将电流注入sCPG神经元群的测试会产生相移。这是意料之中的,因为它们是推动有规律输出的群体。在协调多个关节时,产生的延迟可能是一个可利用的特征。但是,尚未计算出确切的影响,延迟会根据电流注入水平而变化(参见图7)。
在图9中发现的频率和电压阈值电位之间的线性关系与Strohmer et al. (2020)先前的研究一致。因此,复位电位与频率的关系与电压阈值电位相似。这两个特征都会改变神经元膜电位在达到脉冲阈值之前必须改变的量。直接向突触后群体的膜电位添加偏移会引入不连续性,根据偏移值创建小的"跳跃"。在查看图9D时,频率似乎与Vm的变化没有线性相关。然而,这可能是由于本研究中测试的偏移范围有限。
频率与最大脉冲数量的比较取决于为发放率编码选择的时间窗口的大小以及运动群体中的神经元数量。同样,运动群体中的大量神经元会增加最大可能的脉冲。本研究中显示的结果基于5ms的时间窗口和MNP大小(即5)。当将补充表1的开始和结束频率与补充表2中的平均频率进行比较时,静态测试显示更高的开始频率(两个表都位于补充材料中)。静态测试在总共5秒内平均频率,在瞬变情况下删除第一秒。但是,测试4_0每1秒更新一次频率,因此显示的最小频率和最大频率不是平均的而是单次计算。平均过程很可能解释了开始和结束频率的这种差异。这将可靠的频率变化限制为2.8倍的差异。
由于输出信号周期的改变,与恒定频率相比,在一次试验中在低频和高频之间切换会产生预期的相移。这种相移与sCPG网络自身来自MNP的输出有关,并不表示频率变化可能如何影响具有连接振荡器的更大系统。然而,这些结果意味着NSI能够根据生物学研究重置sCPG网络的规律行为(Bidaye et al., 2018)。
一次仅影响单个sCPG神经元群的试验会造成网络不稳定,这很可能是由于网络动态的变化。sCPG群体是相互抑制的,因此一个群体的激发或抑制会影响网络的平衡。这在补充图4中尤为明显,其中兴奋性神经元的过度兴奋导致兴奋性神经元的提升和过度抑制抑制了网络输出。基于这些结果,稳定且可预测的输出需要使用相同的电流注入或电压特性操作来更新两个sCPG神经元群。这个结论只能在相互抑制的sCPG架构中推断出来。此外,该结果无法预测随时间或不同噪声分布的稳定性。
回顾向电机群注入和不注入电流的频率测试表明,幅度根据注入电流的水平进行调整,而不会影响频率。此外,频率同样受到Vth或Vreset变化的影响,但生物学研究表明,电压阈值适应是神经元用来改变发放率的一种策略(Azarfar et al., 2018)。因此,基于研究结果和生物学研究,我们推荐的相互抑制sCPG网络参数操作的方法是向MNP注入电流,同时更新sCPG神经元群的电压阈值电位。
幅度调节是开发具有NSI的闭环自适应控制器的基础。实施的概念验证网络表明NSI能够根据实时反馈控制输出。尽管有证据表明短期可塑性会影响规律输出(McDonnell and Graham, 2017)并且突触权重影响突触后电位的大小(Burrows, 1996),但该方法仅用于演示目的,在生物学上不一定合理。测试网络揭示了所需设定点的明显过冲,但这是意料之中的,因为在抑制启动之前脉冲值必须超过设定点。较低的频率在减少脉冲数量方面也更差,这可能是因为从sCPG群体接收到的显著激发。从控制实验中可以看出,对于最低频率的试验,每个时间窗口的最大脉冲数可以达到100。与在较高MNP输出频率中看到的较低脉冲计数相比,抑制这些高脉冲计数的影响更加困难。
基于事件的CloudBrain仿真的结果与基于时间的NEST仿真一致,表明可以根据NSI的输入来操纵输出频率。这表明NSI可以将脉冲数据和模拟数据转换为网络可用的信息。接收脉冲输入的能力增加了NSI作为一种可能的编码工具的可用性,表明与事件驱动传感器接口的潜力。此外,在基于事件的仿真中实时运行NSI的能力意味着它可以应用于机器人的闭环控制。
5. CONCLUSION
我们研究中引入的方法能够将NSI集成到SNN中以创建混合网络。我们的模型NSI是一个生物学上合理的输入值编码器,接收模拟值作为Iinput并将信息传递给自然输出脉冲的脉冲神经元群。这项研究证实,sCPG网络的幅度、频率和相位可以根据NSI输入的变化进行操纵,这意味着NSI可以作为SNN内的编码机制。此外,网络适应内部信号的能力表明这种设置在自适应控制器中很有用。
我们推荐的将NSI与相互抑制的sCPG网络集成的架构如图4, 布局4,5,6所示,允许通过更改电压阈值电位来调整频率。在这个特定的设置中,网络的平均频率可以在3.0Hz和8.5Hz之间调节。此外,来自NSI的突触电导权重的调节允许每个时间窗口大约6到52个脉冲之间的平均峰值输出幅度。这假设MNP的发放率编码时间窗口为5毫秒,并且在本研究中调查了5个神经元。记录的频率和幅度范围由架构和参数范围决定,因此进一步研究该系统的动态以最大限度地提高灵活性将是有利的。此外,应评估可达到的频率的分辨率,因为这将是自适应控制的重要指标。
应进一步研究NSI的实现,以将现有脉冲神经元模型的亚阈值使用与独特的非脉冲模型进行比较。还需要进一步研究偏移和注入电流方程以及它们各自的参数。此外,可以优化NSI的泄漏常数以确保生物学合理性和有效性。频率和相位以及频率和幅度之间的关系应该被量化,以便可以充分利用这些相关性。振幅可以根据当前注入到MNP的值进行缩放的发现导致使用NSI来确定感官输入的优先级或通知协调任务的可能性。
众所周知,昆虫腿间协调不仅依赖于来自局部腿而且还依赖于相邻腿的感官输入(Bidaye et al., 2018)。因此,可以调整来自单个NSI群体的突触权重,以便向局部腿注入更多电流,同时还向相邻腿提供不同数量的注入电流。
CloudBrain平台上基于事件的演示表明在神经形态硬件上实现是可能的。CloudBrain应进一步研究闭环混合网络,因为它可以与机器人实时通信(Larsen et al., 2021)。这为使用环境交互研究混合网络自适应控制器提供了机会。
亚阈值编码塑造sCPG网络输出的能力为协调和控制任务的新方法开辟了可能性。Storchi et al. (2012)报告观察了生物系统中编码机制组合的使用,表明在单个机器人中使用多种方法可能是自适应控制器的一个富有成效的研究方向。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号