并查集及简单的力扣例题

优秀讲解视频，五分钟让你理解并查集的核心：
youtube.com/watch?v=ayW5B2W9hfo
看完感觉并查集其实也很容易，不是特别艰深的概念

并查集的构成：group，element，father/representative

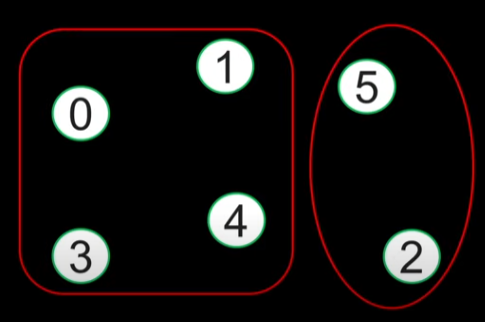
• 并查集的构成就是一系列没有交集的group，每个group里面有很多element

• 每个group有一个representative，将它作为find的返回值和union的依据。
  

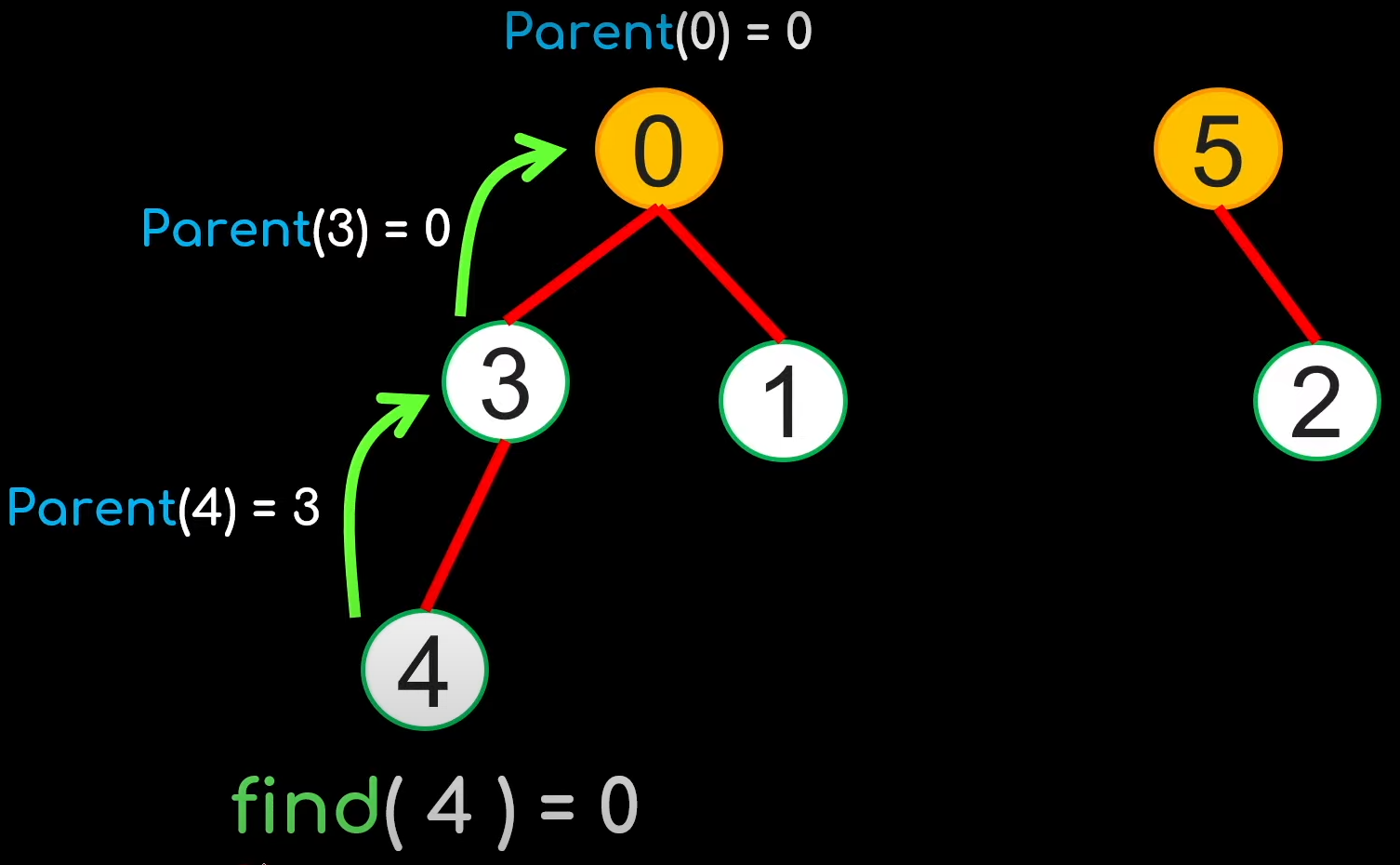
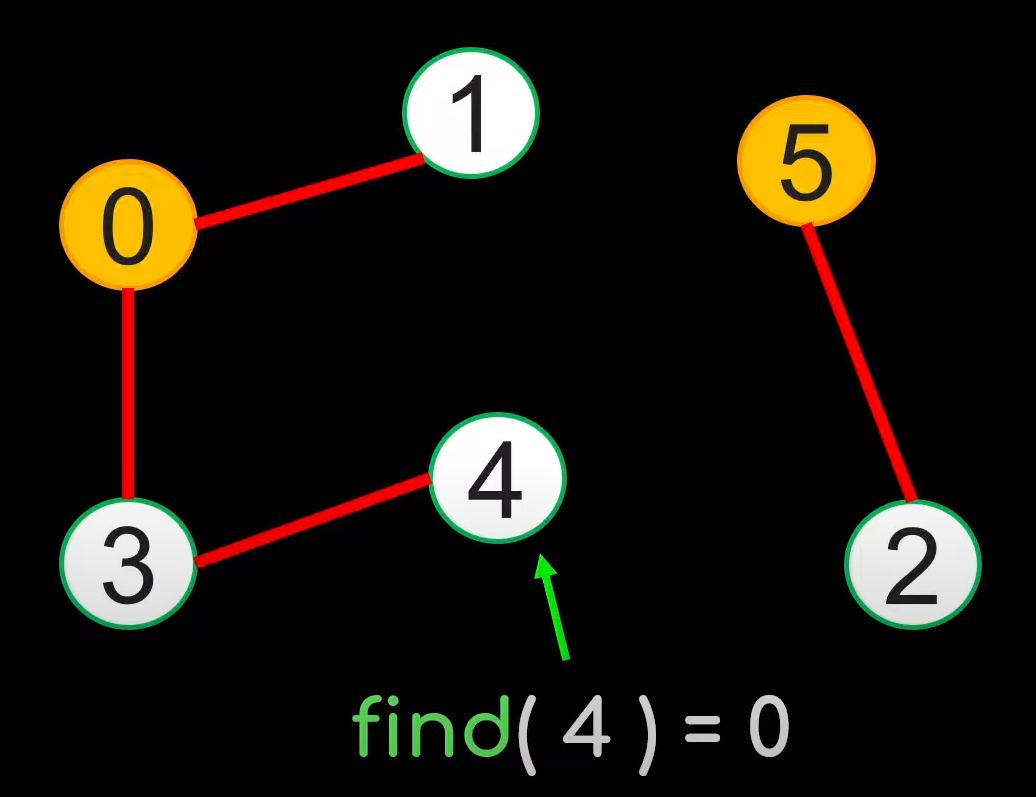
• 组内的element的father都是representative，也是每个element的find结果，比如下图中group[1,0,3,4]的representative就是0。
  

• 这样，可以抽象成representative是树根（father），其他element都是子结点

并查集的两个核心操作

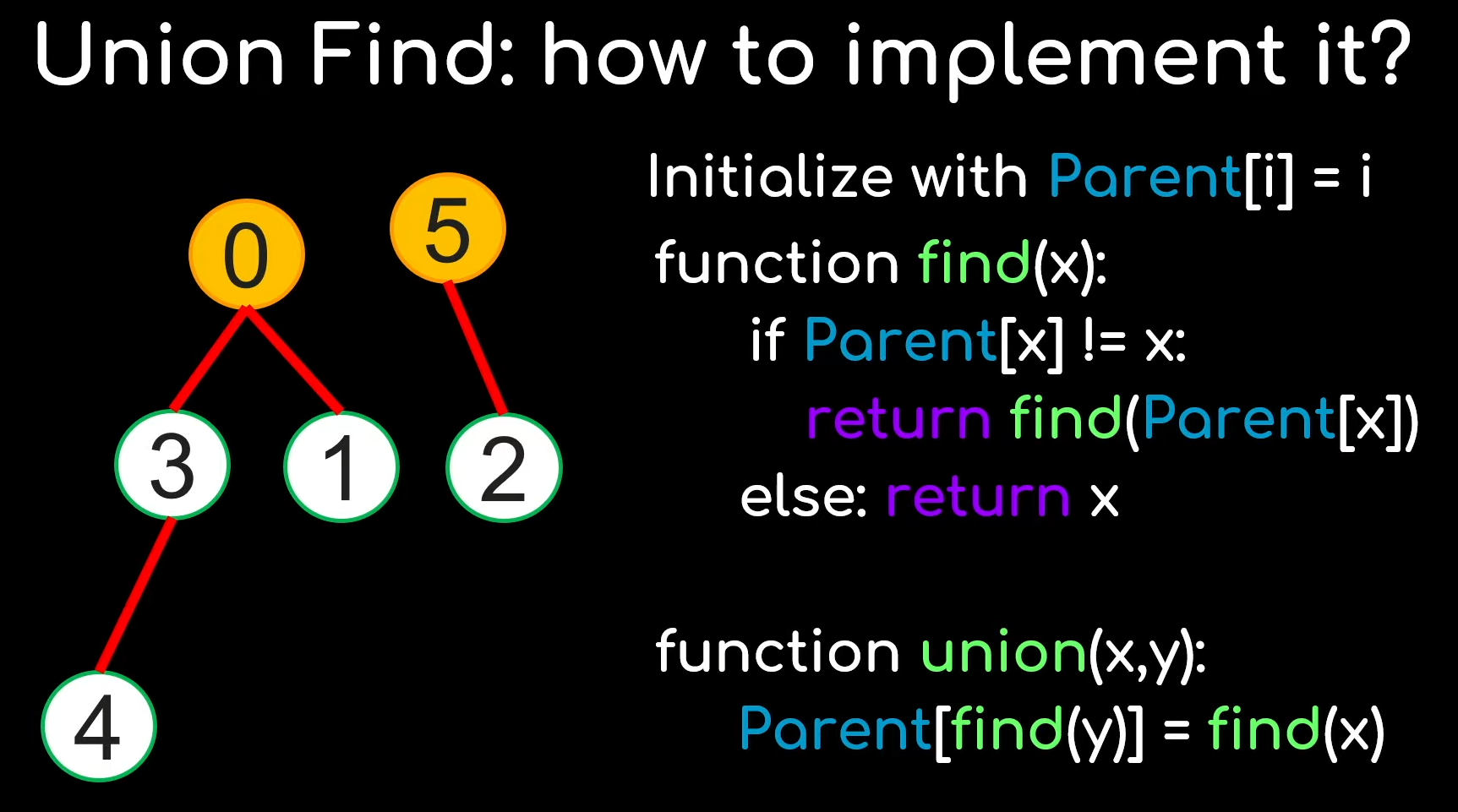
• 并查集操作的核心就是一个union一个find，find用递归实现：

 function Find(x)
     if x.parent = x then
         return x
     else
         x.parent := Find(x.parent)
         return x.parent
     end if
 end function

union直接赋值:

 function Union(x, y)
     xRoot := Find(x)
     yRoot := Find(y)
     if xRoot ≠ yRoot then
         xRoot.parent := yRoot
     end if
 end function

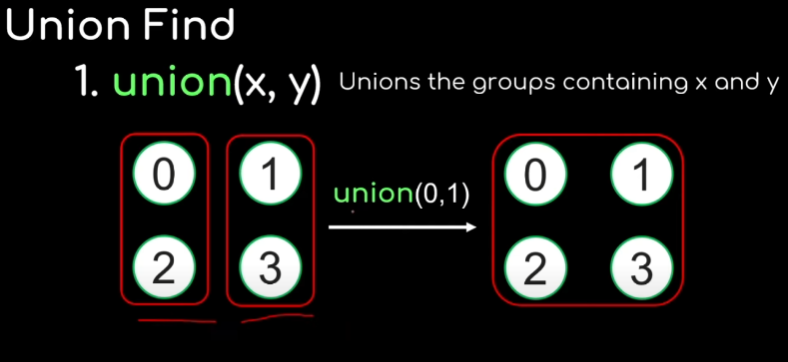
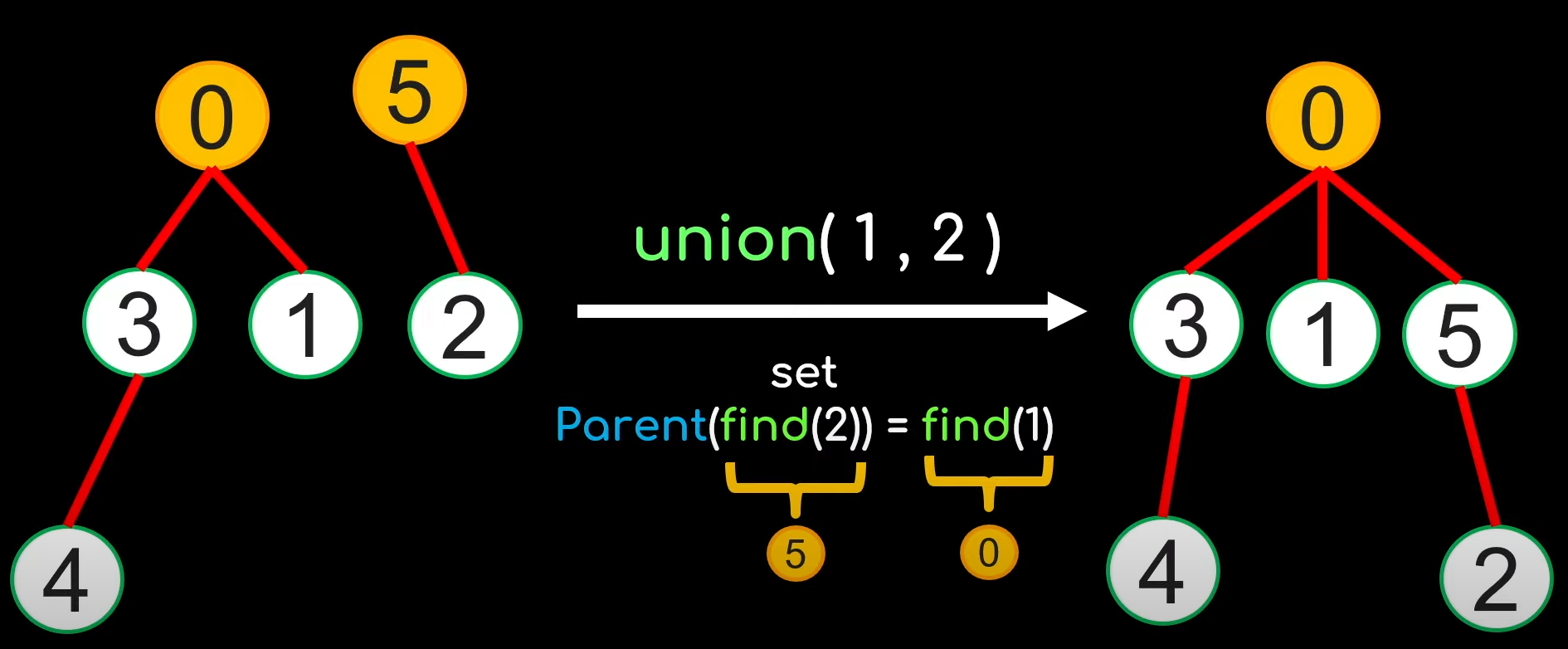
• union把两个group连接起来，其实就是把两个group的father变得一样
  

如何实践union和find？

复杂度分析

假设有n个elements
那平均来说树高的数量级是O(logn)

时间复杂度

find和union都需要反向遍历一个树高，因此时间复杂度是O(logn)

空间复杂度

存储n个element的parent需要用O(n)

力扣例题

684. Redundant Connection
685. Redundant Connection II