CF1973C Cat, Fox and Double Maximum

题目传送门

题面

给你一个长度为$n$的排列，保证$n$为偶数，你需要构造另一个长度为$n$的排列，将两个排列每一位相加得到一个新数列，你要使得这个新数列的极大值最多。

极大值即某个数严格大于他相邻的两个数，位于边界的数字无法成为极大值。

题解

这题是在猜测答案是上界 $\frac n2-1$的前提下完成构造的，做法略巧。

如图，红色部分是给定的排列，我们考虑先把它填平至$n+1$, 即黑线，此时用于填平的蓝色部分也构成一个排列。

我们考虑通过交换蓝色方块，来使得数列满足所有偶数位置严格大于n+1, 所有奇数位置都小于等于$n+1$, 此时达到上界。注意我们不能确定是否存在一种这样的构造方法，但恰巧是有的而且我们想到了，这有很大部分的运气成分。

交换方法是这样的：
因为我们要让所有偶数位置增加，奇数位置减小或者不变，所以每一个偶数位置的蓝色块要换成一个比它更大的蓝色块，我们不妨直接换成比现在蓝色块刚好大1的蓝色块，比如现在有一个蓝色块3在偶数位置，我们考虑将他和4换，若4在奇数位置，则可以直接换，若4在偶数位置，则将4放在3的位置，5放在4的位置， 若5在奇数位置，则将3放在5的位置就好，若5依然为偶数位置，则将6放在5，如此继续直到出现一个在奇数位置的数。

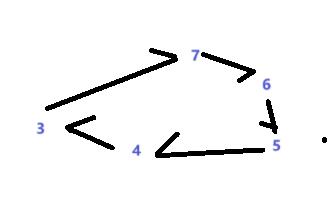
如图，7在奇数位置减小，而其他位置均增大。

问题来了，是否会一直换到$n$都在偶数位置呢？
很简单，若$n$为偶数位，则让所有奇数位为极大值，否则则让所有偶数为极大值，这样就可以保证做法正确。

实现

const int N = 1e6;
int a[N], pos[N];
int ans[N];
int T, ch, n;

int main(){
    T = read();
    while(T--){
        n = read();
        for(int i=1; i<=n; i++) 
            a[i] = read();
        for(int i=1; i<=n; i++){
            pos[n+1-a[i]] = i;
        }

        ch = pos[n]%2;
        ans[pos[n]] = n;

        for(int i=1; i<n; ){
            if(pos[i]%2 == ch) {
                ans[pos[i]] = i;
                i++;
                continue;
            }

            int j = i+1;
            while(pos[j]%2 != ch) j++;
            
            for(int k=i; k<j; k++){
                ans[pos[k]] = k+1;
            }
            ans[pos[j]] = i;

            i = j + 1;
        }

        for(int i=1; i<=n; i++) printf("%d ", ans[i]);
        printf("\n");
    } 
    return 0;
}