骑士共存问题

在一个 n*n个方格的国际象棋棋盘上，马（骑士）可以攻击的棋盘方格如图所示。棋盘上某些方格设置了障碍，骑士不得进入

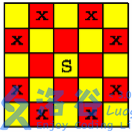
对于给定的 n*n 个方格的国际象棋棋盘和障碍标志，计算棋盘上最多可以放置多少个骑士，使得它们彼此互不攻击

输入格式

第一行有 2 个正整数n 和 m (1<=n<=200, 0<=m<n2)，分别表示棋盘的大小和障碍数。接下来的 m 行给出障碍的位置。每行 2 个正整数，表示障碍的方格坐标。

---

棋盘黑白染色，求最大流即最小割

 

对互相攻击的位置加边，流量为1

注意加边位置合法性

#include<bits/stdc++.h>
#define re return
#define inc(i,l,r) for(int i=l;i<=r;++i)

using namespace std;

template<typename T>inline void rd(T&x)
{
    char c;bool f=0;
    while((c=getchar())<'0'||c>'9')if(c=='-')f=1;
    x=c^48;
    while((c=getchar())>='0'&&c<='9')x=x*10+(c^48);
    if(f)x=-x;
} 

const int maxn=40009;
int n,m,k=1,ans,vis[205][205],s,t,inf=2147483647;
int dx[8]={1,1,2,2,-1,-1,-2,-2},dy[8]={2,-2,1,-1,2,-2,1,-1};

int cur[maxn],hd[maxn],dep[maxn];
struct node{
    int to,nt,flow;
}e[6000005];

inline void add(int x,int y,int z)
{
    e[++k].to=y;e[k].nt=hd[x];hd[x]=k;e[k].flow=z;
    e[++k].to=x;e[k].nt=hd[y];hd[y]=k;e[k].flow=0;
} 

inline bool bfs()
{
    inc(i,1,t)dep[i]=0;
    dep[s]=1;
    queue<int>q;
    q.push(s);
    while(!q.empty())
    {
        int u=q.front();
        q.pop();
        for(int i=hd[u];i;i=e[i].nt)
        {
            int v=e[i].to;
            if(!dep[v]&&e[i].flow)
            {
                dep[v]=dep[u]+1;
                if(v==t)re 1;
                q.push(v);
            }
        }
    }
    re 0;
}

inline int dfs(int x,int flow)
{
    if(x==t)re flow;
    int delta=flow;
    for(int &i=cur[x];i;i=e[i].nt)
    {
        int v=e[i].to;
        if(dep[v]==dep[x]+1&&e[i].flow)
        {
            int d=dfs(v,min(delta,e[i].flow));
            e[i^1].flow+=d;
            e[i].flow-=d;
            delta-=d;
            if(!delta)break;
        }
    }
    re flow-delta;
}

int main()
{
//    freopen("in.txt","r",stdin);
    int x,y;
    rd(n),rd(m);
    s=n*n+1,t=s+1;
    inc(i,1,m)
    {
        rd(x),rd(y);
        vis[x][y]=1;
    } 
    
    inc(i,1,n)inc(j,1,n)
    {
        int v=(i-1)*n+j;
        if(vis[i][j])continue;
        if((i+j)%2)
        {
            add(s,v,1);
            inc(k,0,7)
            {
                int nx=dx[k]+i,ny=dy[k]+j;
                if(nx<1||ny<1||nx>n||ny>n)continue;
                if(vis[nx][ny])continue;
                else add(v,(nx-1)*n+ny,inf);
            }
        }    
        else 
        {
            add(v,t,1);
            inc(k,0,7)
            {
                int nx=dx[k]+i,ny=dy[k]+j;
                if(nx<1||ny<1||nx>n||ny>n)continue;
                if(vis[nx][ny])continue;
                else add((nx-1)*n+ny,v,1);
            }
        }
    }
    
    while(bfs())
    {
        inc(i,1,t)cur[i]=hd[i];
        ans+=dfs(s,inf);
    }
    
    printf("%d",n*n-m-ans);
    re 0;
}