Convex Contour(计算几何)

题目链接：https://vjudge.net/problem/Gym-101173C http://codeforces.com/gym/101173

题意：给出若干三角形正方形和圆形摆成一排，求它们构成的凸型的周长，三角形正方形边长和圆的直径均为单位长度。

Input
第一行一个整数n表示图形的个数，之后一个长度为n的字符串表示每个图形是什么，T表示三角形，S表示正方形，C表示圆(1<=n<=20)
Output
输出构成的凸型的周长

Sample Input

4

TSTC

Sample Output

9.088434417

思路：题意很直接，分类讨论即可，直接找最左边和最右边的正方形或圆形，中间部分比较好算，计算圆形与三角形的距离时需要注意一段小弧的长度

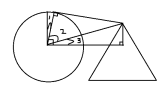
弧长等于圆心角(弧度制) * 半径。

圆心角是∠1，∠1 == pai / 2 - ∠2 - ∠3。

∠2，∠3的三角函数可以求出来。

已知 sinx = a, 则 x = 2π + arcsina。

已知 tanx = b, 则 x = kπ + arctanb。

已知 cosx = c, 则 x = 2kπ + arccosc。

#include<bits/stdc++.h>
#define inf 0x3f3f3f3f
using namespace std;

const int N = 100;
const double pai = 3.14159265;
const double kk = 1.732050807568877;
const double kkk = 0.8660254037844386;

int n;
char s[N];

int main()
{
//    double x = 1 - sqrt(3) / 2;
//    double zz = sqrt(x * x + 0.25) + 6.5;
//    printf("%llf\n", zz);
    scanf("%d", &n);
    scanf("%s", s + 1);
    int pos1 = -1, pos2 = -1;
    for(int i = 1; i <= n; i++)
    {
        if(s[i] != 'T')
        {
            pos1 = i;
            break;
        }
    }
    for(int i = n; i >= 1; i--)
    {
        if(s[i] != 'T')
        {
            pos2 = i;
            break;
        }
    }
    if(pos1 == -1)
    {
        double ans = n + n + 1;
        printf("%.8f\n", ans);
        return 0;
    }
    double ans = n;
    ans += (pos2 - pos1);
    if(pos1 != 1)
    {
        if(s[pos1] == 'S')
        {
            double hi = 1.0 - sqrt(3) / 2.0;
            double wi = pos1 - 1 - 0.5;
            double len = sqrt(hi * hi + wi * wi);
            double now = len + 1 + 0.5;
            ans += now;
        }
        else
        {
            double hi = sqrt(3) / 2.0 - 0.5;
            double wi = pos1 - 1;
            double now = hi * hi + wi * wi;
            double len = sqrt(now - 0.25);
            double tmp = len + 1;

            double val1 = hi / sqrt(now);
            double val2 = len / sqrt(now);
            double ang1 = pai / 2 - asin(val1) - asin(val2);
            double tmp2 = tmp + ang1 * 0.5;

            ans += tmp2;
        }
    }
    else
    {
        if(s[pos1] == 'S') ans += 1.5;
        else
        {
            ans += pai / 2.0;
            ans -= 0.5;
        }
    }
    if(pos2 != n)
    {
        if(s[pos2] == 'S')
        {
            double hi = 1.0 - sqrt(3) / 2.0;
            double wi = n - pos2 - 0.5;
            double len = sqrt(hi * hi + wi * wi);
            double now = len + 1 + 0.5;
            ans += now;
        }
        else
        {
            double hi = sqrt(3) / 2.0 - 0.5;
            double wi = n - pos2;
            double now = hi * hi + wi * wi;
            double len = sqrt(now - 0.25);
            double tmp = len + 1;

            double val1 = hi / sqrt(now);
            double val2 = len / sqrt(now);
            double ang1 = pai / 2 - asin(val1) - asin(val2);
            double tmp2 = tmp + ang1 * 0.5;

            ans += tmp2;
        }
    }
    else
    {
        if(s[pos2] == 'S') ans += 1.5;
        else
        {
            ans += pai / 2.0;
            ans -= 0.5;
        }
    }
    printf("%.8f\n", ans);
    return 0;
}