Luogu8220 solution

Problem

给定起点 \((1,1)\) 和终点 \((n,n)\) 和三元组 \((a,b,c)\)。可以且仅可以在第一象限活动。对于点 \((x,y)\)，如果 \(a\le x\le b\) 且 \(y\le c\)，则经过该点需要单位时间 \(2\)，反之需要单位时间 \(1\)。求从起点到终点的最短路程。

link->https://www.luogu.com.cn/problem/P8220

Solution

从点 \((1,1)\) 至点 \((2,2)\) 有两种方法：

• 直接在 \(x\le n,y\le n\) 的点 \((x,y)\) 上活动。

对于这种方法，又有两种情况。

以样例为例：

1. 先向上再向右：

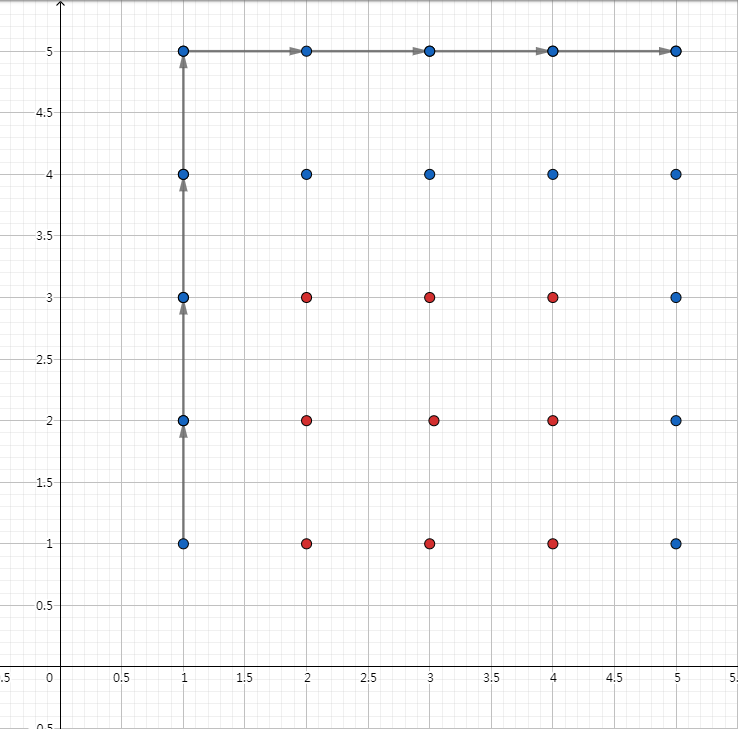
2. 先向右再向上

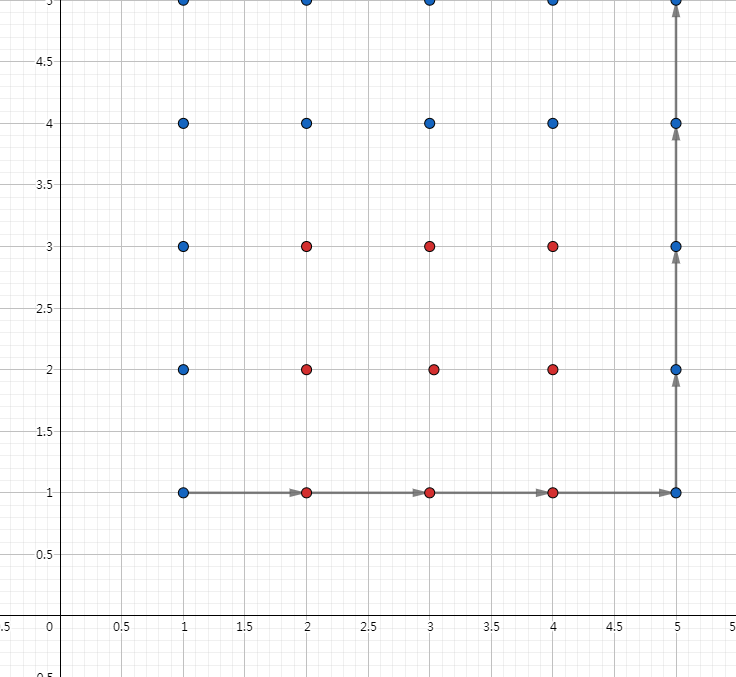
注意到 \(1<a<b<n\)，也就是说起点和终点所在的列一定没有 \(\texttt{B}\) 类点。

右注意到 \(1\le c\)，也就是说起点所在的行一定有 \(\texttt{B}\) 类点。

也就是说，先向上再向右的 \(\texttt{B}\) 类点数量 \(\le\) 先向右再向上的 \(\texttt{B}\) 类点数量。换言之，使用第一种方法一定比使用第二种方法更优秀。

那么怎么计算第一种方法的时间呢？

我们不妨先来考虑没有 \(\texttt{B}\) 类点的情况，接下来再加上路径上 \(\texttt{B}\) 类点的数量，很明显需要 \(2\times n-1\) 单位时间。那么什么情况会使得我们的路径上出现 \(\texttt{B}\) 类点呢？是的，之前提到过，起点所处的列一定不会出现 \(\texttt{B}\) 类点，那么他无疑只会出现在终点所处的行，而出现的情况也显然易见——\(c\ge n\)。而路径（终点所处的列）上，则会出现 \(b-a+1\) 个 \(\texttt{B}\) 类点。

故而，对于这种走法的时间可以一言蔽之：

n*2-1+(c>=n? b-a+1:0)

等等！这就完了吗？不，之前说过有两种方法，接下来让我们看看第二种：

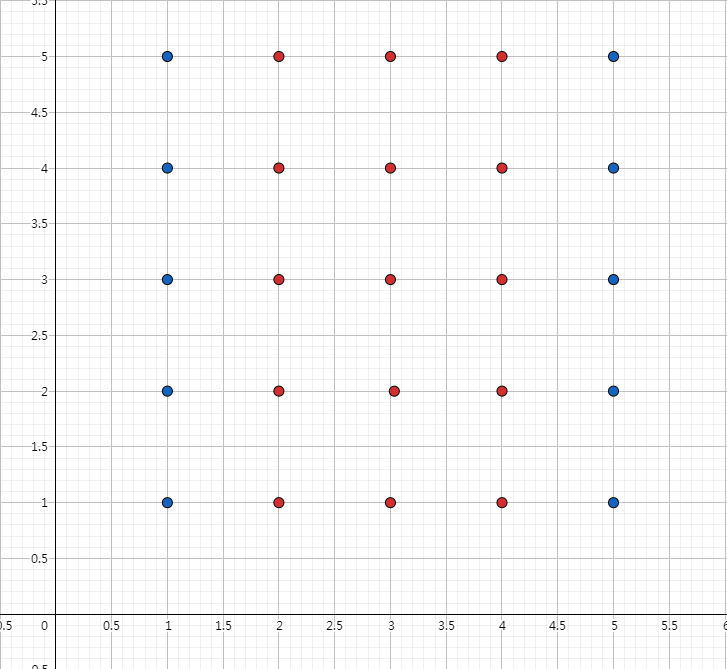
这样怎么办呢？如果使用上述公式我们可以得答案为 \(12\)，但是，这是正确答案吗？别急，先让我们看看另一种方案：

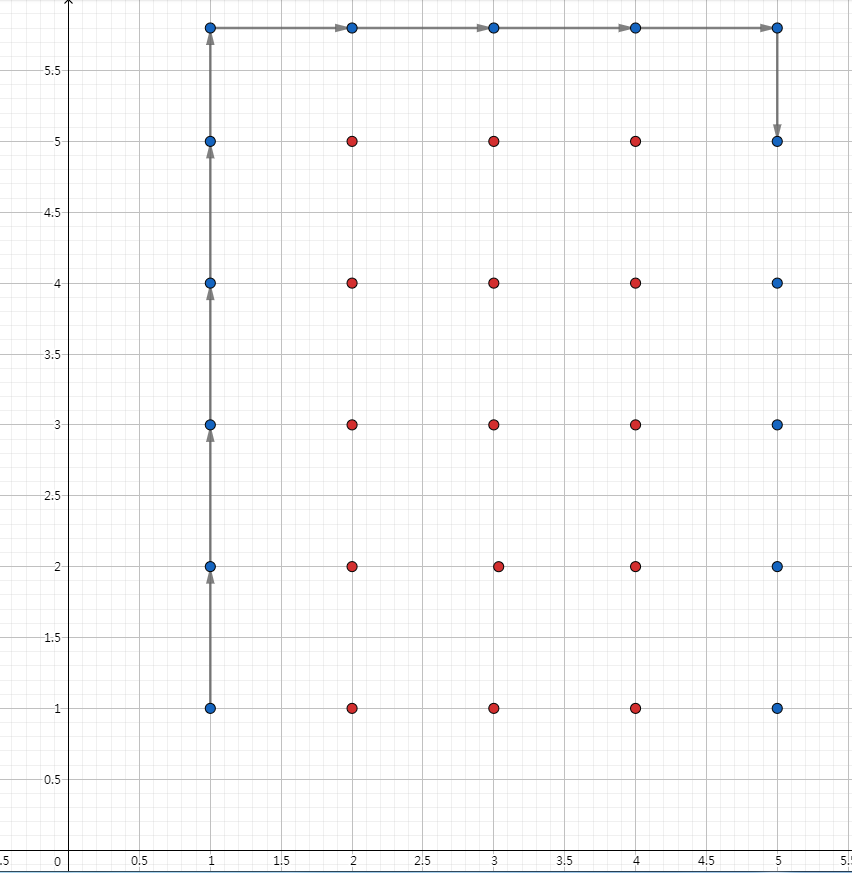
注意了！题目只要求我们要在第一象限活动，而没有要求我们活动的 \(x\) 点 \(y\) 点必须 \(\le n\)。

对于此方案，我们可得答案 \(11\)，较之 \(12\) 更加优秀。

我们可得公式：

c+n+abs(c+1-n)

再对两者取个 \(\min\) 值即可。