Starlink Ku波段下行链路信号结构

Starlink Ku波段下行链路信号结构

来源  https://zhuanlan.zhihu.com/p/638486729

 

StarlinkKu波段下行链路信号结构(翻译)

Signal Structure of the Starlink Ku-Band Downlink

Todd E. Humphreys∗ , Peter A. Iannucci∗ , Zacharias M. Komodromos† , Andrew M. Graff†

∗Department of Aerospace Engineering and Engineering Mechanics, The University of Texas at Austin †Department of Electrical and Computer Engineering, The University of Texas at Austin

原文链接：2210.11578.pdf (arxiv.org)​arxiv.org/pdf/2210.11578.pdf

摘要：我们开发了一种在10.7至12.7GHz频段对Starlink下行链路信号进行盲信号识别的技术，并提供了信号结构的详细图片。重要地本文提供的信号表征包括嵌入在信号中的同步序列的精确值，可以利用这些同步序列来产生伪距测量。对信号的这种理解，对于寻求用于定位，导航和定时的双重用途的Starlink信号至关重要，尽管它们仅用于宽带互联网服务。

关键词Starlink、信号识别、定位、时间同步，低地球轨道

1. 简介
   除了彻底改变全球通信，最近发射的宽带低地球轨道(LEO)巨型星座准备彻底改变全球定位、导航和计时(PNT)。与传统的全球导航卫星系统(GNSS)相比，它们提供更高的功率，更宽的带宽、更快速的多路径去相关，以及更强的身份验证和零年龄星历的可能性，所有这些都将实现更高的准确性和更强的抗干扰和欺骗能力[1]-[5]。
   由于已经有超过3000颗卫星进入轨道，SpaceX的Starlink星座在LEO宽带提供商中享有最成熟的部署。最近使用Starlink信号进行基于机会主义多普勒的定位[6]-[8]的演示开辟了令人兴奋的可能性。但Starlink信号是否更普遍地适用于机会性PNT，不仅通过多普勒定位，以及它们是否可以成为[5]中提出的成熟的GNSS，仍然是一个悬而未决的问题，其答案取决于广播信号的细节，包括调制、定时和频谱特性。轨道、频率、偏振和波束模式的Starlink卫星是由美国联邦通信的许可数据库委员会[9]公开记录的，但它的信号波形本身的详细信息和硬件产生的定时能力不是公开可用的。
   我们提供两个贡献来解决这一知识差距。首先，我们开发了一种10.7至12.7GHz频段的Starlink下行链路信号的盲信号识别技术。该技术是对现有盲正交频分复用(OFDM)信号识别方法的重大扩展(见[10]-[12]和其中的参考文献)，它仅成功应用于模拟的信号。据我们所知，盲识别可操作的OFDM信号，包括精确确定同步序列，以前没有实现过。该技术不仅适用于StarlinkKu波段下行链路，而且通常适用于所有OFDM信号，除了一些估计同步结构所需的步骤可能是Starlink独有的。
   其次，我们详细介绍了Starlink10.7至12.7GHz频段的下行链路信号结构的特征。这适用于当前传输的Starlink卫星(版本0.9、1.0和1.5)，但可能也适用于版本2.0和可能的更高几代，因为需要保留现有用户群的向后兼容性。我们的信号表征包括同步的精确值嵌入在信号中的序列可以是用于生成伪距测量。结合多个伪距测量以实现多点测量PNT是传统GNSS的标准配置，可实现更快和比基于多普勒的更准确的机会主义定位，在[6]–[8]，[13]中介绍了这些定位。并且还可以提供纳秒级精确的定时，而即使在[13]中设想的乐观情景，从基于多普勒的LEO信号中提取时间处理误差在0.1到1毫秒的量级。
2. 信号捕获
   作为介绍信号模型的前奏，我们从详细的开始我们的信号捕获系统描述。
   人们可能会合理地怀疑标准消费者Starlink用户终端(UT)是否可以修改以捕获(数百MHz)宽带信号的原始样本。其实不容易：将UT作为开发硬件，允许捕获原始信号样本，需要破解用于防止这种情况的专门设计。此外，驱动UT下变频和采样的时钟质量未知，并且会因此会污染接收信号的任何时序分析。
   相反，我们选择为Starlink信号捕获开发自己的系统，由现成的硬件和定制软件组成。系统支持从一个Starlink卫星信号一次捕获，再参考高度稳定的GPS振荡器进行下变频和采样。
   消费者StarlinkUT运行由许多独立天线元素组成的相阵，我们的天线是一个可操纵的90cm偏置抛物面碟，波束宽度大约3度。由SpaceX公开提供Starlink轨道星历表指导我们的选择和跟踪卫星。一次只有一两颗Starlink卫星数据波束覆盖[5]。为了保证下行链路活动，我们通过与我们的信号捕获系统位于同一位置的标准StarlinkUT下载高清视频流来请求数据。

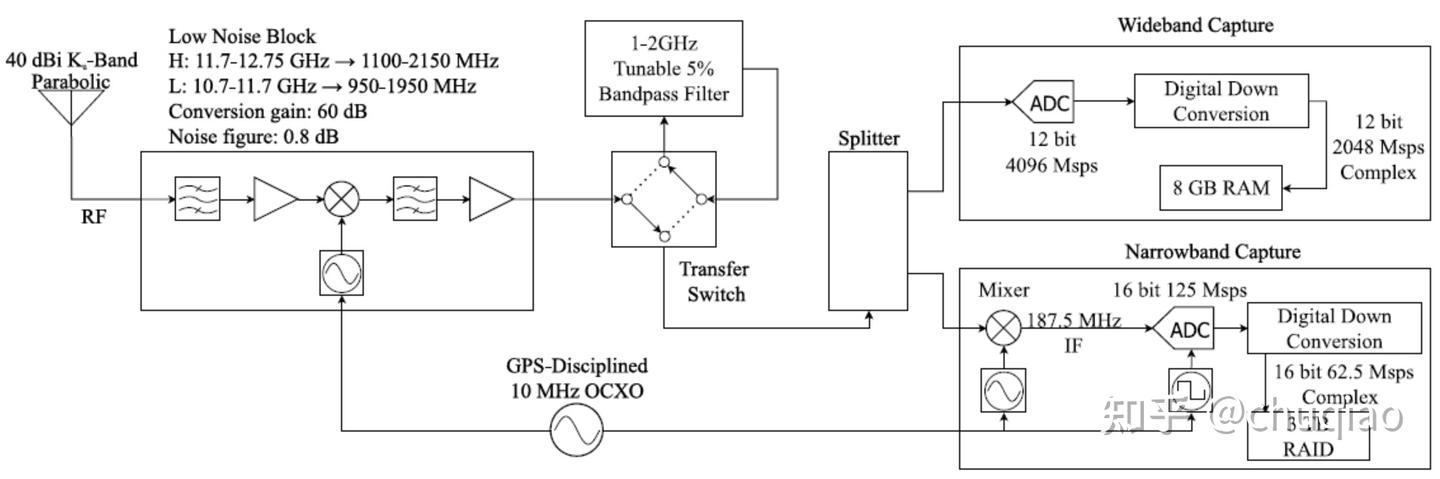
图1Starlink信号捕获流程框图
图1概述了我们的信号捕获硬件和信号途径。抛物线盘将信号聚焦到喇叭上，连接到具有60dB转换增益的低噪声模块(LNB)，噪声系数为0.8dB。LNB是双频的，下变频10.7–11.7GHz(低频段)到950–1950MHz，或11.7–12.75GHz(高频段)至1100–2150MHz。天线的标称增益为40dBi，在12.5GHz，但由于缺乏圆到线性偏振器和馈电喇叭错位，损耗至少为4-5dB。
信号捕获系统允许在窄带(∼60MHz)和宽带(∼1GHz)之间进行选择。对于窄带模式，LNB的输出馈送到转换开关，该转换开关通过可调谐带通滤波器转换信号，用于镜像抑制。然后下游硬件执行下变频(与所选频段一致)，额外的带通滤波和16位62.5Msps的复数采样。LNB中的下变频操作，和下游的下变频和采样操作，使用通用GPS控制的晶体振荡器(OCXO)锁相，以最大限度地减少接收机时钟变化对接收信号的影响。3TB数据存储阵列允许存档数小时的连续数据。
采样前的抗混叠滤波可降低窄带模式的可用带宽至约60兆赫。虽然这比单个Starlink信道窄得多，可组合多个重叠捕获用于全面分析所有窄带结构，如图所示。但是，窄带模式不支持天气信号分析。第二次捕获模式(宽带模式)解决了这一缺陷。基于在4096Msps和12位复采样进行直接数字下变频，宽带模式能够无混叠捕获LNB的整个低频段和大部分高频段。宽带模式的限制是存储、定时、和噪声系数：我们目前的硬件板载存储器只允许1秒的连续数据捕获，采样不是由用于LNB下变频相同的时钟驱动(由于硬件限制)，噪声导致捕获的信号与信号噪声比(SNR)明显差于窄带模式。
对于随后描述的分析，信号识别基于窄带模式捕获的数据，除了估计主同步序列。

1. 信号模型

鉴于其在无线通信中的广泛使用，可以期望OFDM[14]–[18]是Ku频段Starlink下行链路的基础部分。然而，在一直是在卫星通信系统历史上中避免OFDM，因为它的高峰均功率比导致发射功率转换效率低下[19]。尽管如此，检查捕获的Starlink数据生成的功率谱显示，频谱平坦且边缘陡峭，特征与OFDM假设一致。假设OFDM模型后，一般信号识别问题就缩小到识别OFDM信号基本参数值。本节介绍这样的参数，因为它表示通用的OFDM信号模型和接收信号模型。

1. 通用OFDM信号模型
   携带OFDM信号信息的串行数据序列，由从中抽取的复值符号组成集合：

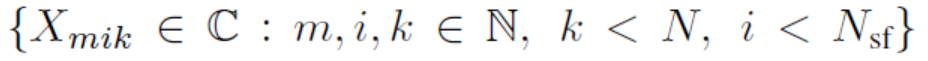
符号率Fs，称为信道带宽。下标k是长度为N的子序列中的符号索引，称为一个OFDM符号，i是OFDM符号，长度-NSF序列的OFDM符号称为帧，m是帧索引。每个符号Xmik编码一个或更多位信息，具体取决于调制方案(例如，1个用于BPSK，2个用于4QAM，4个用于16QAM等)，高阶调制要求更高的SNR以保持给定的可接受的接收低误码率(BER)[18]。OFDM是一种高频谱效率的多载波信号案例，其中每个符号Xmik调制N个具有重叠频谱的相互正交的子载波中的一个。让T =N/Fs是N个信息符号的到达间隔，F =Fs/N =1/T是子载波间距，按指示进行选择，以确保子载波在间隔T内的正交性。然后第m帧的第i个OFDM符号的基带时域信号表示为：

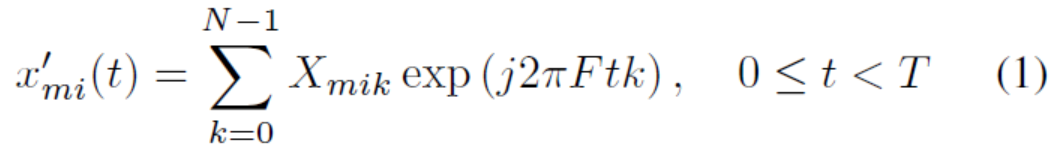
将此表达式表示为离散傅里叶反变换，通常作为IFFT实现。因此可以将每个Xmik视为一个复值频域系数。防止由于多径信道引起的符号间干扰(ISI)，OFDM为每个符号预置循环扩展长度Tg =Ng/Fs的保护间隔，称为循环前缀。由于IFFT的时间循环性质，通过对(1)的简单修改可以对预置操作进行建模：

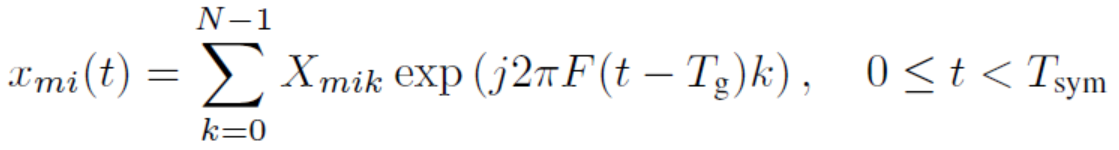
通过添加循环前缀，OFDM符号区间变为Tsym =T+Tg，其中T是有用的(非循环)符号间隔。函数xmi(t)称为OFDM符号，或简称为OFDM符号，如果与其频域表示法几乎没有混淆的风险时。
在所有无线OFDM协议中，OFDM的子序列符号被打包成不同组，称为时隙，帧或块。我们将使用术语帧来描述自包含的OFDM符号的最小分组，从某种意义上说，它包含一个或多个符号可预测的元素，可实现接收机时间和频率同步。设Nsf是OFDM一个帧的符号数量，Tf≥NsfTsym是帧周期，并且

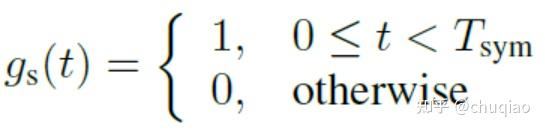
是OFDM符号支持功能。则单帧信号时域可以写为：

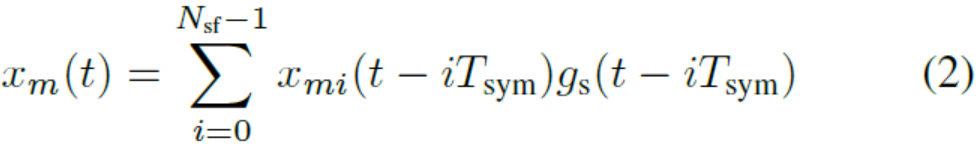
在无限的帧序列上，这变成了

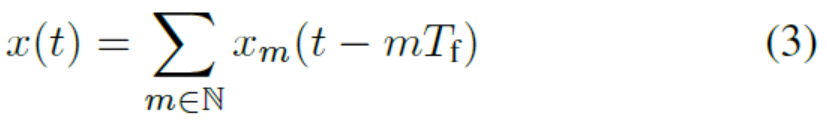
1. 接收信号模型

当x(t)通过LEO-地球信道，稍后通过接收机信号调整和离散化操作时，它会受到多径引起的衰落、噪声、多普勒、延迟、滤波和数字化。

在我们的信号捕获设置中，接收天线高度定向，位于建筑物顶部，视野清晰天空，用于跟踪高程卫星角度大于50度。因此，接收到的信号延迟扩散可以忽略不计——类似于[20]。在这种情况下，相干带宽主要受Ku波段大气色散的限制，如[21]所述，相当于亚毫米级延迟对干燥气压、水蒸气和表面空气敏感200MHz宽信号的温度。鉴于这些优点，我们把LEO-地球信道当作简单的加性高斯白噪模型。

在LEO到地球信道的Ku频段，由卫星和地面接收机之间的多普勒效应相当可观。事实上，多普勒效应非常重要，不能仅被建模为接收信号的频率偏移，如[10]，[11]，或干脆忽略，如[12]。相反，需要一个更全面的多普勒模型，由基带信号的频移和压缩/膨胀组成。

设vlos为卫星和接收机之间速度的大小，假设在一个区间Tf为恒定值，并让β ≜ vlos/c，其中c是自由空间光速。注意在发射器和接收机时钟之间缺乏频率同步，效果与运动产生多普勒相同。在下文中，我们将β视为参数化运动的加性效应和时钟误差诱导的多普勒，我们将β称为载波频率偏移(CFO)参数。

对于OFDM信道带宽Fs，多普勒的压缩/扩张效应仅在以下情况下可忽略不计：βFsTsync≪1，其中Tsync是OFDM的符号间隔时间，同步应保持到在1/Fs的一小部分内。违反此条件导致在OFDM接收机中处理离散傅里叶变换运算时产生ISI，与时域OFDM符号边界未对齐。在标准OFDM信号接收环境中，Tsync可以像Tsym一样短，而对于信号识别续集中描述的过程，Tsync>NsfTsym。

考虑在300公里高度的LEO中的发射器，一个静止的地面接收机，仰角高于50度，采用温度补偿晶体振荡器的时钟。由此产生的β仅限于|β|<2.5×10−5。假设Tsync =1毫秒。然后，为了确保βFsTsync < 0.1，Fs将限制为4MHz，远低于Starlink信道带宽。因此我们的多普勒模型必须包括频移和基带信号的压缩/膨胀。

通过这些初步介绍，我们可以介绍基带模拟接收信号模型为

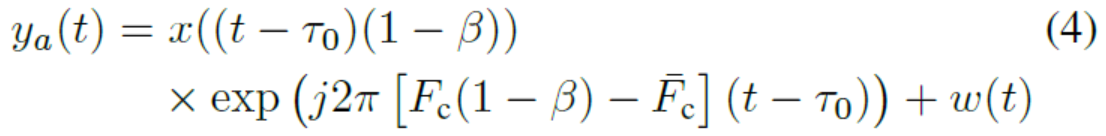
其中Fc是OFDM信道的中心频率，c≈Fc是接收机调谐后的中心频率，τ0是信号从发射器到接收机的路径经历的最短延迟时间，w(t)是复数值零均值白高斯噪声，其同相和每个正交分量具有(双侧)频谱密度N0/2。让符号{Xmik}缩放，使x(t)在非零OFDM符号上具有单位平均功率。然后在此类符号期间和信道带宽Fs内，SNR =1/ N0Fs。

在图1所示的信号捕获流水线的后期阶段，模拟信号ya(t)是离散化的。让Fr成为接收者的采样速率，h(t)是低通的脉冲响应，具有(双侧)3dB带宽Fh < Fr和滚降的预滤波器，使得频率|f|>Fr/2的功率可以忽略不计，允许无混叠复采样。基带数字化接收信号模型为：

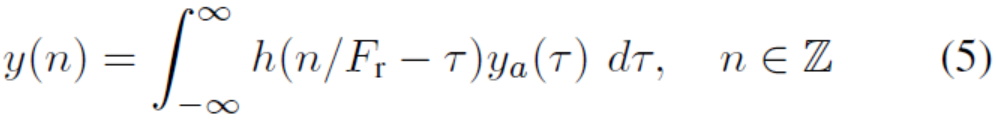
请注意，严格来说，(4)和(5)仅适用于窄带捕获模式。考虑不同的混合宽带模式下的采样时钟需要更精细的模型。

1. 信号初步识别

在这里，我们总结并补充了术语和之前引入的符号，允许清楚地陈述要解决的识别问题。然后，培养关于以下介绍的解决方案过程部分的直觉，我们解释如何利用信号环稳态性以估计关键信号参数。

1. 感兴趣的术语和参数
   我们假设为多频段分配的频谱OFDM信号分为多个OFDM信道，其功率谱密度近似均匀。邻近的信道由保护带隔开。每个信道都是由频谱重叠的N个正交子载波组成。频域OFDM符号是N复值的向量，其中第k个元素调制第k个子载波。
   频域OFDM符号的IFFT，当以保护间隔(循环前缀)为前缀，成为时域OFDM符号。这些符号的子序列是打包到包含一个或多个OFDM符号的帧中携带可预测的元素，称为同步序列，可实现接收机时间和频率同步。传输后，OFDM信号的载波相位在每个帧内保持稳定。帧之间由帧保护间隔分开。可能还有进一步的逻辑子帧结构(例如，时隙、标头段)，但这些在本文的信号识别过程中未涉及。
   请注意，三个不同的结构共享术语“保护”：信道之间的空频谱(保护带)，帧之间的时间(帧保护间隔)和(循环)时域OFDM符号中的前缀(OFDM符号保护)间隔)。
   本文信号的OFDM参数识别问题总结在表1中。
   表1：感兴趣的参数

独立参数
Fs	信道带宽；信息符号率
N	带宽Fs内的子载波数量
Ng	1个OFDM符号保护间隔内的1/Fs间隔数量
Tf	帧周期
Tfg	帧保护间隔
Nsf	一个帧内的非零符号数量
Nsfd	一个帧内的数据(非同步)符号数量
Fci	第i个信道的中心频率
导出参数
T = N/Fs	可用的OFDM符号间隔
Tg = Ng/Fs	符号保护间隔
Tsym = T+Tg	包括保护间隔在内的OFDM符号周期
F = Fs/N	子载波间隔
Fδ = Fci−Fc(i−1)	信道间隔
Fg = Fδ−Fs	信道间的保护带宽度

1. 问题陈述
   本文的盲信号识别问题可以表述如下：给定一个或多个帧长度段由(5)建模的接收数据，估计表1中列出的独立参数值，具有足够的精度，以便在带宽Fh和捕获的时间间隔内确定适用的符号{Xmik}。也识别和评估在一个帧内存在的任何同步序列。
   请注意，此信号识别问题，比在现有盲OFDM信号中处理的那些文献要求更高，有五种方面。第一、无事先识别程序是真正的盲：他们操作研究人员自己产生的模拟信号，独立同分布(IID)信息符号{Xmik}，特性与操作与OFDM信号明显不同。其次，先前的研究要么忽略了多普勒效应或仅模拟多普勒引起的大块频移。第三，先前工作的目标仅限于区分彼此[10]、[12]或来自的已知OFDM波形单载体系统[11]。因此，他们不估计所需的全面独立参数集恢复符号{Xmik}。例如，[10]估计值有用的符号间隔T和符号保护间隔Tg，但不是独立的Fs、N和Ng。第四、现有方法假设接收机带宽Fh宽于Fs，我们的窄带捕获模式并非如此。第五，先前的研究没有关注识别并表征OFDM中的任何同步序列帧。然而，这些序列是标准OFDM信号的关键处理，对于双重目的的努力尤其重要用于PNT的OFDM信号。
2. 利用信号循环平稳性

基于特征的信号识别中的基本概念是信号环平稳性[10]，[22]。虽然所有通信信号表现出周期平稳性，OFDM信号中尤其特别的是循环前缀存在于每个OFDM符号中。

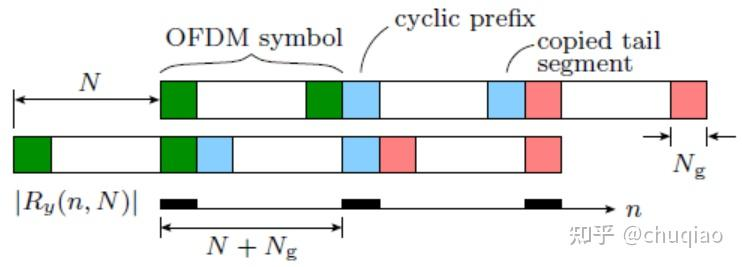
图2图形解释为什么Ry(n,N)在周期为N+Ng的n中是循环的

为了简化本小节中的解释，假设β=0，接收机采样率Fr与OFDM信道带宽Fs相同，并且接收机滤波带宽Fh≈Fs.然后，让E[·]表示均值运算，定义接收的离散时间的自相关函数信号y(n)为

Ry(n, τ) =E[y(n+τ)y∗(n)](6)

其中y∗(n)是y(n)的复共轭。如果系数{Xmik}是iid并从可能的星座值中随机选择，则Ry(n, τ)可能仅在τ∈{0，N，−N}[10]处不为零。如图2所示。非零τ∈{N,−N}处的自相关上升，因为y(n)偏移而产生以循环前缀对齐的方式，对自身与它们符号的副本部分是完美匹配的。图2还清楚地表明Ry(n,N)是循环的在n中，周期为N+Ng。此外，在一个序列中非零OFDM符号，E[y(n)] =E[y(n+N+Ng)]。这些属性意味着y(n)是广义环稳态[18]。自相关函数Ry(n, τ)是确定N和Ng的关键，而无需事先确定时间及频率。由于Ry(n, τ)在n中是周期性的，周期为N+Ng，对于τ的某些值，它可以展开傅里叶级数：

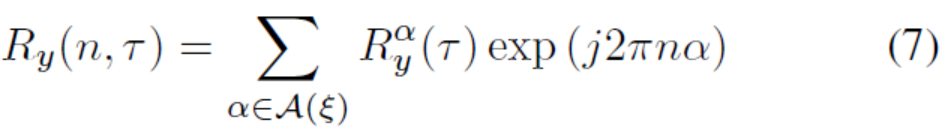
其中A(ξ) ={p/ξ:p∈Z}。特定集合A(N+Ng)包含所谓的循环频率。傅里叶系数Rαy(n, τ)，也称为循环自相关函数，等于

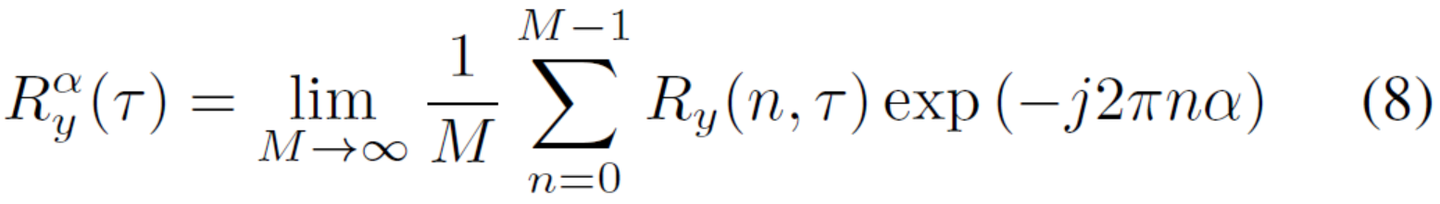
给定Ry(n, τ)的性质，函数Rαy(τ)仅当τ =N且α是来自集合A(N+Ng)的循环频率之一时为非零。这一事实是遵循N和Ng的估计量。设S是可能的集合N的值。然后得到N的估计量为：

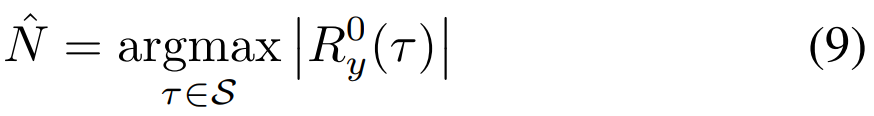
同样，设Sg是N+Ng所有可能值的集合。然后，假设是N的准确估计，则对于Ng估计为：

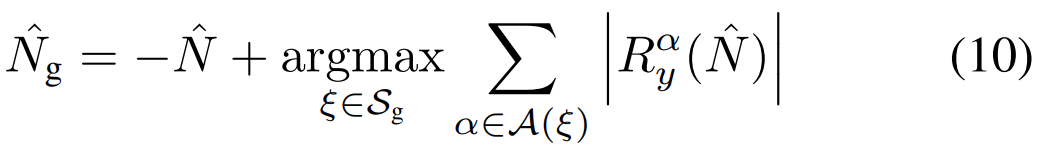
最大化功能的图形描述(9)和(10)在下一小节中提供。请注意，因为这些估计量涉及自相关受限近似偏移|τ|≤N，相当于短时间间隔的T =N/Fs，它们对非零多普勒具有鲁棒性，前提是βFcT≪1。

这两个估计器的数学结构与[10]中提出的基于循环相关的方法相似，除了它们是相继而不是联合运行，这使得它们的计算效率更高而不会损失准确性。

观察到两个估计都基于(8)中给出的循环自相关函数。实际上，此函数近似为：

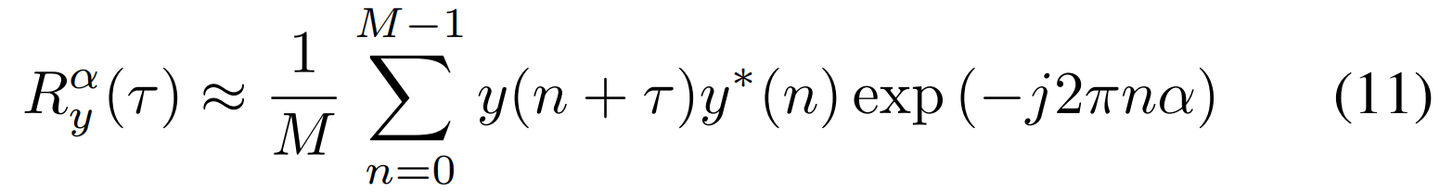
其中M是一个比循环周期N+Ng大得多的数字，例如一帧中的样本数量，甚至多帧(如果涉及帧到帧关联)。

1. 信号识别程序

我们在这里介绍针对第4-B节提出的问题的信号识别解决方案。为了便于理解，我们以分步过程的形式呈现解决方案。

1. N的估计
   我们首先构造S，即N的可能值的集合。在这里，我们利用了OFDM信号的设计者，选择N时必须尊重的约束。以最大化信号的总数据吞吐量，这对于OFDM信号，所有子载波全部被调制：

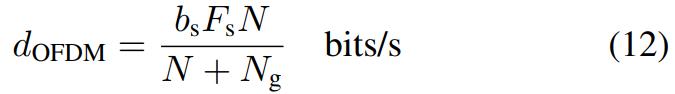
这里，bs是每个符号的位数(例如，2表示4QAM调制)。观察到，对于给定的F和bs，增加dOFDM意味着增加N/Ng。但Ng是信道的物理特性决定的下界：它必须是足够大，以确保Tg = Ng /Fs超过信道的传播延迟。因此，设计者有动力增加N。尽可能最大化吞吐量。但他们必须尊重与子载波间距相关的N的实际上限F =Fs/N：较窄的F对CFO估计提出了更高的要求。设是接收者估计的CFO参数误差β。为避免载波间干扰(ICI)，降低BER，必须满足：
Fc<εF(13)
其中Fc是OFDM信道的中心频率，ε受到限到百分之几[17]。假设已知帧中存在的同步符号允许调制擦除Nsync个连续样本，从相干载波信号可以估计β。在未知相位和幅度进行频率估计问题时，由克拉姆尔-拉奥界给出一个Fc方差的低限[23]：

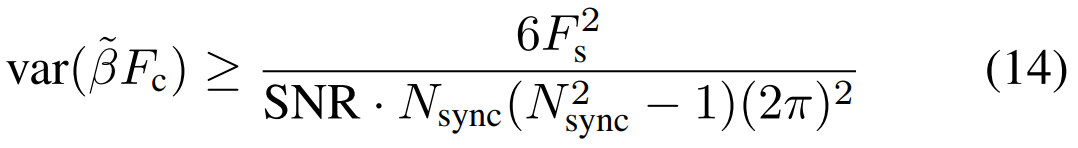
基于此表达式，可以近似地对ε约束如：

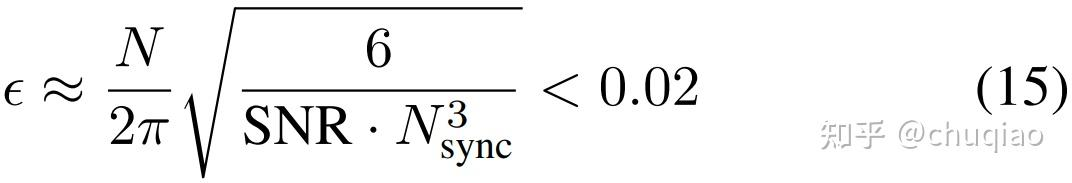
设计人员希望最小化Nsync，因为专用于同步的样本确定性不携带信息。假设Nsync=210，SNR =10dB。那么N必须满足N<5316以确保ε<0.02。
N的另一个实际约束是它必须是2次幂，用于在发射机和接收机上分别高效运行IFFT和FFT。我们知道的OFDM波形没有偏离这一规范。
将2次幂约束与合理约束相结合N满足(15)的值，可以将S构造为
S = {2q：q∈N，9≤q≤12}(16)
(9)假设Fh≈Fr = Fs。但是，当然，在盲识别的背景下操作OFDM信号，接收机的采样率Fr与Fs的关系是先验未知的。准确估计N和Fs的关键是N的2次幂约束。
设是通过检查y(n)的功率谱获得。这可以通过单个宽带捕获，或通过重叠窄带扫描跨越整个信道的捕获。请注意，除了之外，还可以从这次检查中获得信道中心频率Fc的猜测。请记住，即使在高SNR下，不可能从功率谱来精确确定Fs，因为靠近OFDM信道边界的子载波可以保持未调制状态，以提供频率保护间隔[17]。设Nr =⌊NFr/Fs⌉为区间T =N/Fs中有用符号接收机样本的近似数量，其中⌊·⌉表示舍入到最接近的整数。同时设η =Fr/作为估计的采样率比率，并假设|−Fs|/ Fs < p，0<p≪1。然后对于每个b∈S，一组对应的Nr值可以构造以解释中的不确定性：
Srb = {τ∈N：bη(1−p) ≤ τ ≤bη(1+p)}(17)
Nr的完整可能值集是这些值的并集：

换句话说，对于每个b∈S，Sr包含一个Nr的相应可能值的集合，其宽度取决的假设精度。为方便起见，定义fr：Sr→S作为Sr可能值到以S相应值的映射函数;即∀τ∈Srb，fr(τ) =b。
通过这些初步，我们可以重铸(9)中的估计器，对于Fs仅近似已知且可能与Fr有显著差异：

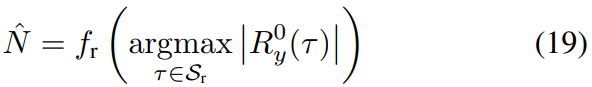
在这里，R0y(τ)由(11)计算。这个估算器用于模拟OFDM信号效果很好，但必须使用应用于操作信号时的验证步骤，由于该如图3所示的现象。顶部面板的蓝色轨迹显示，捕获的Starlink数据的|R0y(τ)|在τ =Nr处表现出清晰的峰值。但峰值的幅度是小于τ∈Sr时的其他合理值，由于实际循环自相关中的突出中心瓣功能。该波瓣是由于自相关滚降较慢造成的，随着|τ|与模拟的OFDM信号相比具有等效的Nr、β、SNR、Fh和Fr(灰色迹线)。这缓慢滚降表示收到的冗余很大信号y(n)在短偏移。这种冗余无疑源于来自(i)强纠错编码的某种组合，(ii)由于微小或可忽略不计数据压缩，以实现低延迟，以及(iii)由导频引起的相邻OFDM符号的相关性。滚降的常规扇形轮廓表明(i)和(iii)可能是最重要的因素。

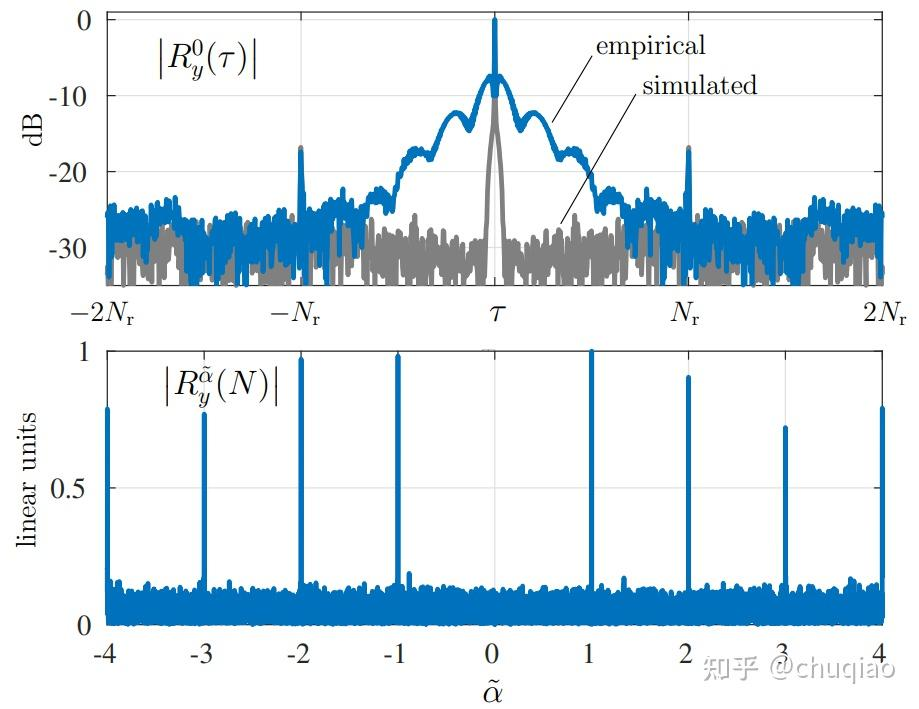
图3 循环自相关函数
上图：α=0时的循环自相关函数为SNR=5.5dB捕获的实际Starlink信号，具有捕获间隔的窄带管道以F̄s宽OFDM信道（蓝色），以及具有IID高斯4QAM符号的模拟OFDM信号（灰色）。模拟信号经过多普勒调整，通过模拟的AWGN信道，在62.5MHz下进行低通滤波和重新采样，以匹配实际信号的多普勒、SNR、带宽和采样率。用于估计Rαy(τ)的样本总数M，通过(11)数量等于Fr=62.5MHz时10ms的样本，结果为跨度刚刚超过7帧。
下图：归一化频率的循环自相关函数， =α(N+Ng)为α∈{p/(N+Ng)：p∈R}，源自相同的实际数据作为顶部面板中的蓝色轨迹，但在Fs=240MHz。基波循环频率处的峰值对应于周期Ng+N出现在=1处;其他峰值出现在该基波的谐波处。
无论如何，为了防止(19)中的最大化，选择一个τ值，在该值处|R0y(τ)|之所以大，只是因为在突出的中心自相关中，被接受仅在以下情况下有效：

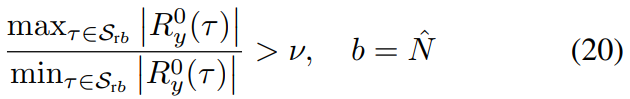
对于某些阈值ν，此测试的重点是确保峰值与邻域其他值足够区分开，即|R0y(τ)|不能有一个宽主瓣，如果此验证步骤失败，则S被重新定义为S←S\，再次应用(19)。根据实际，我们发现对于Starlink Ku波段下行链路信号，阈值ν =10dB足以确保排除杂散最大值。必须选择足够大的p，以确保在验证测试中充分探索非峰值。当Fh明显小于Fr时，这一点尤其重要，在这种情况下，峰值在|R0y(Nr)|可能是几个样点宽。

1. Fs的估计
   获得后，直接获得更准确的Fs的估计。对于b =，定义

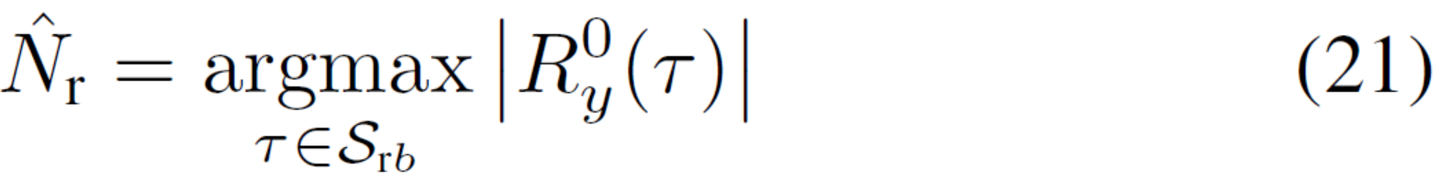
请注意，r/≈Fr/Fs，并且由于大块的带宽由监管机构分配方式的，Fs是极有可能是1MHz的整数倍。因此对于以MHz表示的Fr和Fs，给出Fs的估计器由

该估计器准确性的关键是对的2的幂约束。

1. 重采样
   剩余OFDM参数的估计通过在s处重采样y(n)来执行。回忆(5)，y(n)经过带宽Fh的低通滤波后在Fr处本地采样。对于窄带捕获模式，在s处重采样意味着采样率增加，可以建模为[18]：

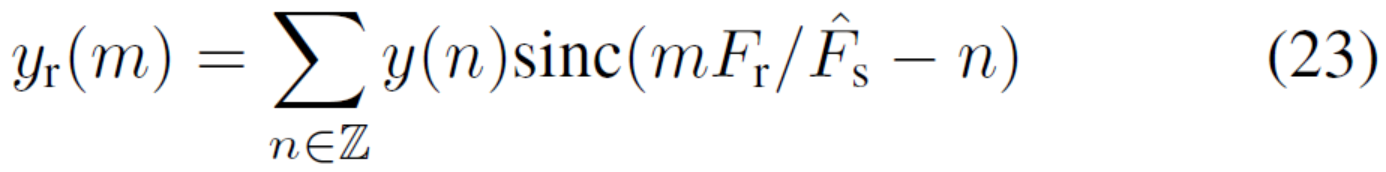
其中sinc(x) =sin(πx)/(πx)。注意有用的频率信号内容，|f|<Fh保持不变。对于宽带捕获模式，在s处重采样意味着转换使用新的低通滤波后，降低采样率较低的Fh。为了符号简单起见，在下文中，我们将从yr中删除下标。因此，y(n)在下文中将表示带宽为Fh的接收信号(可能小于原始)和采样率s。

1. Ng的估计
   从构造N+Ng的可能值集合Sg开始Ng的估计。与S一样，这是由设计约束决定的。从(12)可以清楚地看出，信号设计者希望最小化Ng，但这受约束Tg = Ng /Fs超过最极端的操作条件时信道的延迟扩展。Ku波段最坏情况的95%均方根延迟扩展在[20]为Td =108ns。保守考虑该值的一半到两倍的范围，并假设为了易于实现，Ng是偶数，可以将Sg构造为：
   Sg ={2q+b：b∈S，q∈N，TdˆFs/4≤q≤TdˆFs}(24)
   在s处采样y(n)后，Ng的估计处理在(10)中描述，除了Rαy()由(11)计算，A(ξ)为简化为有限集合A(ξ) ={p/ξ：p∈Z，|p|≤Np}，对一些有限的Np。
   在[10]中分析了该估计量作为Np函数的准确性，表明Np的值高于N/Ng时，没有获得改进。在实践中，当应用于通过窄带模式捕获的Starlink信号，估计器对于低至1的Np，性能是可靠的，前提是(11)中的样本M数至少覆盖一帧(M≥NfFs)，SNR>3.5dB。
   图3中的下部分。显示|Rαy(N)|根据SNR =5.5dB时的实际Starlink数据归一化，使循环频率为整数。这里循环频率的跨度对应于Np =4。
2. Tf的估计
   每个帧包含一个或多个OFDM符号，这些符号具有可预测的元素，称为同步序列，用于接收机时间和频率同步。当同步时序列与接收帧的相应部分对齐时，循环自相关R0y(τ) 出现峰值。因此，帧周期Tf的估计也是基于 (11)中计算R0y(τ)的那样，但采样点的数量M必须大到足以覆盖多个相邻帧。
   设Nf =TfF是用数字帧周期表示的样本数量，并让Sf是Nf的可能值的集合。通过检查期间的信号频谱稀疏的时间段，可以在最小有效信号间隔轻松获得上限Tm的。这个可能是Tf上的松散上限，因为最小的活动观察到的间隔实际上可能是多个帧。然后可构造一个保守的S，如下所示：

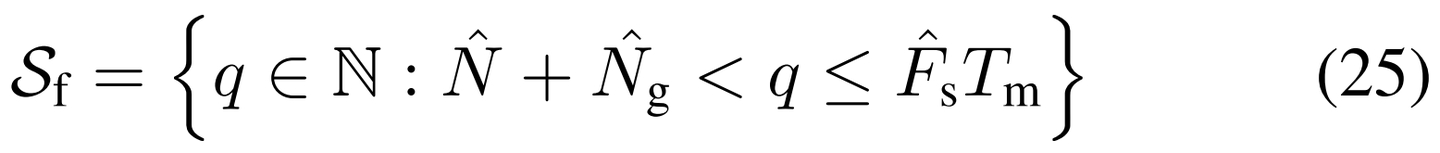
预期信号的考虑因素在估计Tf时再次有用。虽然Tf不需要是毫秒的整数，Nf可能是整数便于信号生成，更重要的是，帧速率Ff=1/Tf几乎可以肯定是整数的赫兹，便于跨星座的帧调度。因此，对于以Hz表示的s，有效估计Tf由下式给出：

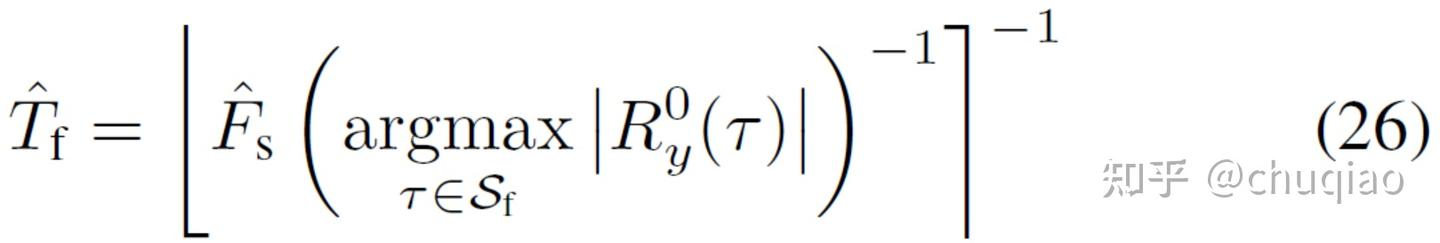
请注意，对于N和Ng的估计量，这个估计量对于Tf对非零多普勒是鲁棒的，前提是βFcTss≪1，其中Tss是任何连续的最长时间间隔同步序列。

1. 符号和载波频率同步
   估计表1中的其余参数和任何同步序列，需要OFDM符号同步和载波频率同步。这种同步必须盲执行，因为设计启用的序列是未知的。
   设nmik是第m帧的第i个OFDM符号的第k个样本，假设i、k、m从零开始索引，对于一些m，i∈N与i<Nsf，我们希望找到nmi0和CFO参数的值β，表示为βmi。
   当帧流量足够低，以至于在帧间存在间隙时，可以观察到在帧开头的样本能量|y(n)|2突然增加，其中允许近似nm00，即第1帧的第1个OFDM符号的第1个样本。通过添加整数倍+g，对所有i∈(0,Nsf)，可以得到近似nmi0。设mi0是nmi0的近似值。然后Smi，nmi0的可能值的集合，可以构造如下：

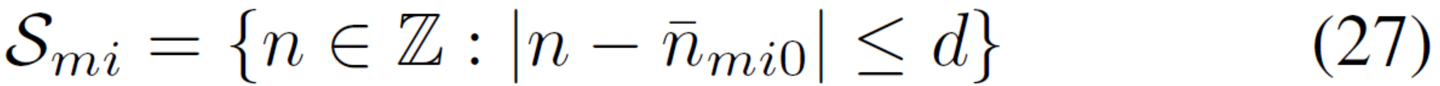
d必须足够大才能解决mi0中的不确定性。
设Bmi是βmi的可能值的集合。可以认为βmi中先验不确定性的范围很小，因为对于已知的接收机位置和时间，并且已知发射卫星星历表，视线速度vlos可以很容易地计算，从中可以计算出β=vlos/c。但回想一下第3-B节，β也代表了用于发射器和接收机振荡器之间的任何频率偏移。在目前情况下，这种偏移的产生可能不只是因为振荡器之间的差异，也因为Fc的不确定性，即捕获产生y(n)的OFDM信道的中心频率。因此，Bmi中包含的βmi值范围，可能是数倍大于仅基于vlos/c的预测值。让mi是基于星历计算和任何其他相关的先验信息的βmi的先验估计值，βm为从mi偏移的最大值，并且Δβ =εs/c是搜索步幅，选择满足(13)，其中c既是先验的通过检查y(n)的功率谱获得的Fc估计，也是捕获以产生y(n)的频段的中心点。那么Bmi可以构造为：

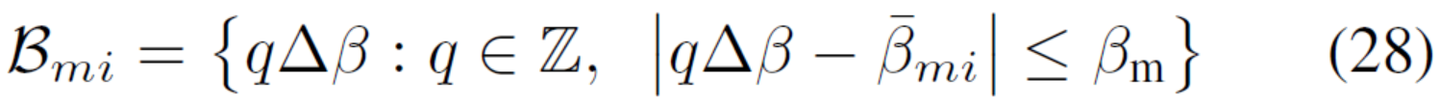
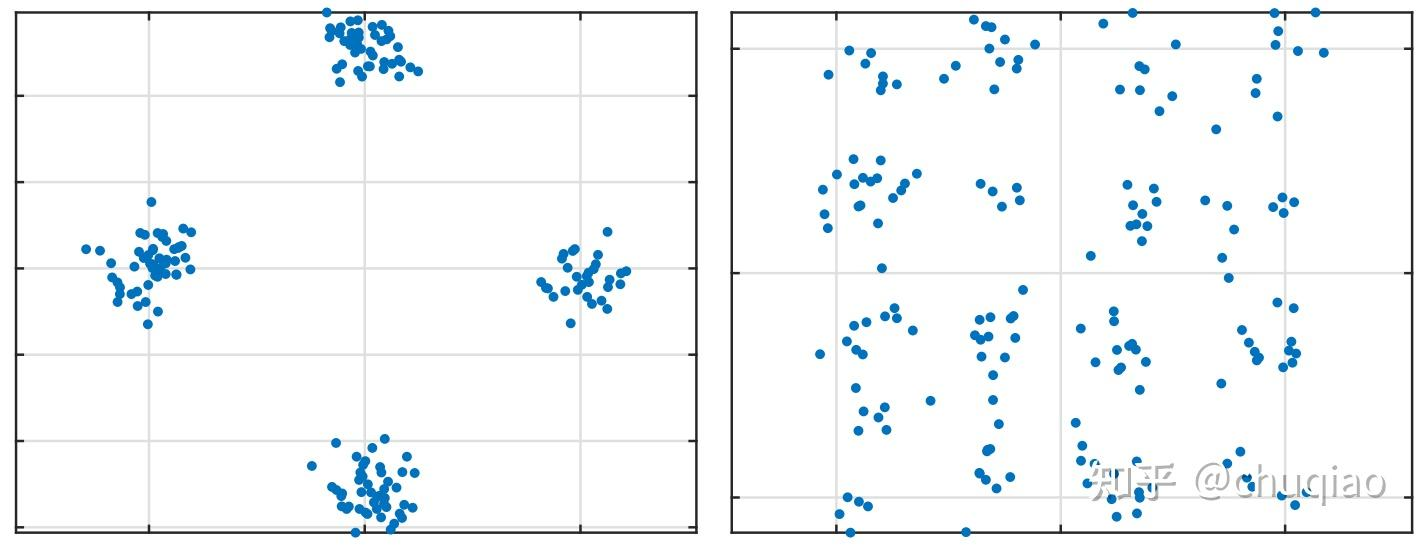
图4： Starlink符号OFDM调制星座图：4QAM (左)和16QAM(右)。
通过同时搜索Smi中的值和Bmi，使用标准接收机处理每个y(n)中的OFDM符号，可以足够准确地估计nmi0和βmi0导致，恢复相关原始信息符号{Xmik}。图4显示了一个频域OFDM符号的部分结果，左边是4QAM调制右边是16QAM调制。左边紧密的星座星团仅在SNR足够高(在这种情况下为15dB)，并且当nmi0和βm的估计值精确到ISI和ICI足以忽略不计时出现。否则簇变细(由于轻微的ISI或ICI)，或他们经历了向原点的完全崩溃(严重的同步丢失)。显然，符号星座可用于开发一个函数，随同步精度而增加。

让SC：Smi×Bmi→R+成为这样一个函数，并试用同步值n∈Smi和β∈Bmi作为参数。算法1显示了SC的计算。首先，以一个试验索引n来分离OFDM符号块。然后对模块进行重新采样并频转以消除非零β的影响，之后丢弃其循环前缀，并把剩余样本通过FFT转换到频域。收到的信息符号结果包含在Y聚类中，如图4所示。假设每个符号有bs位，则出现2bs个簇。这些通过k均值自动识别聚类。对于bs≤2，函数的输出s是实际SNR，计算为每个聚类的质心除以聚类方差的两倍，再取平方幅度的平均值。注意s对星座的旋转不敏感，因为符号{Xmik}的参考相位未知。
使用SC，构造nmi0和βmi0的估计很简单：

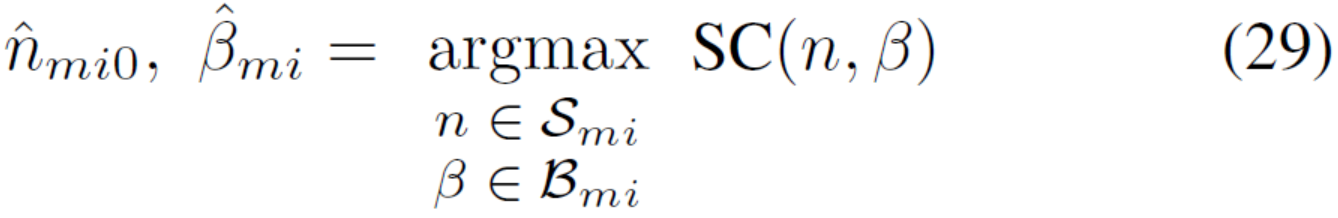
该估计器在捕获的Starlink信号帧的两种类型的的标准OFDM符号调制工作良好，即4QAM(bs=2)和16QAM(bs=4)，即使信号的SNR太低而无法确保无差错的簇识别，如图4右所示。但是估计器在应用于每帧中的第一个OFDM符号间隔。仔细检查显示，此区间不包含OFDM符号而是一个重复的伪随机时域序列。尽管如此，nm00和βm00的估计是准确获得的，为m00 =m10− − g和m0 =m1。

1. 同步序列的估计
   估计嵌在每个Starlink帧中的同步序列是本文的主要贡献之一。对此，必须首先找到序列，即确定帧内的哪个OFDM符号间隔包含可预测的特征。回想一下，根据定义，同步序列从用户终端的角度来看是可预测的。为公共接入OFDM信号，如Wi-Fi、WiMAX、LTE、等等，它们不仅是可预测的，而且从帧到帧都是恒定的帧。假设Starlink信号相同，定位这样的帧内的序列，通过分隔每个OFDM符号间隔，并将其关联到多个帧，以确定候选间隔是否包含帧与帧之间重复的特征。分隔OFDM符号间隔在此阶段是可能的，因为mi0、和g，是可用的。
   该流程显示，在每个Starlink帧的第1个OFDM符号，样本索引nm00开始的帧，包含同步序列。在频域中观察时，发现该间隔缺乏任何可识别的星座结构。但是，它与相邻帧中的第1个符号间隔的互相关揭示了一种峰值模式，表明该间隔由长度为/8 的符号的时域渲染子序列的 8 次重复组成，第一个实例是颠倒的(此同步序列的完整模型将在后面的部分中介绍)。只能使用通过宽带捕获模式获得的数据进行估计，因为子序列的频率内容跨越整个Fs。尽管宽带捕获模式的低SNR，m0，mi0，和g包含的知识允许8个子序列重复连贯地堆叠和汇总，以揭示独特的子序列值，将在下面章节展示。以长度为g的循环前缀前置于8个重复子序列。借用LTE的语言规范，我们将完整的（+g）长序列称为主同步序列（PSS）。结果发现，PSS不仅在同一Starlink卫星所有帧中都相同，在星座的所有卫星上也相同。
   第2个OFDM符号间隔，从样本索引nm10开始，也被发现包含一个（+g）长同步序列，我们称之为辅同步序列(SSS)。与PSS不同，SSS是被发现是标准的OFDM符号，带有4QAM调制。即使使用窄带模式捕获的数据，也能估计信息符号 的，因为落在窄带内的接收符号模式的带宽是可以清楚地观察到的(带一个相位偏移)，如图4左侧所示。
   换句话说，使用高SNR窄带数据，算法1中对应于频率在62.5 MHz窄带窗口，Y中那些元素可以自信地分配给四个簇之一。在这个阶段，不知道是否SSS锚定了绝对初始相位，以便符号在m上是常数，或者经过差分编码，以便只有将是常数，对于k∈[0，N−2]。此外，在这个阶段，各种m上估计m10不够精确，无法确保相应的星座簇可以与从一帧关联到另一帧。因此，最初只有差分值被估计，是的一个估计，其中Ym1k是算法1中Y的第m帧的第i=1个OFDM符号的第k个元素。
   通过连续移动62.5MHz的捕获频段，重复捕获宽度为Fs的OFDM信道，并确保足够的频率重叠，可以自信地估计每个，使得完整的序列可以为2个未知符号确定， Xm12 和Xm1(N/2)。其中第1个从差分估计中无法观察到，因为存在信道中“暗沟”，其中Xmik =0，对k∈{0,1,N−2,N−1}；第2个是不可观察的，因为它位于频带的底部边缘。通过搜索这两个未知符号的所有可能组合，为每个试验组合重新生成一个候选时域OFDM SSS(前面加上适当的循环前缀)，将此候选SSS与已知时域PSS连接起来，并最大化与接收数据帧中的前两个OFDM符号间隔的相关性，同时按照算法1进行重采样，对接收到的数据进行非零β值的频率偏移，可以估计Xm12 和Xm1(N/2)，从而完全确定SSS。与PSS一样，发现SSS在Starlink星座中的所有卫星是相同的。
   每帧的最后一个非零OFDM符号，即一个从样本索引nmi0开始，i =301，发现包含一个（+g）长的同步序列，该我们称之为尾同步序列(CSS)。像SSS，CSS是一个标准的4QAM OFDM符号，其信息符号可由检查确定。CSS符号星座相对于SSS旋转90度：而SSS表现出图4左所示的菱形配置。CSS的星座簇形成一个与水平轴和垂直轴对齐的方盒。
   每帧中倒数第二个非零OFDM符号，即一个从样本索引nmi0开始，i =300，发现以包含一些所有帧一样的常量。但是，与SSS和CSS不同，并非所有信息符号是常数。我们此符号的可预测的元素称之为尾减一同步序列(CM1SS)。
2. 对Nsf、Nsfd和Tfg的估计
   配备mi0 =m10、 、g、f和第一帧中的前两个OFDM符号间隔是同步序列的知识，容易估计Nsf、Nsfd和Tfg。OFDM符号持续时间的估计为sym=(+g) /s，因此，一帧里所有符号数量的估计是⌊f /sym ⌋，其中⌊·⌋表示地板函数。发现最后1个间隔是空的。因此，估计帧中非零符号的数量为：
   sf =⌊f /sym ⌋− 1(30)
   将PSS、SSS、CM1SS和CSS计为同步符号，1帧中非同步符号的估计数是
   sfd =sf − 4(31)
   最后，估计的帧保护间隔，即连续帧之间的空置间隔是：
   fg =f −sfsym(32)
3. Fci的估算

估计Fci，即第i个Starlink OFDM信道的中心频率，由于(4)中β和偏移Fc-c的指数函数，而变得复杂。这意味着先验估计ci中的误差导致与非零β一样的频率偏移。但这两种效果可以通过(4)中的调制x(t)的压迫或扩张完全是β的函数来识别。因此Fci的确定始于对通过x(t)表示的第i个信道估计适用的β，可以通过测量一系列帧到达时间完成。

假设本地接收机用于对接收到的信号进行下变频和采样的时钟是短期稳定且GPS锁相的，与图1中的10MHz OCXO一样。它可以被视为真正的时间参考。设{m00}m∈M是信道i帧开始的样本的索引估计，由(29)或与已知相关的相关性确定PSS和/或SSS。请注意，帧索引集在M中可能没有规则的间距。设定帧m∈M的时间t(m)和接收时间tr(m)为：

t(m) =mf，tr(m) =m00/s

对于长达1秒的间隔，对帧时间的研究表明，这是Starlink卫星上应用时钟校正的节奏，t(m)和tr(m)之间的关系可以精确地建模为二阶多项式：

tr(m) = a0+ a1(t(m)−t(m0))+ a2(t(m)−t(m0))2

其中m0 =最小的M。让是通过最小二乘批量估计获得的系数估计值。则m00 =为帧m0开始时应用的调制估值β。设m00是应用于同一时刻的β值，估计由(29)计算。另外，回想一下，ci是(29)中假设的Fci的先验估计，以及产生y(n)的捕获频带的确切中心值。故有：

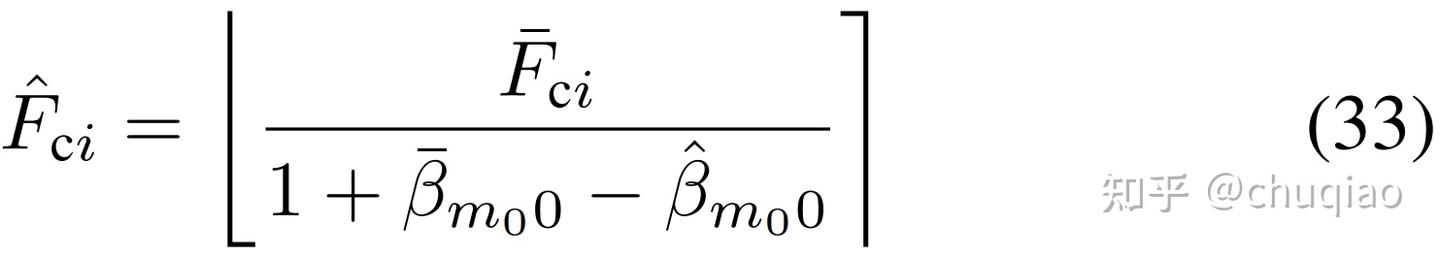
是Fci的估计值，其中ci和ci表示为四舍五入到最接近的MHz，就第(22)项给出的理由是合理的。

1. 结果
   应用前述盲信号识别的过程，产生表2中给出Starlink Ku波段下行链路的参数值。图5和6提供信道和帧布局的图形表示形式。PSS被发现由包含循环前缀的8个N/8长子序列重复构成。如图6，循环前缀和第1个重复子序列实例的极性，相对于PSS的剩余部分是反转的。PSS的时域表达式可以是写成：

 

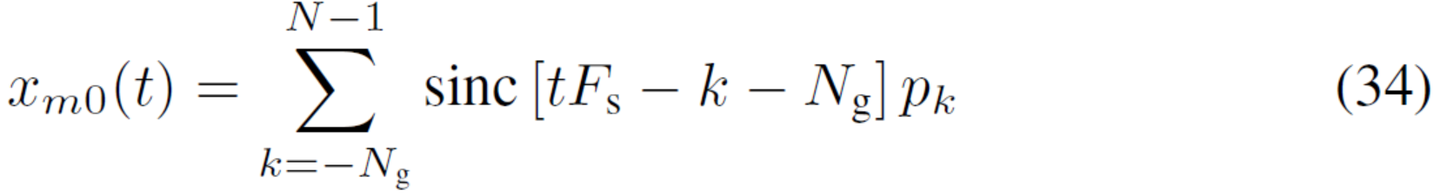
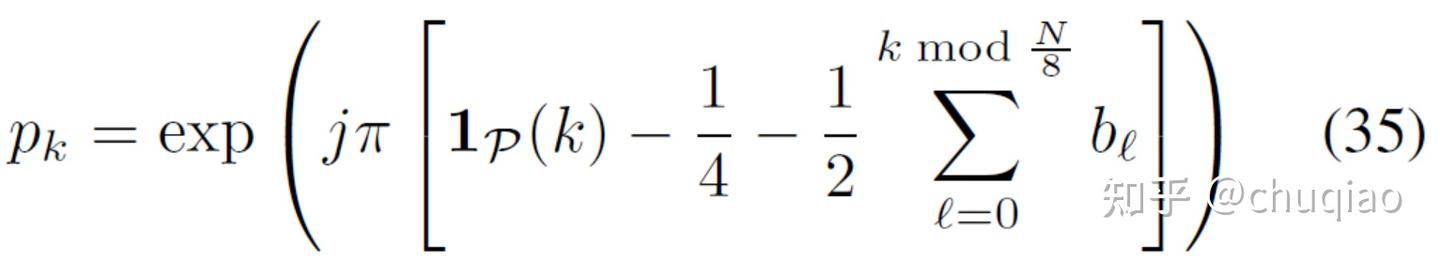
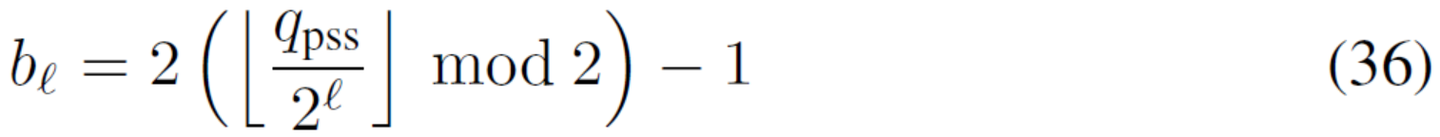
其中1P(k)是指示函数，等于单位k∈P否则为零，P ={k∈Z：k<N/8}。指示函数对k<N/8将相位旋转π，以反转循环前缀和第一次重复的PSS子序列。PSS亚序列(pk)2N/8−1k =N/8是一个长度127的最大长度线性反馈偏移的寄存器(LFSR)序列(m序列)的对称差分相移键控(对称DPSK) 编码。在这种调制中，m序列的每个位表示正或负π/2相位旋转。m序列可以使用7阶斐波那契LFSR，具有原始多项式1+D3+D7和初始状态(a−1,...,a−7) =(0,0,1,1,0,1,0,0)，遵循[24]中的转换。假设LFSR的输出a0,a1,...,a126存储为127位数字，a0存储为MSB和a126作为LSB。将此数字追加0将产生出现在(36)中的128位十六进制数：
qpss =C1B5 D191 024D 3DC3 F8EC 52FA A16F 3958
为了确保正确解释(35)和(36)，我们列出了PSS子序列的前8个值：
pk = exp (jπ[1/4 +qk/2])，k∈{N/8,...,N/8+7}
(qN/8,...,qN/8+7) = (0,1,2,1,0,1,0,1)
SSS的时域表达式可以写为(3)中的xm1(t)，复系数由下式给出：

其中QSSS是十六进制数：
qsss = BD 565D 5064 E9B3 A949 58F2 8624 DED5
6094 6199 F5B4 0F0E 4FB5 EFCB 473B 4C24
B2D1 E0BD 01A6 A04D 5017 DE91 A8EC C0DA
09EB FE57 F9F1 B44C 532F 161C 583A 4249
0A5C 09F2 A117 F9A2 8F9B 2FD5 47A7 4C44
BABB 4BE8 5DA6 A62B 1235 E2AD 084C 0018
0142 A8F7 F357 DEC4 F313 16BC 58FA 4049
09A3 FCA7 F88E 4219 02B6 A258 0AE8 0308
03F6 5809 DB34 7F59 0DBC 46F0 10EB E3A2
5C06 0D74 429F C46B DF9B 6371 9279 798D
232C 5ABA 2741 22FF 66AD 7E44 9F44 CB40
C49C 24A1 E262 9F5B FE82 CE53 1FDC 34F8
C64A 43A9 63F4 0D5B 71BD E6FB 2F13 492D
6F2E 8544 B21D 4497 22C6 3518 0342 CD00
26A1 E7F7 E80E 91B1 75E8 52F9 1976 7E5A
F9B6 E909 AF36 2F52 18E2 B908 DC00 5803
为了确保正确解释(39)，我们提供对应于非零Xm1k的前8个sk值：
(s2,...,s10) = (3,0,0,0,0, 2,1,1)
CSS和CM1SS将在以后的出版物中详细介绍并讨论它们的特征。

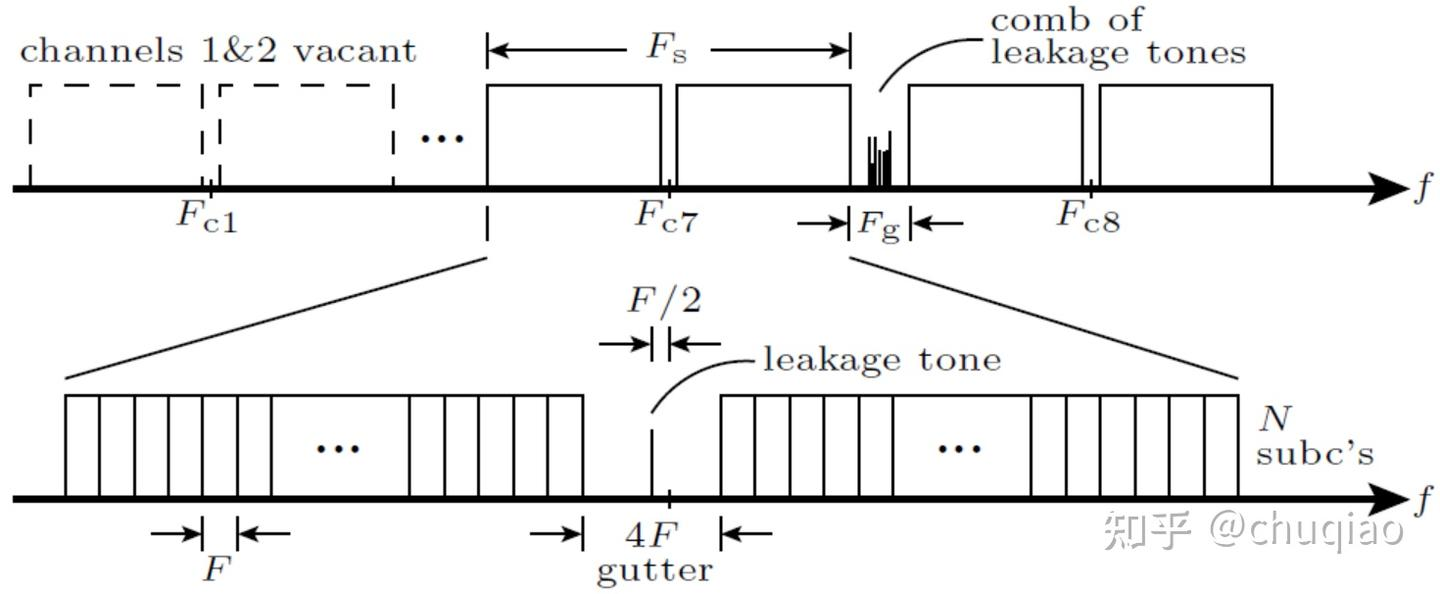
图5：Ku波段Starlink下行链路的信道布局。
表2：Starlink下行链路参数数值

参数	数值	单位
Fs	240	MHz
N	1024
Ng	32
Tf	1/750	s
Tfg	68/15 = 4.533	μs
Nsf	302
Nsfd	298
T	64/15 = 4.266	μs
Tg	2/15 = 0.133	μs
Tsym	4.4	μs
F	234375	Hz
Fci	10.7 + F/2 + 0.25(i − 1/2)	GHz
Fδ	250	MHz
Fg	10	MHz

1. 讨论

我们的盲信号识别过程表明，Starlink Ku波段下行链路信号是简洁的。在LTE和5G NR中，其带宽和双工方案可能因地区而异，其周期性前缀长度可能随时间而变化，Starlink使用了更少的操作模式。本节提供对星链信号显著特征的观测。

1. 频道布局
   如图5所示。Starlink的Ku波段下行链路分配了共8个信道和间隔，每个信道的带宽为Fs =240MHz。一个服务单元内一次只有一个信道处于活动状态。我们假设为了避免小区间的干扰，每个相邻小区都有不同的信道，如[5]中所述，但我们无法通过我们有限的实验验证这一点。较低的两个信道，即以Fc1和Fc2为中心的信道，目前空闲。这可能反映了SpaceX的让步，以避免干扰10.6-10.7GHz无线电天文频段。
   每个频道中央的4个子载波都是空的，留下信道中暗沟。在OFDM实践中保留这样的暗沟很常见，否则，接收机的混频泄漏可能会损坏中央的信息符号。在Starlink的情况，发射器侧一些单音泄漏出现在卫星的暗沟。有趣的是，第i个频道的中心频率Fci，比信道的中点高F/2，它位于中信道暗沟的中心。一个暗沟泄漏单音(如果存在)位于中点。
   带宽Fg =10MHz的保护带分隔了相邻信道。在一些保护带内出现具有时变振幅的梳状泄漏单音。我们怀疑这些是Starlink用于执行基于多普勒的定位的[6]、[7]和[8]。我们注意到，暗沟单音和信道间单音不是故意的：卫星与卫星之间，它们的存在和振幅不是一致的，信道间单音的振幅似乎随波束调整而变化。

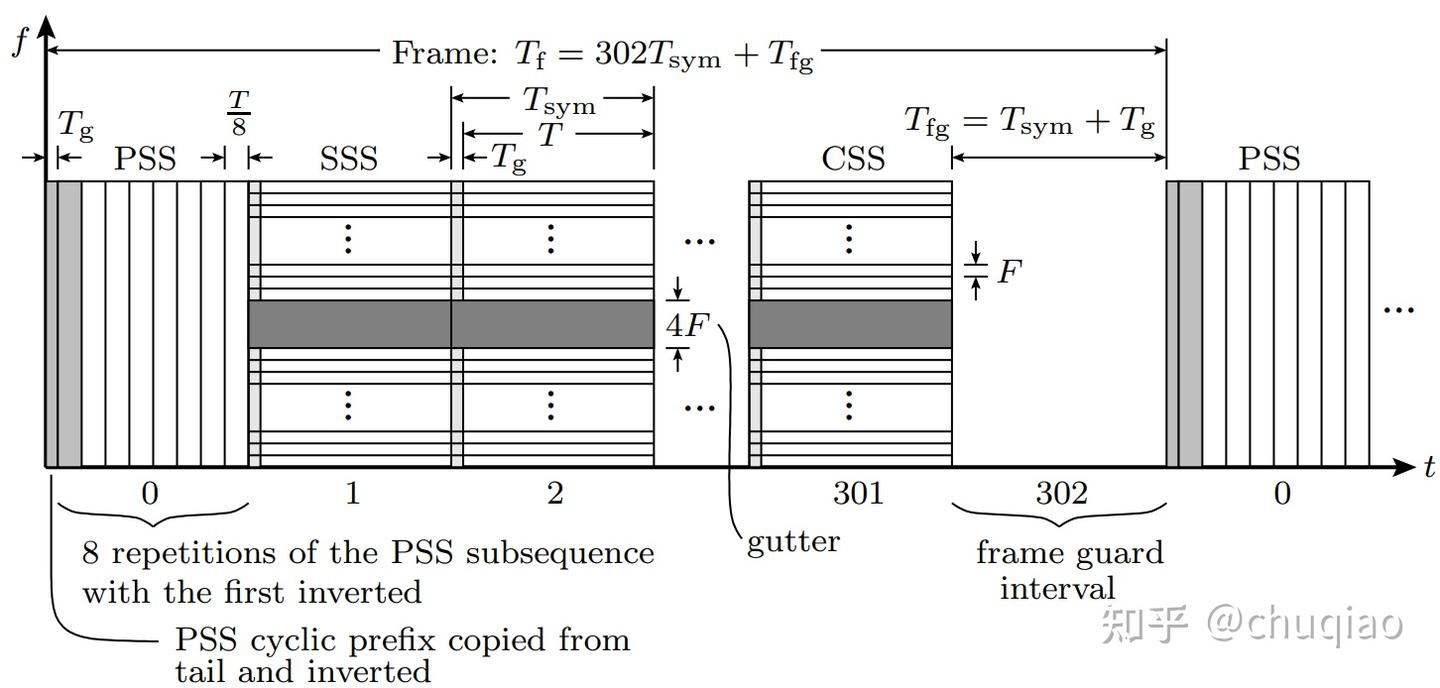
图6 Ku波段Starlink下行链路沿时频维度的帧布局

1. 帧布局
   如图6所示。每帧由302个间隔组成，每个间隔加上帧保护间隔Tfg，长度Tsym =4.4μs，总帧周期为Tf =1/750s。每一帧都以PSS开始，它在本地时域中表示，其次是SSS，其格式为标准4QAM OFDM符号。每一帧以CM1SS结尾，后跟CSS和帧保护间隔。后续帧是否存在，取决于用户需求。
   SSS和CSS的已知信息符号允许接收机，用于对在每个帧的开头和结尾所有子载波执行信道估计，允许在帧内插值。在CSS之前的CM1SS，仅部分填充从每帧重复的信息符号，它的目的暂不清楚，但其可预测的元素无疑也可用于信道估计。
   在每一帧中，带有索引i∈{2,3,4,5}的OFDM符号似乎包含标头(控制平面)信息—可能包括卫星、频道和调制调度。我们从符号i =5和i =6之间突然的90度星座方向的偏移，可以解释为表示从标头到有效负载符号的过渡。这种方向的转变可以在图4的左右部分之间看到。前七个左右的有效载荷符号(从i =6到大约i =12)有时是16QAM调制，其余符号是4QAM调制。我们假定16QAM符号是发给用户的，其接收的SNR足以支持解码 (约15dB，取决于信道编码)。
   前面提到的4F宽的中信道暗沟是存在于帧中包含的所有OFDM符号中，但不存在于PSS中。
2. 同步顺序
   同步序列对于努力为PNT提供两用的Starlink信号特别重要。民用GNSS信号的扩频码，同步序列可以通过无源(仅接收)无线电预测从而用于构建一个本地信号副本，其与收到的信号相关性接产生标准伪距和多普勒可观察物，是PNT的原始成分。

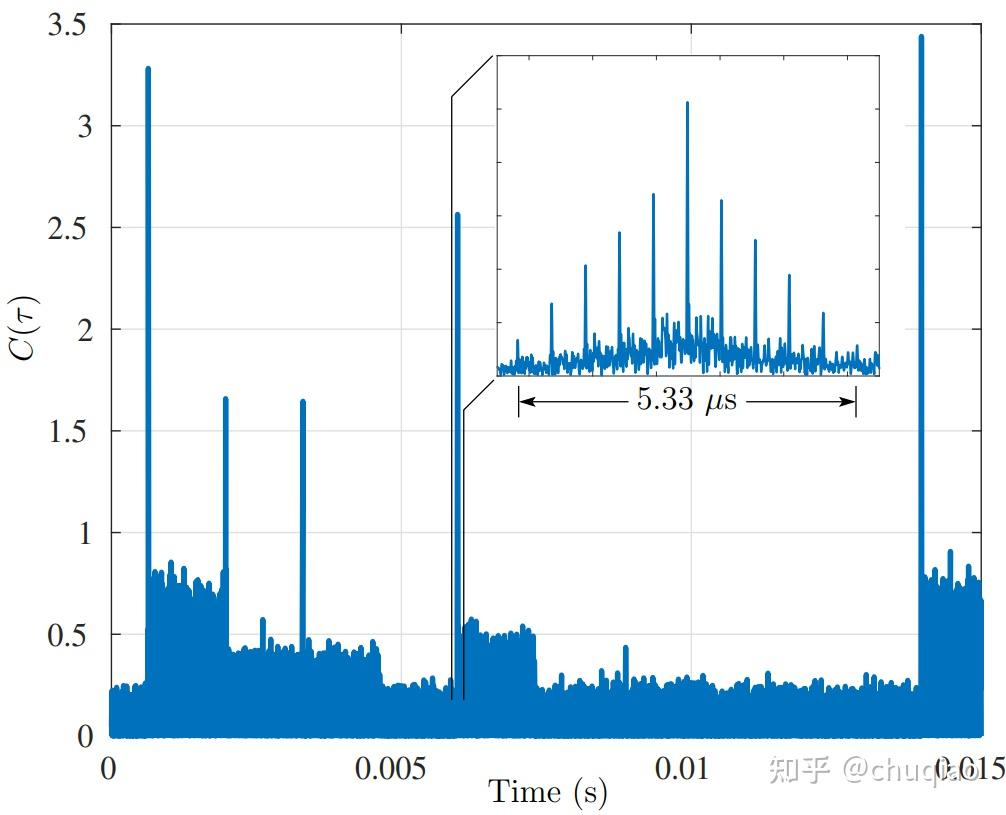
图7：多普勒补偿后的窄带模式接收的Starlink数据与本地PSS副本的相关性
图7显示，每帧的开头与PSS的相关性，产生尖锐的峰值。图7插图中显示的11齿梳子的独特形状源于组成 PSS 的子序列(pk)2N/8−1k =N/8的重复和反转。请注意，从相同的卫星和波束接收相邻帧有不同的功率，证明该系统在一个服务小区中采用用户子集相关的功率适配方案。还要注意在某些间隔内没有帧，这表明用户数据需求远低于显示间隔内的系统容量。然而应该指出，贯穿我们研究的整个数据间隔，帧占用率从未低于1/30(每40ms一帧)。我们直觉认为，源源不断但稀疏的帧，是支持初始入门级网络所必需的。因此，即使在用户需求很少或没有用户需求的期间，来自每颗卫星的帧到达都是规则和密集的，足以支持机会主义的PNT。
重要的是，每帧都保持相位相干性，帧和卫星之间与同步序列之间的相位关系似乎是恒定的。这意味着同步序列的时域表示 (带有各自的循环前缀)可组合，以延长相干积分间隔超过一帧，来提高接收机灵敏度和可观察的测量精度。该技术可以在低于-6dB SNR时产生伪距和多普勒可观测值，低于支持通信所需的SNR。因此利用Starlink进行PNT的接收机不需要配备高增益天线，甚至可以提取来自不为其所在小区提供服务的卫星的可观测量。
然而，与GNSS扩频码不同，Starlink同步序列并非每颗卫星所独有。这带来了卫星分配歧义问题，必须根据近似用户位置、已知卫星星历表和测量的多普勒和帧到达时间等数据组合求解。
似乎很清楚为什么PSS由重复子序列组成：在高SNR条件下，通过与单个PSS子序列相关联，然后采用具有最大模量的复累加的FFT来完善多普勒估计，可以更有效地搜索（29）所需的初始网络进入的多普勒和帧开始时间。较短的初始相干积分区间更能容忍β的误差。如果由于单序列相关SNR不足而失败，多子序列可以相干累积，速度较慢但搜索更敏感。
鉴于出色的自相关性质[24]，PSS基于m序列也是合乎逻辑的。与常规二进制编码相比，将m序列编码为一系列π/2相移更能减少频谱泄漏。对PSS进行差分编码的原理不太清楚。已知对称DPSK提高对多普勒数据解调的鲁棒性，以及卫星通信中常见的定时不确定性[25]。但这不适用于与频率和时间同步的已知PSS（或其部分）的相干相关性。最有可能的是，差分编码旨在提供一种额外的方法来平衡搜索灵敏度以提高效率
我们无法将SSS识别为规范序列。其频域复系数表现出良好的自相关特性，但不像m序列或用于LTE中PSS的Zadoff-Chu序列的恒定幅度零自相关性。我们怀疑SSS可能是两个加扰m序列的混合，就像LTE的SSS一样。

1. 容量差距
   检查Starlink信号结构很有趣的是其设计裕量的条款。它的设计者如何以通信的数据吞吐量为代价平衡可靠性和成本？
1. 频谱占用：信道之间的10MHz保护带将Starlink的频谱占用率降低到Fs/Fδ =24/25。在信道之间留下如此宽的未使用带宽，这相当于超过42个子载波间隔，表明Starlink打算一次激活多个频道给定的服务小区，并希望通过降低采样率和RF滤波要求保持较低的UT成本。
2. OFDM符号占用率：有用符号间隔到完整OFDM符号间隔的比率为T/Tsym =N/(N+Ng) =32/33，这反映了相当有效的设计。与LTE相比，其N/Ng范围为12.8(效率更高)到4(延迟扩散的余量更大)，Starlink的比率为32。显然，Starlink设计者正在利用空地信道中传播的低延迟扩散。即便如此，Tg =Ng/Fs =130ns超过最坏情况下的Ku波段的延迟扩展95%均方根值，在[20]中找到是Td =108ns。
3. 帧占用：可以查看帧占用 NsfdTsym/Tf =298/303.03。如果索引为i∈{2,3,4,5}的OFDM符号，似乎包含标题信息，则占用率变为294/303.03。专用于同步序列的OFDM符号间隔数 (每1.33毫秒4个)，与地面OFDM波形相比更高。例如，LTE每5毫秒传输一次两个同步序列。通过每个帧尾两个同步序列，Starlink设计者确保UT可以执行异常高精度的信道均衡和多普勒(CFO)估计。这减少了帧占用，但预示着双重用途PNT的Starlink信号：更大比例的可预测元素，面向PNT的接收机可以相干地积分越长时间，从而在更低SNR下产生伪距离和多普勒可观察量。
4. 信道占用：由于4F宽的暗沟，信道占用最多为(N−4)/N =1020/1024，但是可能略低：除了显示同步序列的位置，第5-G节中描述的逐符号逐帧相关性分析表明，导频子载波上存在具有可预测的信息符号的间歇性调制。

 

信道占用的另一个衡量标准是子载波间距。回想一下，Fs中的子载波N的数量必须为2的幂才能进行高效的OFDM处理，并且(12)中的其他条件，dOFDM随着N的增加而上升。Starlink设计者可以选择N =2048而不是N =1024，因此F缩小了2倍并且dOFDM增加了1.54%？可能是这样：假设Nsync=210(比PSS中的样本更少)和SNR =5dB(用于4QAM解码的阈值，假设良性信道和强编码)，N =2048可以轻松满足约束(15)。

1. 结论
   我们开发并应用了盲信号识别技术，来揭示Starlink Ku波段下行链路信号的频域和时域结构。我们进一步确定了四个同步序列，可被动的利用Starlink信号进行伪距离定位，导航和计时(PNT)，并明确评估了两个其中。本文的结果阐明了使用Starlink信号，作为传统GNSS进行PNT备份的路径。
2. 参考文献

[1] T. G. Reid, A. M. Neish, T. Walter, and P. K. Enge, “Broadband LEOconstellations for navigation,” Navigation, Journal of the Institute ofNavigation, vol. 65, no. 2, pp. 205–220, 2018.

[2] T. G. R. Reid, T. Walter, P. K. Enge, D. Lawrence, S. Cobb, G. Gutt,M. O’Connor, and D. Whelan, Position, Navigation, and Timing Technologiesin the 21st Century: Integrated Satellite Navigation, SensorSystems, and Civil Applications. Wiley-IEEE, 2020, vol. 1, ch.Navigation from Low Earth Orbit: Part 1: Concept, Capability, andFuture Promise., pp. 1359–1380.

[3] Z. M. Kassas, Position, Navigation, and Timing Technologies in the21st Century: Integrated Satellite Navigation, Sensor Systems, and CivilApplications. Wiley-IEEE, 2020, vol. 1, ch. Navigation from Low EarthOrbit: Part 2: Models, Implementation, and performance, pp. 1381–1412

[4] N. Jardak and Q. Jault, “The potential of LEO satellite-based opportunisticnavigation for high dynamic applications,” Sensors, vol. 22, no. 7,p. 2541, 2022

[5] P. A. Iannucci and T. E. Humphreys, “Fused low-earth-orbit GNSS,”IEEE Transactions on Aerospace and Electronic Systems, pp. 1–1, 2022

[6] M. Neinavaie, J. Khalife, and Z. M. Kassas, “Exploiting Starlink signalsfor navigation: First results,” in Proceedings of the ION GNSS+ Meeting,St. Louis, Missouri, Sept. 2021, pp. 2766–2773

[7] ——, “Acquisition, doppler tracking, and positioning with starlink LEOsatellites: First results,” IEEE Transactions on Aerospace and ElectronicSystems, vol. 58, no. 3, pp. 2606–2610, 2022

[8] J. Khalife, M. Neinavaie, and Z. M. Kassas, “The first carrier phasetracking and positioning results with Starlink LEO satellite signals,”IEEE Transactions on Aerospace and Electronic Systems, vol. 58, no. 2,pp. 1487–1491, 2022

[9] SpaceX, “Revised SpaceX Gen2 non-geostationary satellite system,Technical Attachment,” https://licensing.fcc.gov/myibfs/download.do?attachment key=12943362, Aug. 2021, SAT-AMD-20210818-00105

[10] A. Bouzegzi, P. Ciblat, and P. Jallon, “New algorithms for blindrecognition of OFDM based systems,” Signal Processing, vol. 90, no. 3,pp. 900–913, 2010

[11] A. Gorcin and H. Arslan, “An OFDM signal identification methodfor wireless communications systems,” IEEE Transactions on VehicularTechnology, vol. 64, no. 12, pp. 5688–5700, 2015

[12] M. S. Chaudhari, S. Kumar, R. Gupta, M. Kumar, and S. Majhi, “Designand testbed implementation of blind parameter estimated OFDMreceiver,” IEEE Transactions on Instrumentation and Measurement,vol. 71, pp. 1–11, 2021

[13] M. L. Psiaki, “Navigation using carrier Doppler shift from a LEO constellation:TRANSIT on steroids,” Navigation, Journal of the Instituteof Navigation, vol. 68, no. 3, pp. 621–641, 2021

[14] L. Cimini, “Analysis and simulation of a digital mobile channel usingorthogonal frequency division multiplexing,” IEEE transactions oncommunications, vol. 33, no. 7, pp. 665–675, 1985

[15] W. Y. Zou and Y. Wu, “COFDM: an overview,” IEEE transactions onbroadcasting, vol. 41, no. 1, pp. 1–8, 1995

[16] J. Armstrong, “OFDM for optical communications,” Journal of lightwavetechnology, vol. 27, no. 3, pp. 189–204, 2009

[17] A. Ancora, I. Toufik, A. Bury, and D. Slock, LTE–The UMTS LongTerm Evolution: From Theory to Practice. Wiley, 2011, vol. 1, ch. 5:Orthogonal Frequency Division Multiple Access (OFDMA), pp. 123–143

[18] J. Proakis and M. Salehi, Digital communications 5th Edition. McGraw-Hill, 2007

[19] T. Jiang and Y.Wu, “An overview: Peak-to-average power ratio reductiontechniques for ofdm signals,” IEEE Transactions on broadcasting,vol. 54, no. 2, pp. 257–268, 2008

[20] E. L. Cid, M. G. Sanchez, and A. V. Alejos, “Wideband analysis of thesatellite communication channel at Ku-and X-bands,” IEEE Transactionson Vehicular Technology, vol. 65, no. 4, pp. 2787–2790, 2015

[21] T. Hobiger, D. Piester, and P. Baron, “A correction model of dispersivetroposphere delays for the ACES microwave link,” Radio Science,vol. 48, no. 2, pp. 131–142, 2013

[22] O. A. Dobre, “Signal identification for emerging intelligent radios:Classical problems and new challenges,” IEEE Instrumentation & MeasurementMagazine, vol. 18, no. 2, pp. 11–18, 2015

[23] D. Rife and R. Boorstyn, “Single tone parameter estimation fromdiscrete-time observations,” IEEE Transactions on information theory,vol. 20, no. 5, pp. 591–598, 1974

[24] E. H. Dinan and B. Jabbari, “Spreading codes for direct sequence cdmaand wideband cdma cellular networks,” IEEE communications magazine,vol. 36, no. 9, pp. 48–54, 1998

[25] J. Winters, “Differential detection with intersymbol interference andfrequency uncertainty,” IEEE Transactions on Communications, vol. 32,no. 1, pp. 25–33, 1984.

编辑于 2023-06-21 10:28・IP 属地北京

 

============= End