7天算法训练营体验课 —— 极客大学

刚发现讲课的覃超大佬之前在知乎上就关注他很久了。。。果然大佬做什么都很厉害啊，自己还得加油！！！

7天算法训练营体验课

1. 时间和空间复杂度

1.1 时间复杂度

Big O notation

O(1): Constant Complexity 常数复杂度
O(log n): Logarithmic Complexity 对数复杂度
O(n): Linear Complexity 线性时间复杂度
O(n^2): N Square Complexity 平方
O(n^3): N Cubic Complexity 平方
O(2^n): Exponential Growth 指数
O(n!)

TIPS：只看最高复杂度的运算，且不考虑前面的系数

示例：

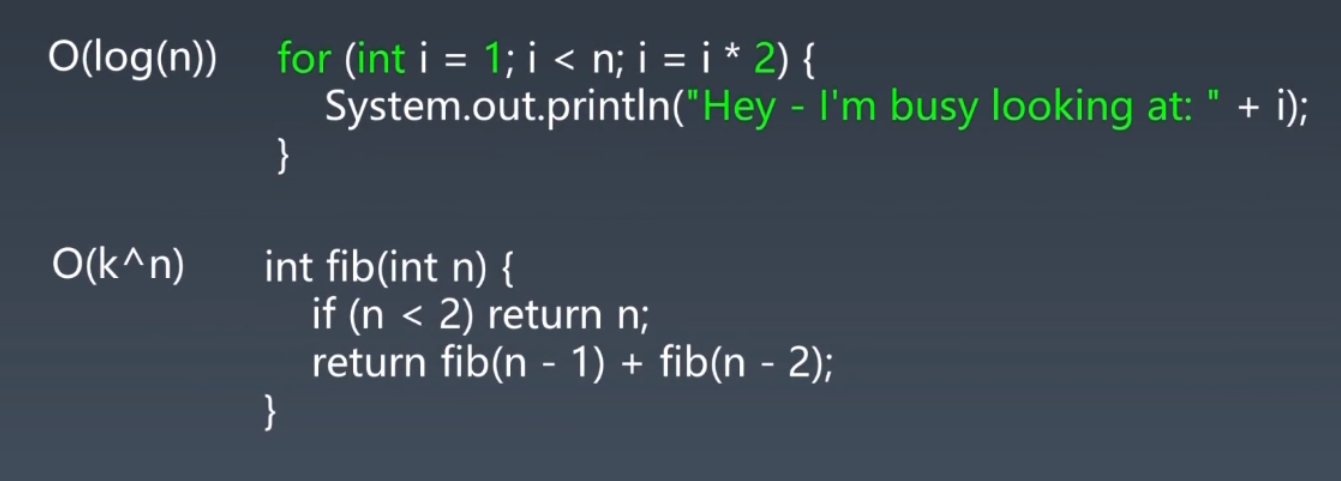
第一个：如果 n = 4，则执行2次，即永远会执行 $$log_2n$$ 次！所以时间复杂度为：O(logn)
第二个：求斐波拉契数列，递归程序，非常慢指数级时间复杂度。所以时间复杂度为：O(k^n)

时间复杂度曲线

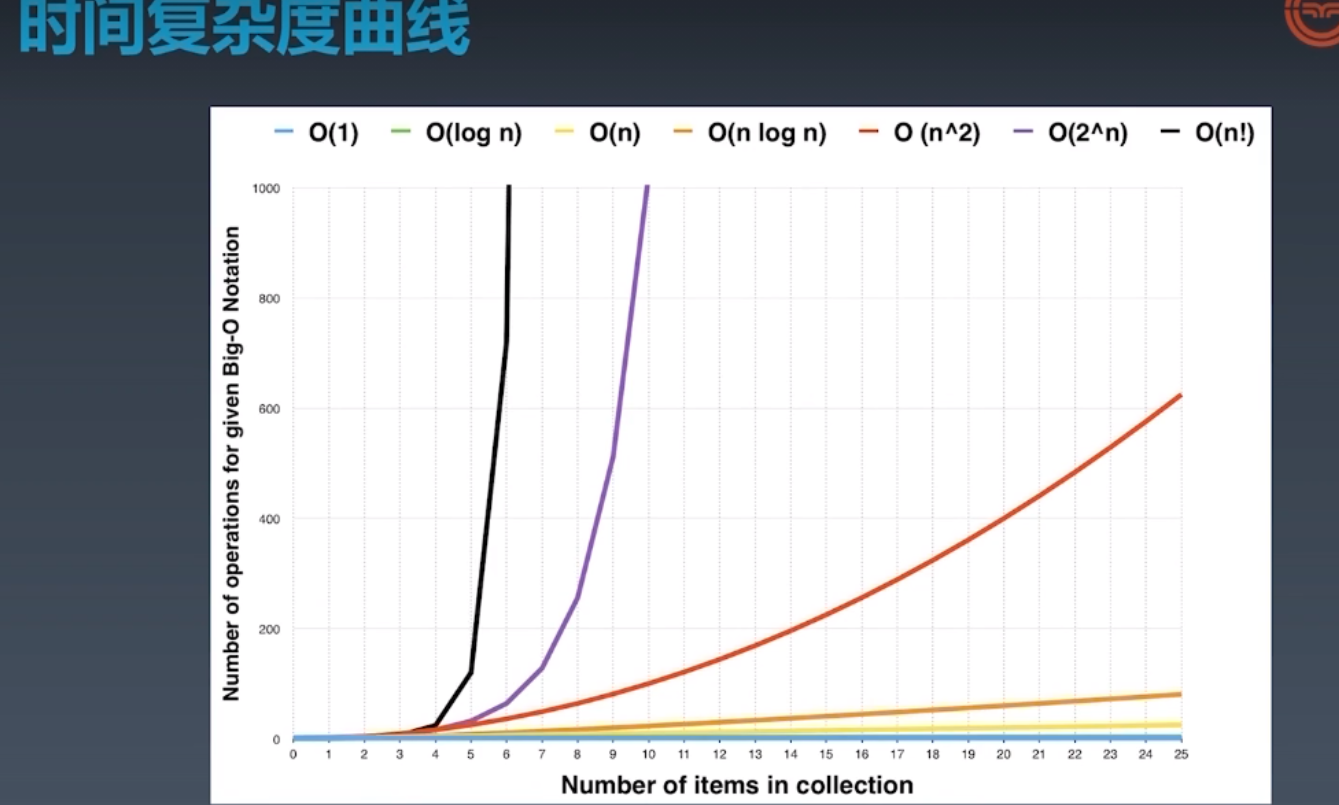
所以一定要对自己程序的时间、空间复杂度有要求！

面试结题步骤四件套：

和面试官确认题目意思，准确无误
想所有可能的解决办法，同时比较这些方法的时间、空间复杂度
挑选其中最优解决方法：时间复杂度最低的方法，内存占用也尽可能低
测试写的代码

+++

时间复杂度分析 更复杂的情况：递归

需要了解总共递归执行了多少次 -> 把递归的执行顺序画成树形结构，递归状态的递归树/状态树

示例：斐波拉契数列 Fib 0，1，1，2，3，5，8，13，21

递归公式： f(n) = f(n-1) + f(n-2)

面试（直接用递归）

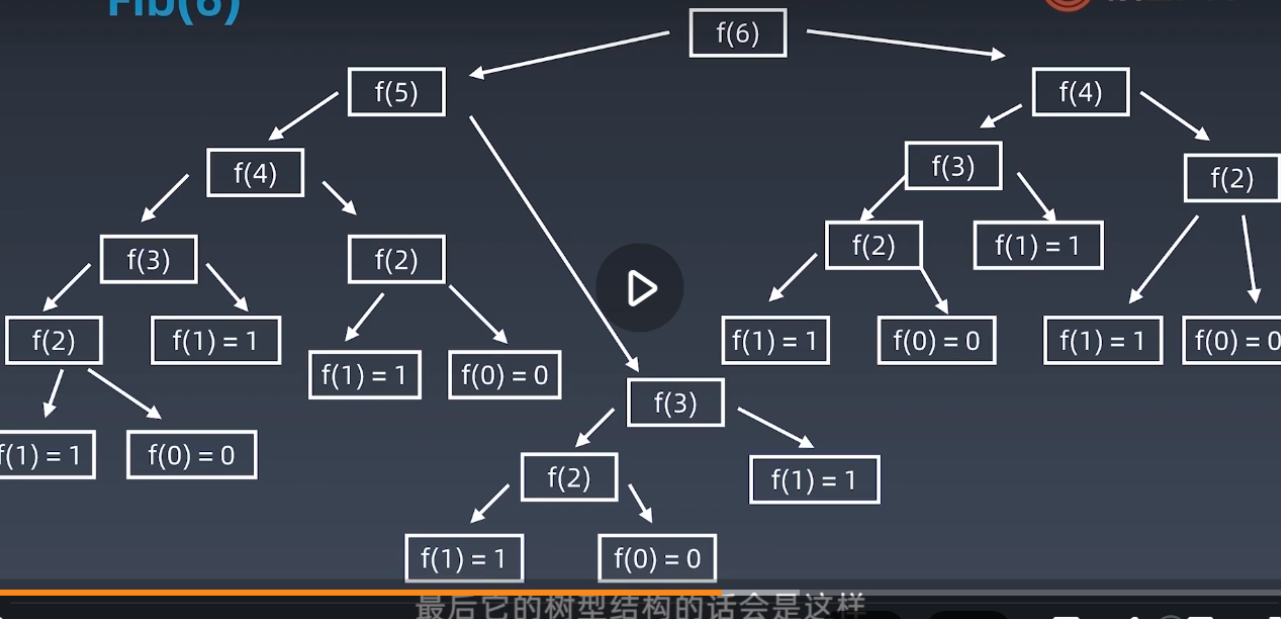
int fib(int n){
    if (n < 2) return n;
    return fib(n-1) + fib(n-2);
}    // 时间复杂度；O(k^n) or O(2^n)
	 // 一定不要这么写！！除非加上缓存中间结果，或者用循环来写

最后的树形结构如下：

观察：每一层的节点数上一层的两倍，所以O(2^n)。

主定理 Master Theorem，用来分析递归的时间复杂度

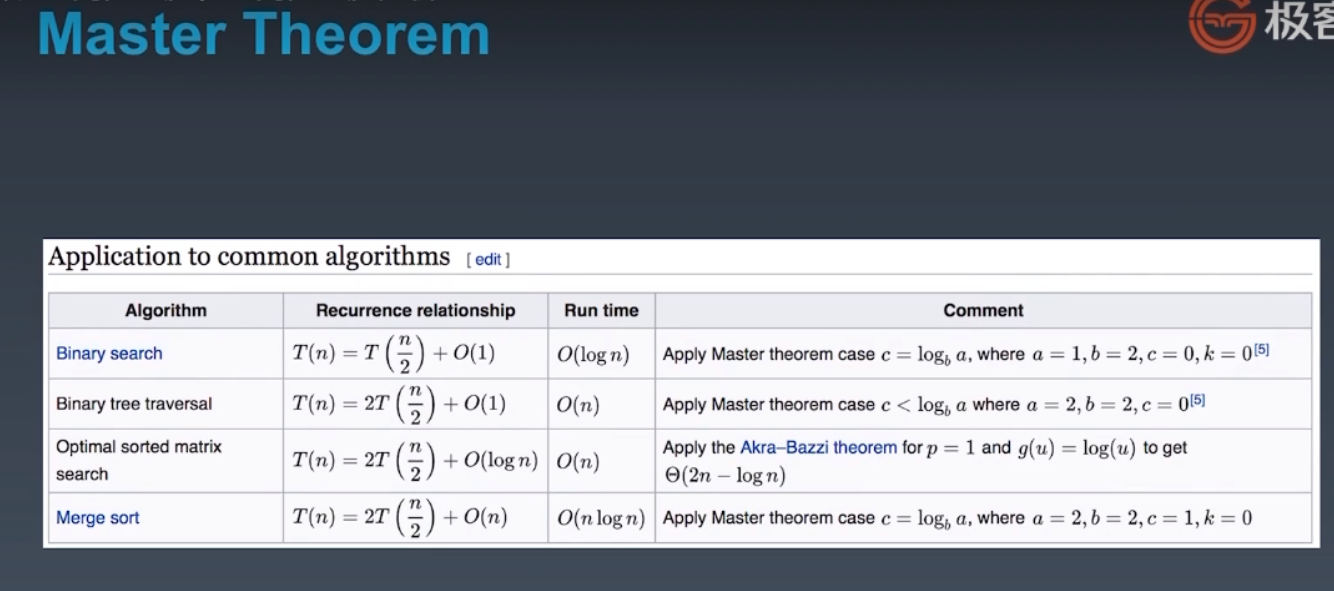
二分查找：一般应用于（一维）有序数列中寻找目标数，时间复杂度：O(log n)
二叉树遍历：每个节点都会被访问一次，且仅被访问一次。时间复杂度：O(n)
排好序的二维矩阵中进行二分查找：时间复杂度O(n)
归并排序：最优的排序时间复杂度也是时间复杂度O(nlogn)

示例：

第一、第二、第三个：时间复杂度都是O(n)，n为节点总数。

第四个：时间复杂度为O(logn)

1.2 空间复杂度

空间复杂度：除了原本的数据以外，建立算法需要新开辟的空间大小

对于空间复杂度，一般来说：

程序中开了新的数组，数组的长度基本上就是空间复杂度，例如：n为传入元素个数时，新开一个一维数组O(n)，二维数组O(n^2)
有递归的话，递归最深的深度，就是空间复杂度的最大值
新开数组和递归都存在时，两者之间的最大值就是空间复杂度

示例：leetcode 爬楼梯 https://leetcode-cn.com/problems/climbing-stairs/

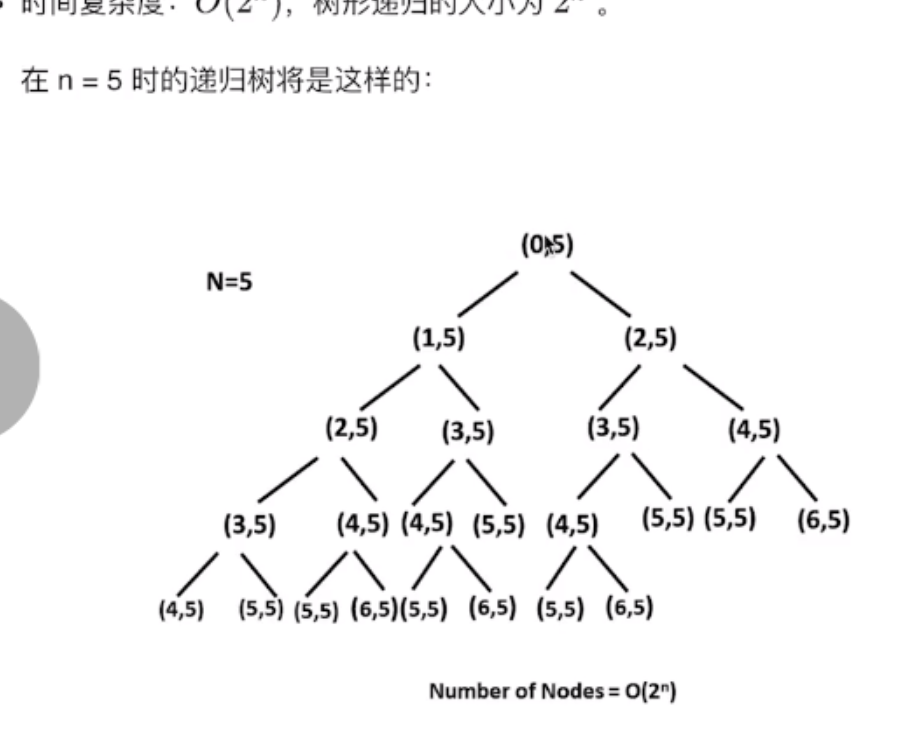
1. 使用递归的斐波拉契数列来解，且没有缓存。时间复杂度：O(2^n)，空间复杂度：O(n)，因为左边每次 - 1，最多n层
1. 记忆化递归：加入了内存数组 memo，中间结果会保留，使得递归的时间复杂度变为O(n)；新开了一个数组长度为n，所以空间复杂度还是O(n)
1. 动态规划：开了个一维数组 dp 长度为n，空间复杂度为O(n)，时间复杂度O(n)
1. 继续内存上优化递归：因为无需存所有的中间结果，只需存 i-1 和 i-2的结果，所以不再申请数组，而是申请两个中间变量！！！再加上第三个变量即可以递归！！所以空间复杂度为O(1)，时间复杂度O(n)

2. 数组、链表、跳表的基本实现和特性

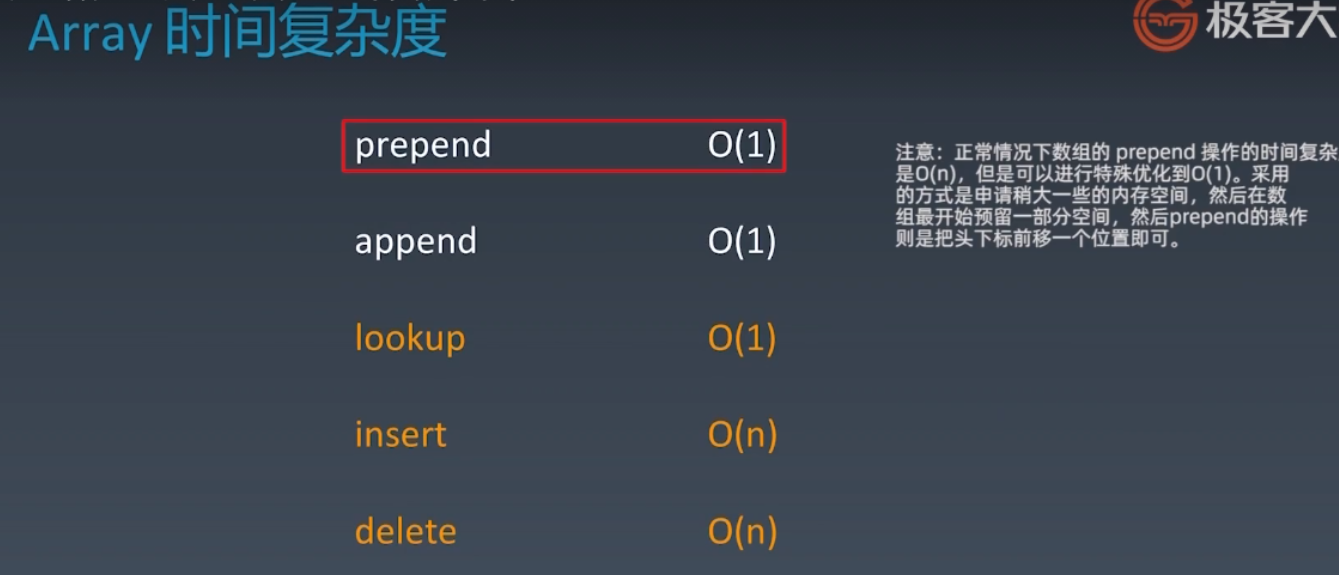
2. 1 数组 Array

底层：开辟连续的内存地址，随机访问的时间复杂度O(1)

插入、删除时间复杂度O(n)

2.2 链表 Linked List

为了弥补数组添加、删除操作时不够高效的缺点，引入链表

每个元素一般用class来定义，可以叫做node。里面包含两个成员变量：value，next 指针/引用
添加 prev 指针/引用，变成双向链表
头、尾指针分别叫 head 和 tail，tail -> next = null。如果不为空，而是指向头节点，则是循环链表。

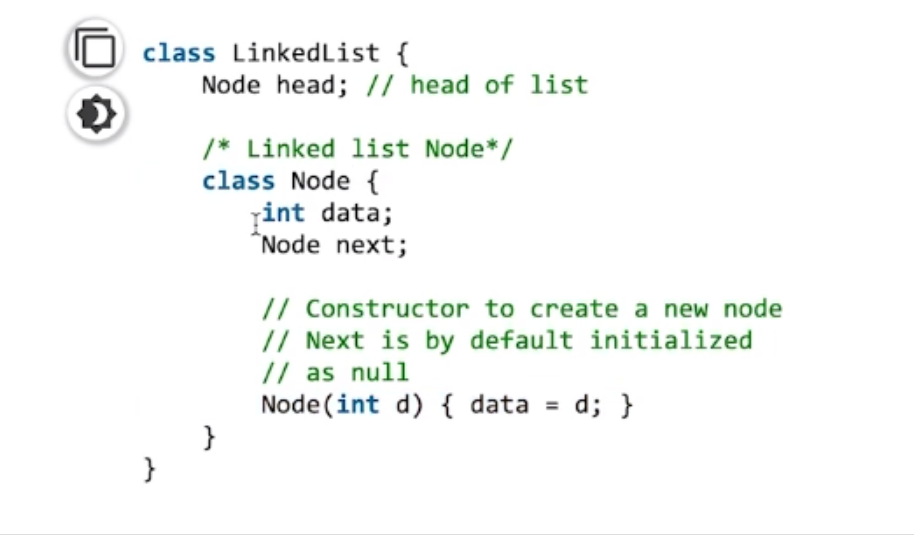
简单实现，链表和Node都是一个 class

Java源码中 LinkedList 是一个标准的双向链表结构！

链表的插入、删除时间复杂度O(1)，没有复制、移动的操作，但是随机访问操作O(n)

2.3 跳表 Skip List

问题背景：链表有序时，如何加速（查找操作）？ PS：不能用数组的二分查找

跳表中的元素都必须是有序的
插入/删除/搜索都是：O(logn)
用来替代平衡树（AVL Tree）、二分查找，例如用于Redis、LevelDB

一维数据结构要加速，通常要升维：可理解为多一级维度，则多一级信息

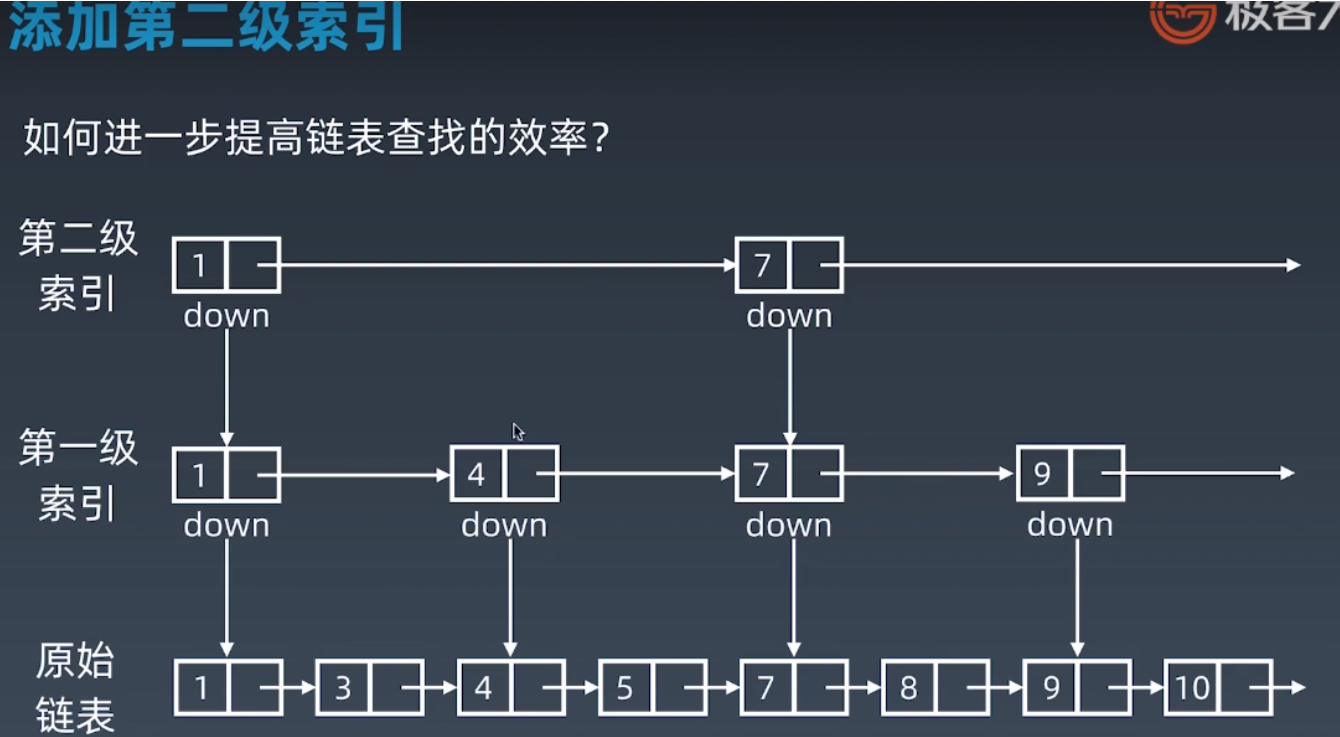
依此类推，可以增加多级索引

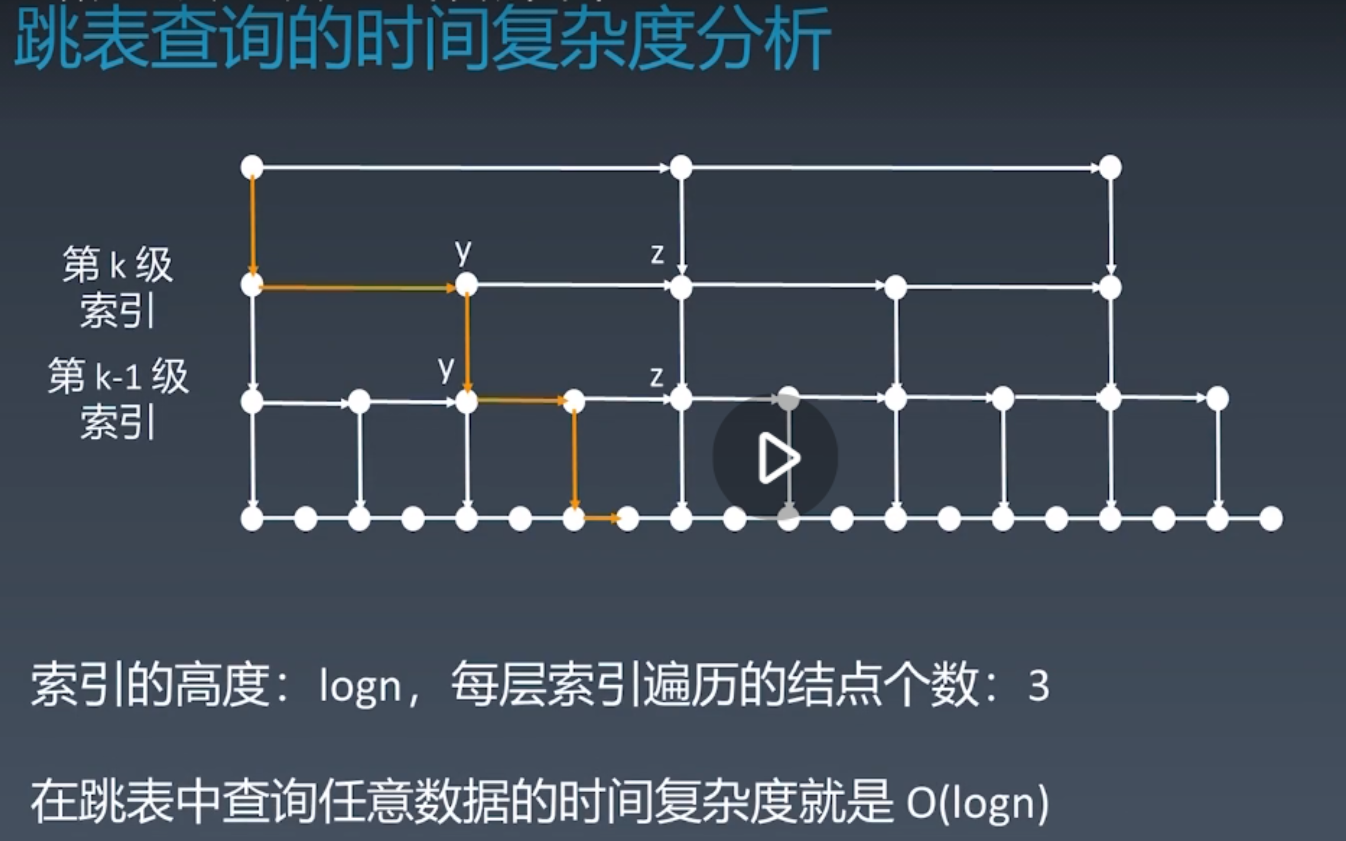
分析：记住结论，查询的时间复杂度O(logn)

现实中的跳表：

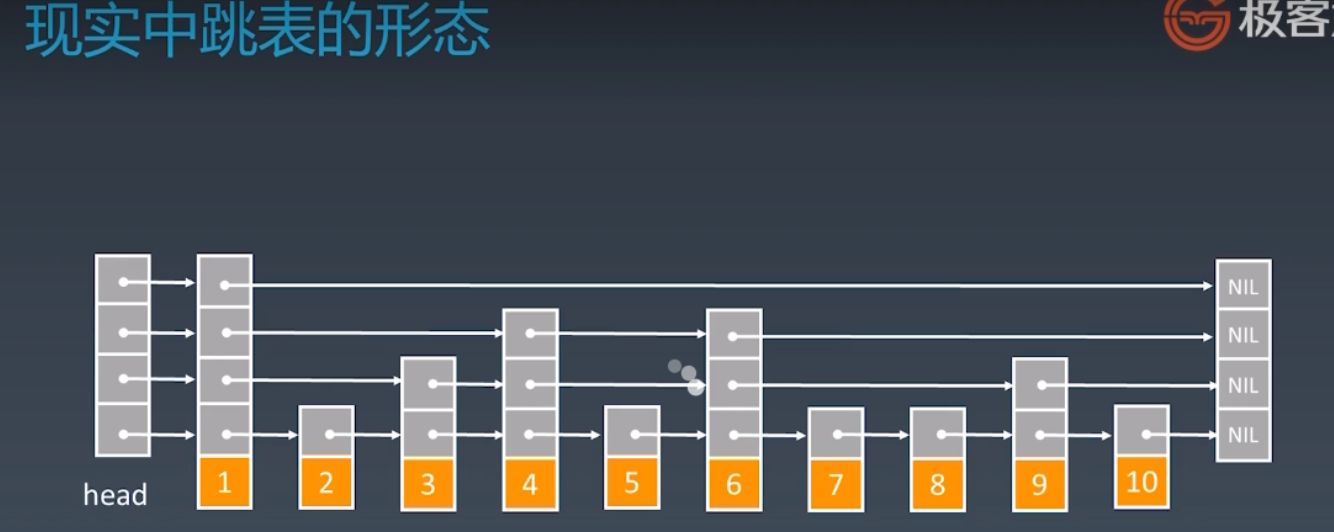
由于有元素被删除，所以索引不是很平均
同时，维护成本相比链表更高，增加、删除元素也需要更新索引，所以时间复杂度上升为O(logn)

跳表的空间复杂度

最后会收敛，所以空间复杂度还是O(n)这个数量级，不过比原始的链表肯定复杂度高不少。

2.3 工程运用

Linked List在工程中应用很多，许多语言都有封装好的高级数据结构。

LRU Cache：http://leetcode-cn.com/problems/lru-cache 用Double Linked List就可以实现了
Redis：使用跳表，http://redisbook.readthedocs.io/en/latest/internal-datastruct/skiplist.html

http://www.zhihu.com/question/20202931

面试不会要求手写跳表，而是看文章理解概念和运用

+++

2.4 小结

2.5 实战题目解析：移动零

五毒神掌：
练题步骤：

1.5-10 分钟：读题和思考
2.有思路：自己开始做和写代码，不然，马上看题解
3.默写背诵，熟练
4.然后开始自己写（闭卷）

写出自己想到的所有解法，不需要考虑时间复杂度和空间复杂度

Leetcode 上执行代码
可以修改测试用例

提交代码
查看执行结果，查看执行用时，内存消耗不太重要

查看别人的解法：
对于不好的解法可以直接略过
对于写的好的解法，可以自己按照这个解法，改进的自己的解法，也可以直接拿过来，但是需要自己整理下

最大的误区，刷题只刷一遍
核心的思维：升维，空间换时间
刷题五遍

在中国网上看完之后，去国际站看看

数组题目：

3. 树、二叉树、二叉搜索树的实现和特性

回顾：

一维结构数据结构，如链表，缺点查询O(n) -> 提出跳表，查询O(logn)
如果要加速，通常可以考虑升维，例如链表next节点不止一个，就变成了树 Tree

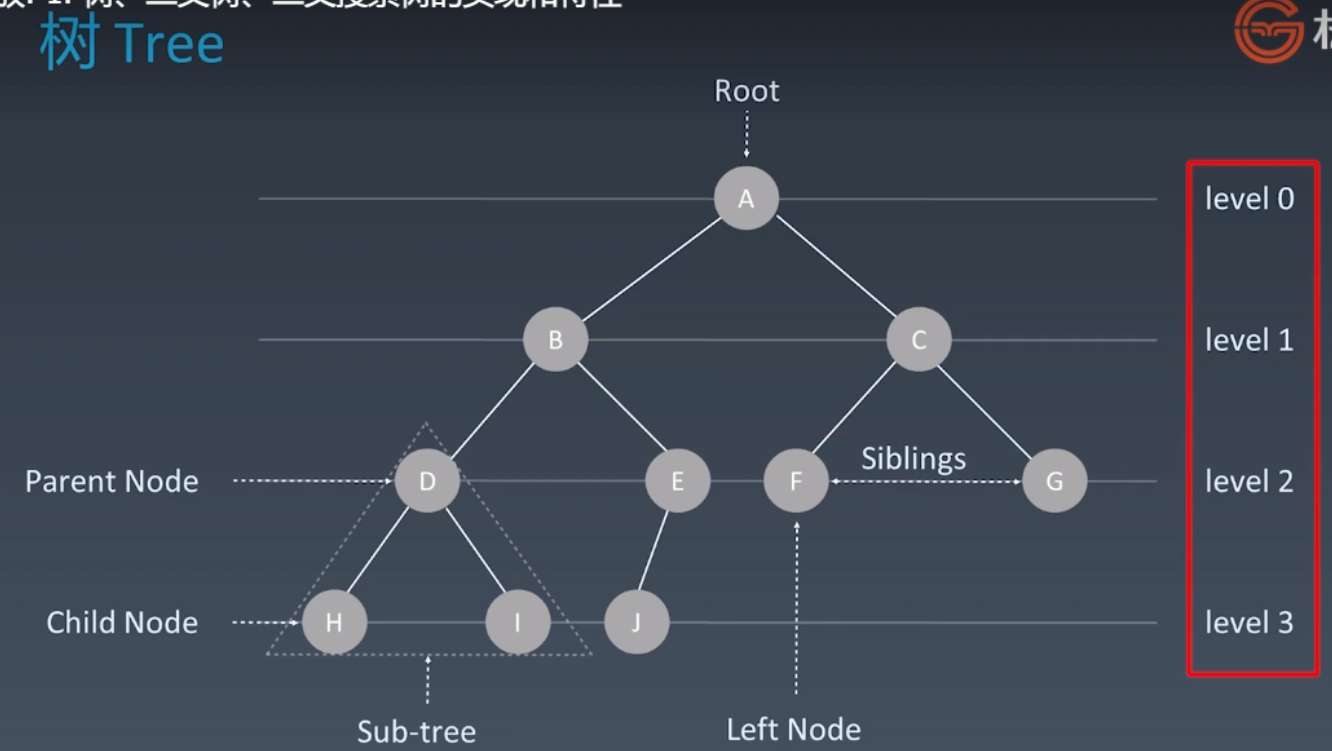
最常用：二叉树

PS：树和图：图可能有环

节点示例代码：

3.1 二叉树的遍历

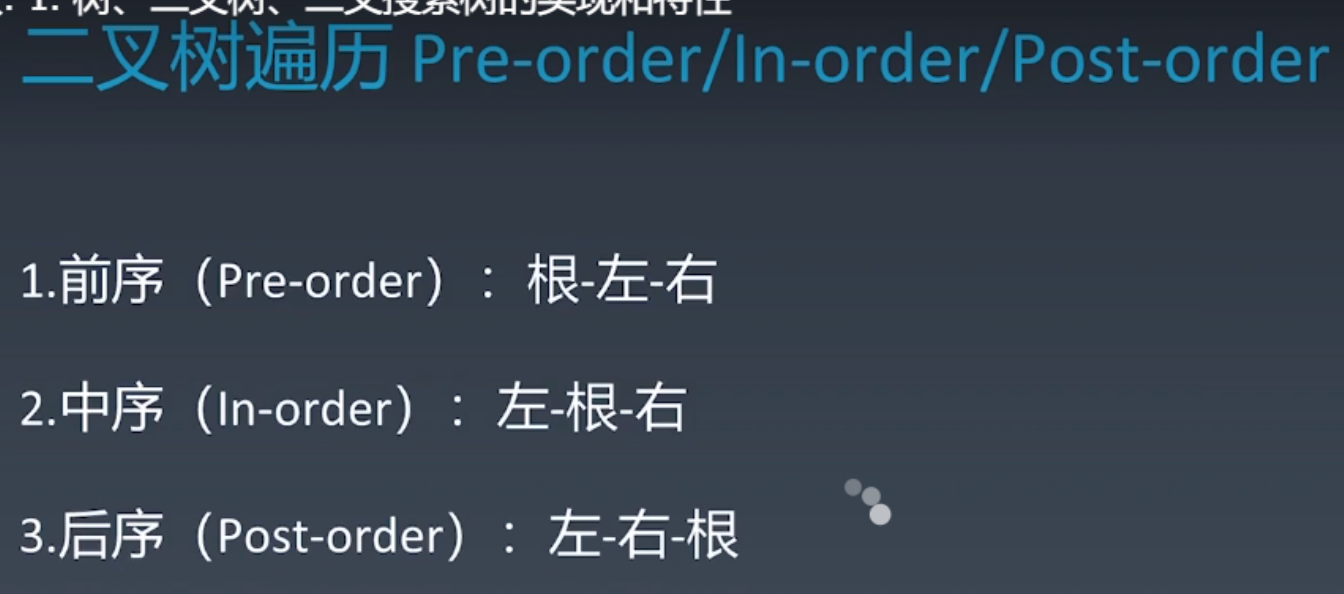
前、中、后序遍历示例代码：

PS：树的遍历通常是递归，算法复杂度O(n)，形式漂亮，且不好写循环。

二叉搜索树 Binary Search Tree

是左、右子树的所有节点均小于根节点，而非只有左、右子节点。
空树也是二叉搜索树。

操作时间复杂度都是O(logn)，相对遍历O(n)加速了很多
插入等价于：先做查询，最后查询到的位置就是应该插入的位置！
创建一颗二叉搜索树等价于：从一颗空树开始，不停调用插入操作，将所有节点依次插入
在叶子上，直接删除即可；如果是中间节点、根节点，则从要删除的节点出发，找一个最接近它且比它大的节点（即被删节点右子树中最小的节点），将其替换到这个位置
最差情况 Worst：二叉树只有右节点，即变成了一个单链表，此时所有操作都退化到了O(n)时间复杂度。此时需要配平，变成平衡二叉树。

3.2 实战题目解析：二叉树的中序遍历

思考：为什么树的面试题解法一边是递归？

原因：

树没有一个清晰的后续结构，即适合for、while等循环的结构。而每个节点都有自己的左右叶子节点，那么需要访问子树的话，只要不断递归调用相同的遍历函数。
节点的定义就是用递归的方式进行的。
结构有重复性（自相似性）。

前中后序遍历代码记住，需要脱离PPT也能写出来

实战题目：

第五题是广度优先遍历

递归等于系统帮你创建一个栈，所以解法中也有自己维护一个栈结构来做遍历。
莫里森遍历，不是必考。
不需要刻意规避使用递归，可以将递归和循环效率视作一样。要避免的是不理解递归把代码写残了，例如求斐波拉契数列使用递归，但是不缓存中间结果，使得线性可解决的问题复杂度变高了。

4. 递归

4.1 递归的实现、特性以及思维要点

见3.2

PS：《盗梦空间》

简单例子：求阶乘

递归调用栈

Python递归代码模板

递归函数分为四部分：

1.终止条件 Terminator，一定先写好！防止无限递归、死循环
2.处理当前层逻辑代码 Process Current Level Logic
3.下探到下一层 Drill Down，level用来标记当前层数，p1等是需要下放的参数
4.清理当前层 Reverse States（有时需要）

PS：Java模板

思维要点

1. 刚开始学可以人肉图上画一画，后面记住代码抛弃人肉递归
1. 可能问题逻辑很复杂，需要找到最近重复性，那么就可以通过少行数的递归代码来完成
1. 当n=1，2成立，且假设n成立时可以推出n+1成立

4.2 实战题目解析：爬楼梯、括号生成等问题

基本上递归代码面试题都在二十行以下，所以肯定不要死写。

示例：爬楼梯

找重复性，用数学归纳法思想：直接思考n比较难，那就先n=1，2
重要：当n=3时，可以理解成n=1的楼梯走法，再跨两步走到n=3；或者n=2的楼梯走法，再跨一步走到n=3，那么n=3的总走法f(3) = f(1) + f(2)！！！实现了 mutual exclusive, complete exhaustive
那么同样的n=4时的总走法f(4) = f(3) + f(2)
最后抽象出来，即斐波拉契数列 f(n) = f(n-1) + f(n-2)，可以理解成：要走到第n级楼梯，那么只能从n-1级楼梯跨1步上来，或者从n-2级楼梯跨两步上来，没有其他可能性。
转化成求斐波拉契：
- （1）傻递归，时间复杂度太高，O(2^2)
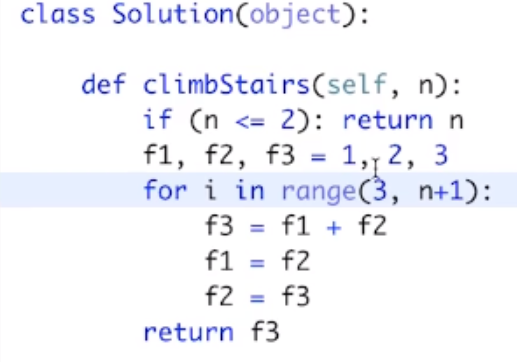
- （2）动态规划：如下

示例：括号生成

人肉递归很难，n=4可能就晕了
适合程序递归

思考过程：

题目等价于：有2n个格子（例如n=3，有6个格子），其中可以放左括号/右括号（不考虑合法性的话），问如何产生全部的可能结果？
写递归代码：先把模板的四步都写下来！（用备注即可）
- Terminator：level <= max
- Process Current Level Logic: 生成左/右括号（PS：此处可以把操作直接放到drill down的参数列表中，不用新建变量来存处理结果）
- Drill down: 将两个结果都放入递归函数
- Reverse States: 都是局部变量，没有动全局变量
此时，代码会产生所有6个括号的可能结果（穷举），没考虑合法性，接下来就是加入判断合法性的条件。当然，此题目最合适的是在生成可能结果时就加入判断条件：
- 左括号 left：只要不超标<=n，随时可以加
- 右括号 right：左括号个数>右括个数，就可以加
修改代码（加入判断条件，修改函数的参数）：根据上面的想法以及判断条件，将递归的参数level和max去掉，改成left、right和n（都是括号个数），这里n就是输入，left和right都不能超过n
- Terminator: left == n and right == n，说明格子都用完了
- Drill down，if left < n，才能递归新的左括号；if left > right (and right <= n这条其实可以推出来，所以不用些)，才能递归新的右括号。递归的参数列表也都变成left、right
此时输出的结果都是合法的，虽然复杂度还是O(2^n)，但是通过判断条件，提前去掉了不合法的结果，减少了无用功。
之后还是看看题解，再看看国际版的。
人脑喜欢暴力递归，不喜欢寻找重复性。寻找到重复性，这个问题可以抽象为：什么时候生成左括号，什么时候生成右括号，以及最后输出。
养成做题后，阅读他人（国际站上）代码的习惯！！！有好的代码记下来，去模仿去学