高等数学第6章 向量代数与空间解析几何

高等数学第6章

什么是向量？

第一次接触向量应该是初中学习力的时候，力的三要素为：大小、方向、作用点，这三个要素也完全确定了一个向量（高等数学中考虑自由向量，即无作用点的区分）。我一直将向量看作一个带有箭头的线段，这是形象的，向量的加减运算是将一个向量的末端移动至另一个的首端进行三角形法则或平行四边形法则运算，这是向量运算最基础也是最本质的性质，与标量的数值运算不同。
向量的数量积是及其重要的概念：\(\vec{a}\cdot\vec{b}=|a|\cdot|b|\cdot{cos\theta}\)。第一次遇见仍然是在学习力学时，力做的功是力（作为一个向量）在沿位移方向的分量同位移大小的乘积，另外一个帮助理解的例子是高数课本上的：
液体流过平面\(S\)上面积为\(A\)的一个区域，液体在这区域上各点的流速均为\(\vec{v}\)。设\(\vec{n}\)是垂直于\(S\)的单位向量，计算单位时间内经过这区域流向\(\vec{n}\)所指一侧的液体的质量\(m\)(液体的密度为\(\rho\))

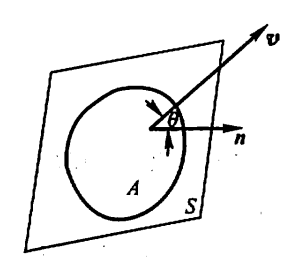
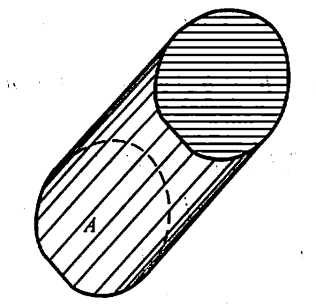
解：单位时间内流过该区域的液体组成一个底面积为\(A\)、斜高为\(|\vec{v}|\)的斜柱体，此斜柱体的高可知是\(|\vec{v}|\cdot{cos\theta}\)（\(\theta\)为\(\vec{v}\)与法向量\(\vec{n}\)的夹角）,因此体积为

\(A\cdot|\vec{v}|\cdot{cos\theta}=A\cdot\vec{v}\cdot\vec{n}\)
\(m=A\cdot\vec{v}\cdot\vec{n}\cdot\rho\)
向量的向量积也同样重要，若\(\vec{c}=\vec{a}\times\vec{b}\),则\(|\vec{c}|=|\vec{a}|\cdot|\vec{b}|\cdot{sin\theta}\)，\(\vec{c}\)的方向按右手定则从\(\vec{a}\)转向\(\vec{b}\).理解向量积是在学习杠杆知识后，施加在杠杆末端的力只有沿切向的分量才有实际作用，因此是\(|\vec{a}|\cdot|\vec{b}|\cdot{sin\theta}\)

曲面方程

1.曲面与方程

如果曲面\(S\)与方程\(F(x,y,z)=0\)有如下关系：

• 曲面\(S\)上任一点的坐标都满足方程\(F(x,y,z)=0\);
• 不在曲面\(S\)上的点的坐标都不满足方程\(F(x,y,x)=0\);

该如何理解呢？第一个条件说明了方程解\((x,y,z)\)的集合包含曲面上所有的点，第二个条件说明不在曲面上的点就不是方程的解，也就排除了方程解的集合中存在不在曲面上的情况。由此说明曲面与方程的对应关系。另外有一种特殊情况：\(z=f(x,y)\)，表示每一确定的\((x,y)\)对应一个\(z\)，此时的曲面是一个“单层的”，例如：\(z=\sqrt{x^2+y^2}\)，与此相对的例子是\(x^2+y^2+z^2=R^2\)，也就是\(z=\pm\sqrt{R^2-(x^2+y^2)}\)，此时一个\((x,y)\)对应两个\(z\)，曲面是“双层的”。

2.旋转曲面

以一条平面曲线绕其平面上的一条直线旋转一周所成的曲面。设在\(yOz\)平面有一已知曲线\(C\)，\(f(y,z)=0\)，当曲线\(C\)绕着\(z\)轴旋转时，点\(M_1(0,x_1,z_1)\)作为曲线\(C\)上的点，得到的另一点\(M(x,y,z)\),其中\(z=z_1\)保持不变，由旋转的性质可知，点\(M\)到\(z\)轴的距离与点\(M_1\)到\(z\)轴的距离相等，\(d=\sqrt{x^2+y^2}=|y_1|\)，由此将\(z_1=z,y_1=\pm\sqrt{x^2+y^2}\)代入\(f(y_1,z_1)=0\)，得到\(f(\pm\sqrt{x^2+y^2},z)=0\)，这样就得到了曲线旋转得到的曲面方程。

3.柱面

如\(x^2+y^2=R^2\)在三维坐标系中即为一个柱面方程，柱面是由直线沿着特定曲线\(C\)平行移动形成的轨迹。

空间曲线及其方程

空间曲线可以看作是两个曲面的交线，若曲面的方程为\(F(x,y,z)=0\)和\(G(x,y,z)=0\),则曲线的方程为：

\[\begin{cases} F(x,y,z)=0\\ G(x,y,z)=0 \end{cases}\]

空间曲线还可以用参数方程表示：

\[\begin{cases} x=x(t),\\ y=y(t),\\ z=z(t).\\ \end{cases}\]

一个常见的例子是螺旋线：

\[\begin{cases} x=acos(\omega{t}),\\ y=acos(\omega{t}),\\ z=vt.\\ \end{cases}\]

平面及其方程

平面的点法式方程是最直观的一种表示。因为过空间一点只能作唯一确定的平面垂直于一已知直线，因此，如果已知平面上一点\(M_0(x_0,y_0,z_0)\)和平面的一个法向量\(\vec{n}=(A,B,C)\)，则平面就完全确定的，平面上任一点\(M(x,y,z)\)与\(M_0\)组成的向量\(\vec{MM_0}\)与法向量\(\vec{n}\)垂直。因此：
\(\vec{n}\cdot\vec{MM_0}\)=0，\(A(x-x_0)+B(y-y_0)+C(z-z_0)=0\)
由点法式化简可得到平面的一般方程：
\(Ax+By+Cz+D=0\)

空间直线及其方程

• 作为空间曲线可以看作是两个曲面的交线的特例，空间直线可看作是两个平面的交线，若两个平面的方程为\(A_1x+B_1y+C_1z+D_1=0和A_2x+B_2y+C_2z+D_1=0\)，则空间直线可用如下方程组(此方程组是空间直线的一般方程)表示：

\[\begin{cases} A_1x+B_1y+C_1z+D_1=0\\ A_2x+B_2y+C_2z+D_2=0 \end{cases}\]

• 空间直线还有另外一种基于定义理解的表示方法（点向式方程）：若\(M_0(x_0,y_0,z_0)\)是空间直线上一确定点，并且已知空间直线的方向向量\(\vec{s}\)，那么此直线唯一确定。可知，直线上任一点\(M(x,y,z)\)与\(M_0(x_0,y_0,z_0)\)构成的向量\(\vec{MM_0}\)与方向向量\(\vec{s}\)平行，因此两向量的对应坐标成比例，故：

\[\frac{x-x_0}m=\frac{y-y_0}n=\frac{z-z_0}p \]

• 两空间直线的夹角
  两空间直线方向向量的夹角（通常指锐角）叫做两直线的夹角：

\[cos\varphi=\frac{|m_1m_2+n_1n_2+p_1p_2|}{\sqrt{m_1^2+n_1^2+p_1^2}\cdot\sqrt{m_2^2+n_2^2+p_2^2}} \]