LibreOJ 数列分块入门 1-9
数列分块入门1-9
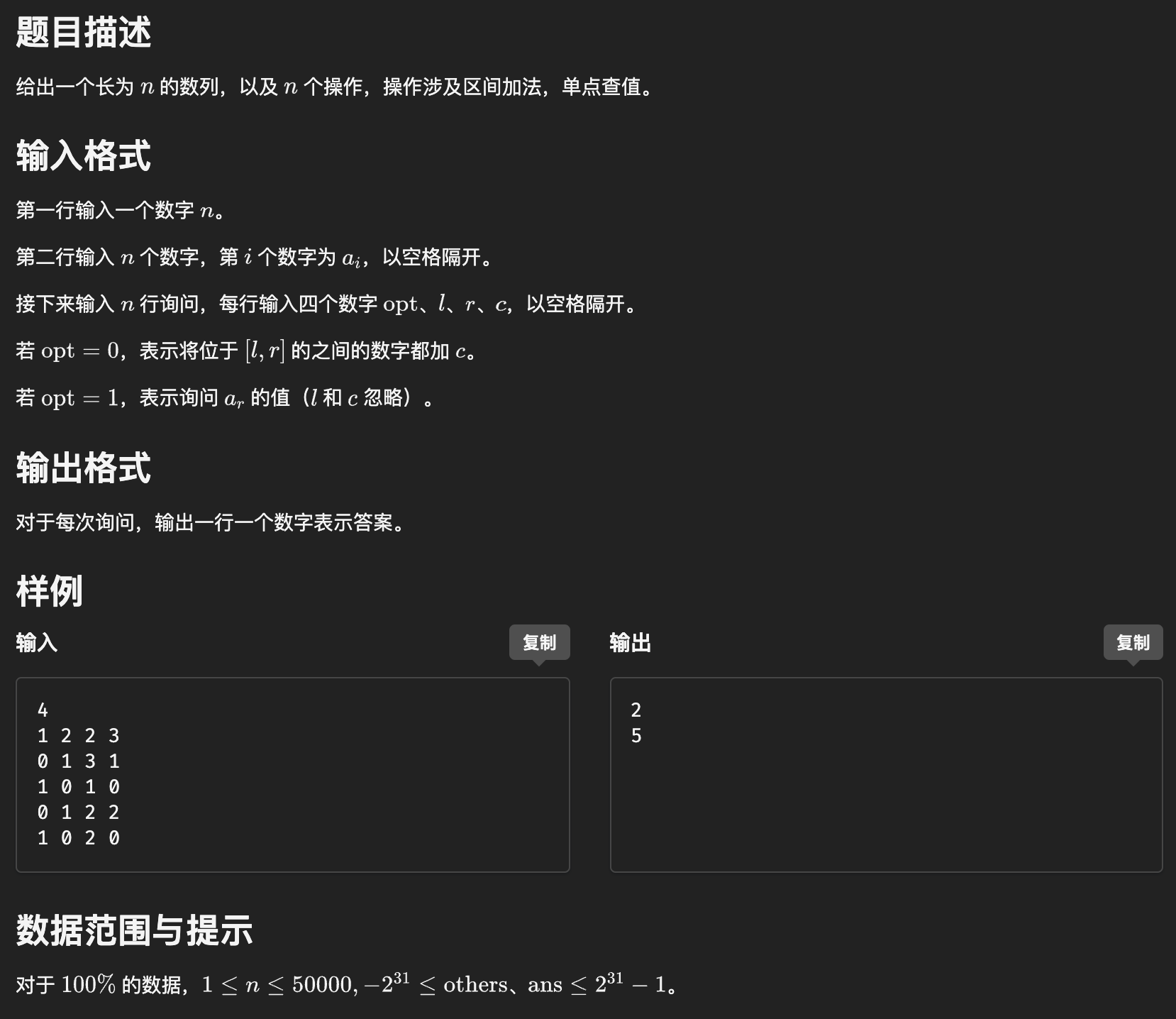
1. #6277. 数列分块入门 1
-
分析:分块基本操作,对于整块直接打上标记,询问的时候加上对应块的标记值即可.
-
代码:
#include <bits/stdc++.h>
#define ll long long
#define fi first
#define se second
#define pb push_back
#define me memset
#define rep(a,b,c) for(int a=b;a<=c;++a)
#define per(a,b,c) for(int a=b;a>=c;--a)
const int N = 1e6 + 10;
const int mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
using namespace std;
typedef pair<int,int> PII;
typedef pair<ll,ll> PLL;
ll gcd(ll a,ll b) {return b?gcd(b,a%b):a;}
ll lcm(ll a,ll b) {return a/gcd(a,b)*b;}
int n;
ll a[N],tag[N];
ll id[N];
void add(int l,int r,ll c){
int sid=id[l],eid=id[r];
if(sid==eid){
for(int i=l;i<=r;++i){
a[i]+=c;
}
return;
}
for(int i=l;sid==id[i];++i) a[i]+=c;
for(int i=sid+1;i<eid;++i) tag[i]+=c;
for(int i=r;eid==id[i];--i) a[i]+=c;
}
int main() {
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin>>n;
int len=sqrt(n);
for(int i=1;i<=n;++i){
id[i]=(i-1)/len+1;
cin>>a[i];
}
for(int i=1;i<=n;++i){
int op,l,r;
ll c;
cin>>op>>l>>r>>c;
if(op==0){
add(l,r,c);
}
else{
cout<<a[r]+tag[id[r]]<<'\n';
}
}
return 0;
}
2. #6278. 数列分块入门 2

-
分析:用二维数组将每个块内的元素都存起来,修改时,将整块外的元素修改完后,重新将这个块排序(二维数组),那么每次询问时,整块外的元素直接暴力算,整块的话用二分来求元素个数即可.
-
代码:
#include <bits/stdc++.h>
#define ll long long
#define fi first
#define se second
#define pb push_back
#define me memset
#define rep(a,b,c) for(int a=b;a<=c;++a)
#define per(a,b,c) for(int a=b;a>=c;--a)
const int N = 1e6 + 10;
const int mod = 1e9 + 7;
const int INF = 0x3f3f3f3f;
using namespace std;
typedef pair<int,int> PII;
typedef pair<ll,ll> PLL;
ll gcd(ll a,ll b) {return b?gcd(b,a%b):a;}
ll lcm(ll a,ll b) {return a/gcd(a,b)*b;}
int n;
ll a[N];
ll tag[N];
int id[N];
vector<ll> v[N];
int len;
void resort(int x){
v[x].clear();
for(int i=(x-1)*len+1;i<=min(x*len,n);++i){
v[x].pb(a[i]);
}
sort(v[x].begin(),v[x].end());
}
void add(int l,int r,ll c){
int sid=id[l],eid=id[r];
if(sid==eid){
for(int i=l;i<=r;++i){
a[i]+=c;
}
resort(id[l]);
return;
}
for(int i=l;sid==id[i];++i) a[i]+=c;
resort(sid);
for(int i=sid+1;i<eid;++i) tag[i]+=c;
for(int i=r;eid==id[i];--i) a[i]+=c;
resort(eid);
}
ll query(int l,int r,ll c){
int sid=id[l],eid=id[r];
ll ans=0;
if(sid==eid){
for(int i=l;i<=r;++i){
if(a[i]+tag[id[i]]<c) ans++;
}
return ans;
}
for(int i=l;sid==id[i];++i){
if(a[i]+tag[sid]<c) ans++;
}
for(int i=sid+1;i<eid;++i){
int cur=lower_bound(v[i].begin(),v[i].end(),c-tag[i])-v[i].begin();
ans+=cur;
}
for(int i=r;eid==id[i];--i){
if(a[i]+tag[eid]<c) ans++;
}
return ans;
}
int main() {
ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
cin>>n;
len=sqrt(n);
for(int i=1;i<=n;++i){
cin>>a[i];
id[i]=(i-1)/len+1;
v[id[i]].pb(a[i]);
}
for(int i=1;i<=id[n];++i){
sort(v[i].begin(),v[i].end());
}
for(int i=1;i<=n;++i){
int op,l,r;
ll c;
cin>>op>>l>>r>>c;
if(op==0){
add(l,r,c);
}
else cout<<query(l,r,c*c)<<'\n';
}
return 0;
}
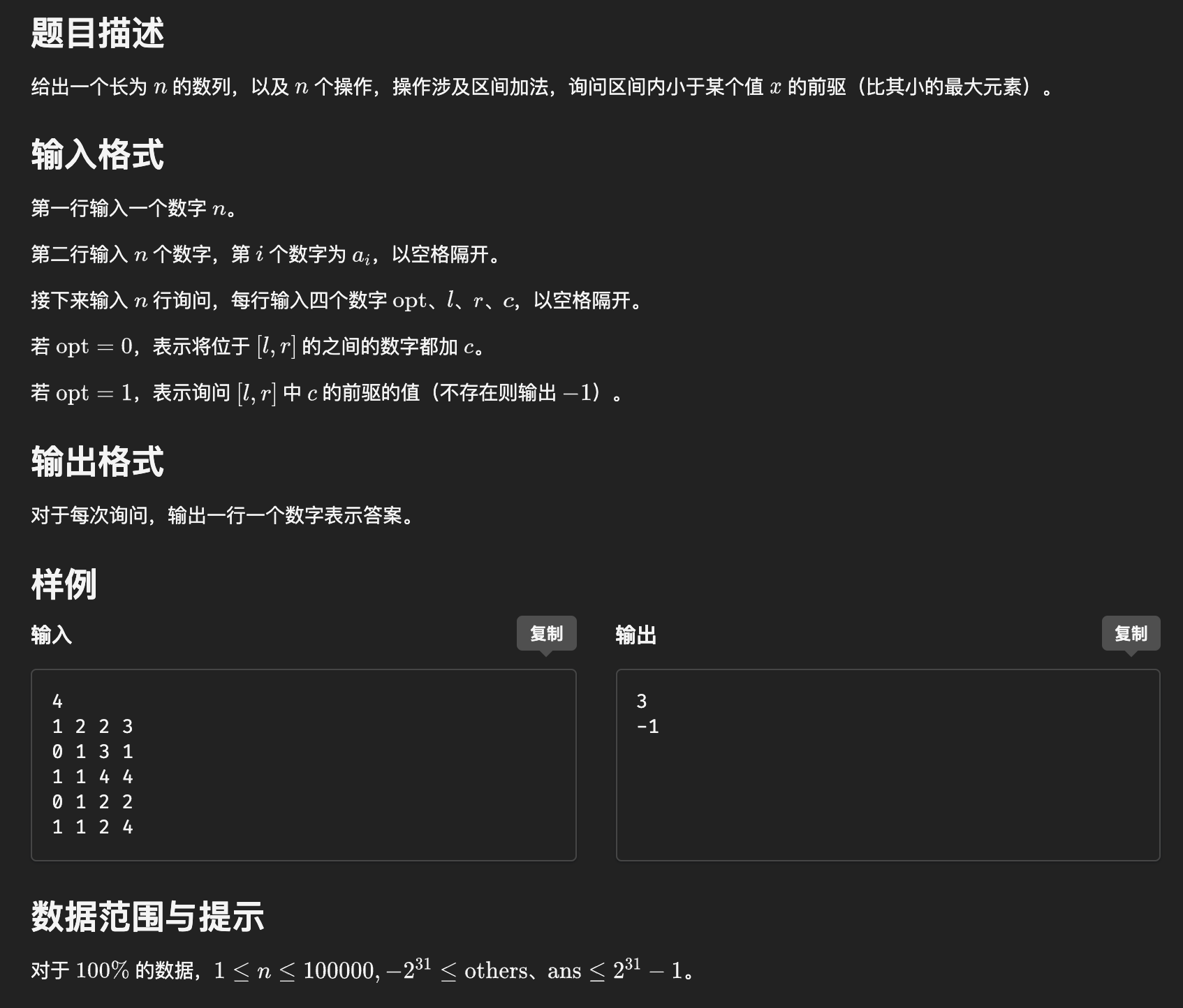
3. #6279. 数列分块入门 3
-
分析:与2一样,用二维数组存每个块内的元素,整块外的暴力算,整块内的用二分求即可.
-
代码:
#include <bits/stdc++.h> #define ll long long #define fi first #define se second #define pb push_back #define me memset #define rep(a,b,c) for(int a=b;a<=c;++a) #define per(a,b,c) for(int a=b;a>=c;--a) const int N = 1e6 + 10; const int mod = 1e9 + 7; const int INF = 0x3f3f3f3f; using namespace std; typedef pair<int,int> PII; typedef pair<ll,ll> PLL; ll gcd(ll a,ll b) {return b?gcd(b,a%b):a;} ll lcm(ll a,ll b) {return a/gcd(a,b)*b;} int n; ll a[N]; ll tag[N]; int id[N]; vector<ll> v[N]; int len; void resort(int x){ v[x].clear(); for(int i=(x-1)*len+1;i<=min(x*len,n);++i){ v[x].pb(a[i]); } sort(v[x].begin(),v[x].end()); } void add(int l,int r,ll c){ int sid=id[l],eid=id[r]; if(sid==eid){ for(int i=l;i<=r;++i){ a[i]+=c; } resort(sid); return; } for(int i=l;sid==id[i];++i) a[i]+=c; resort(sid); for(int i=sid+1;i<eid;++i) tag[i]+=c; for(int i=r;eid==id[i];--i) a[i]+=c; resort(eid); } ll query(int l,int r,ll c){ int sid=id[l],eid=id[r]; ll ans=-1; if(sid==eid){ for(int i=l;i<=r;++i){ if(a[i]+tag[sid]<c){ ans=max(ans,a[i]+tag[sid]); } } return ans; } for(int i=l;sid==id[i];++i){ if(a[i]+tag[sid]<c){ ans=max(ans,a[i]+tag[sid]); } } for(int i=sid+1;i<eid;++i){ auto it=lower_bound(v[i].begin(),v[i].end(),c-tag[i]); if(it==v[i].begin()) continue; ll x=*(--it); if(x+tag[i]<c){ ans=max(ans,x+tag[i]); } } for(int i=r;eid==id[i];--i){ if(a[i]+tag[eid]<c){ ans=max(ans,a[i]+tag[eid]); } } return ans; } int main() { ios::sync_with_stdio(false);cin.tie(0);cout.tie(0); cin>>n; len=sqrt(n); for(int i=1;i<=n;++i){ cin>>a[i]; id[i]=(i-1)/len+1; v[id[i]].pb(a[i]); } for(int i=1;i<=n;++i){ sort(v[i].begin(),v[i].end()); } for(int i=1;i<=n;++i){ int op,l,r; ll c; cin>>op>>l>>r>>c; if(op==0){ add(l,r,c); } else cout<<query(l,r,c)<<'\n'; } return 0; }
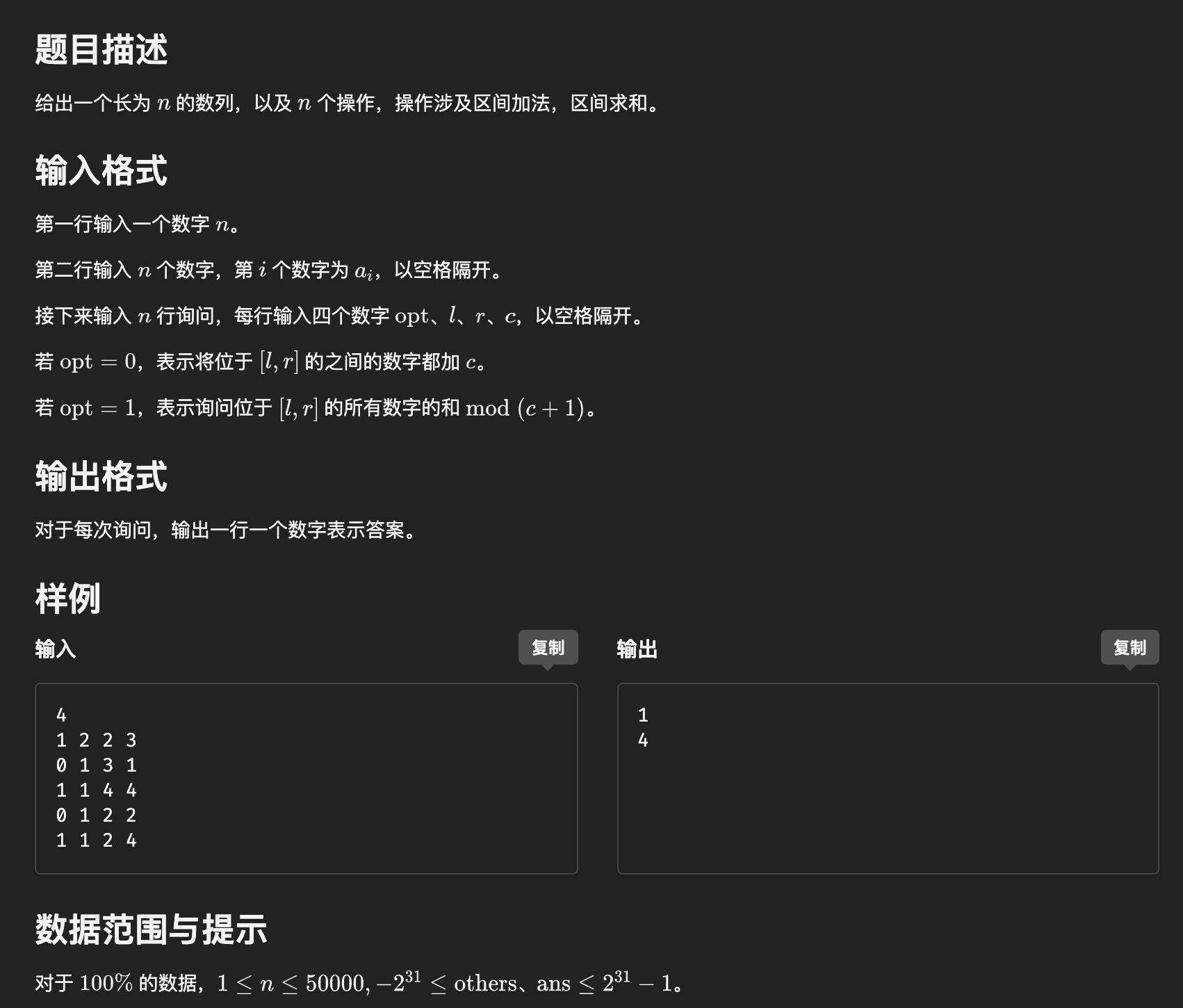
4. #6280. 数列分块入门 4
-
分析:分块基本操作,对整块打标记,询问时加上对应块的标记值即可.
-
代码:
#include <bits/stdc++.h> #define ll long long #define fi first #define se second #define pb push_back #define me memset #define rep(a,b,c) for(int a=b;a<=c;++a) #define per(a,b,c) for(int a=b;a>=c;--a) const int N = 1e6 + 10; const int mod = 1e9 + 7; const int INF = 0x3f3f3f3f; using namespace std; typedef pair<int,int> PII; typedef pair<ll,ll> PLL; ll gcd(ll a,ll b) {return b?gcd(b,a%b):a;} ll lcm(ll a,ll b) {return a/gcd(a,b)*b;} int n; ll a[N]; int id[N]; ll tag[N]; ll s[N]; int len; void add(int l,int r,ll c){ int sid=id[l],eid=id[r]; if(sid==eid){ for(int i=l;i<=r;++i){ a[i]+=c; s[sid]+=c; } return; } for(int i=l;sid==id[i];++i) a[i]+=c,s[sid]+=c; for(int i=sid+1;i<eid;++i) tag[i]+=c,s[i]+=len*c; for(int i=r;eid==id[i];--i) a[i]+=c,s[eid]+=c; } ll query(int l,int r,ll c){ int sid=id[l],eid=id[r]; ll ans=0; if(sid==eid){ for(int i=l;i<=r;++i){ ans=(ans+a[i]+tag[sid])%c; } return ans; } for(int i=l;sid==id[i];++i) ans=(ans+a[i]+tag[sid])%c; for(int i=sid+1;i<eid;++i) ans=(ans+s[i])%c; for(int i=r;eid==id[i];--i) ans=(ans+a[i]+tag[eid])%c; return ans; } int main() { ios::sync_with_stdio(false);cin.tie(0);cout.tie(0); cin>>n; len=sqrt(n); for(int i=1;i<=n;++i){ cin>>a[i]; id[i]=(i-1)/len+1; s[id[i]]+=a[i]; } for(int i=1;i<=n;++i){ int op,l,r; ll c; cin>>op>>l>>r>>c; if(op==0){ add(l,r,c); } else cout<<query(l,r,c+1)<<'\n'; } return 0; }
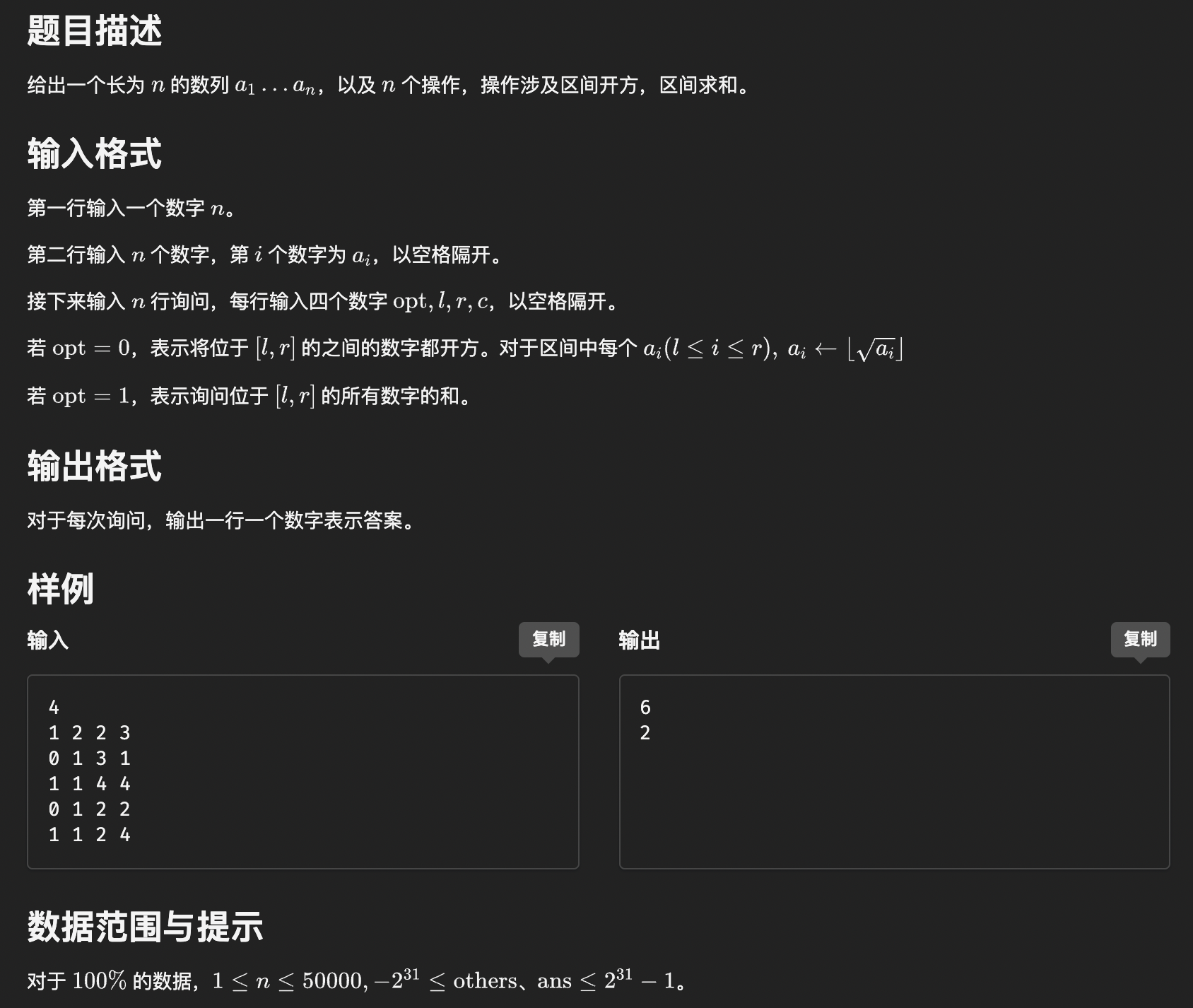
5. #6281. 数列分块入门 5
-
分析:根据数据范围,发现一个数最多连续开方\(5\)次后就会变成\(1\).有了这个性质,我们只要判断整块是否全是\(1\)就可以极大的降低复杂度.要注意\(a_i\)可能为\(0\)的情况.具体实现就可以每次操作前判断要操作的块是否已经全是\(<=1\),如果是就不操作,如果不是就暴力求一下,然后再判断即可.
-
代码:
#include <bits/stdc++.h> #define ll long long #define fi first #define se second #define pb push_back #define me memset #define rep(a,b,c) for(int a=b;a<=c;++a) #define per(a,b,c) for(int a=b;a>=c;--a) const int N = 1e6 + 10; const int mod = 1e9 + 7; const int INF = 0x3f3f3f3f; using namespace std; typedef pair<int,int> PII; typedef pair<ll,ll> PLL; ll gcd(ll a,ll b) {return b?gcd(b,a%b):a;} ll lcm(ll a,ll b) {return a/gcd(a,b)*b;} int n; ll a[N]; ll s[N]; int id[N]; int len; bool vis[N]; void rejudge(int x){ bool flag=false; for(int i=(x-1)*len+1;i<=min(x*len,n);++i){ if(a[i]>1) flag=true; } if(!flag) vis[x]=false; } void square(int l,int r){ int sid=id[l],eid=id[r]; if(sid==eid){ if(!vis[sid]) return; for(int i=l;i<=r;++i){ s[sid]-=a[i]; a[i]=sqrt(a[i]); s[sid]+=a[i]; } rejudge(sid); return; } if(vis[sid]){ for(int i=l;id[i]==sid;++i){ s[sid]-=a[i]; a[i]=sqrt(a[i]); s[sid]+=a[i]; } rejudge(sid); } for(int i=sid+1;i<eid;++i){ if(!vis[i]) continue; for(int j=(i-1)*len+1;j<=i*len;++j){ s[i]-=a[j]; a[j]=sqrt(a[j]); s[i]+=a[j]; } rejudge(i); } if(vis[eid]){ for(int i=r;id[i]==eid;--i){ s[eid]-=a[i]; a[i]=sqrt(a[i]); s[eid]+=a[i]; } rejudge(eid); } } ll query(int l,int r){ int sid=id[l],eid=id[r]; ll ans=0; if(sid==eid){ for(int i=l;i<=r;++i){ ans+=a[i]; } return ans; } for(int i=l;id[i]==sid;++i) ans+=a[i]; for(int i=sid+1;i<eid;++i) ans+=s[i]; for(int i=r;id[i]==eid;--i) ans+=a[i]; return ans; } int main() { ios::sync_with_stdio(false);cin.tie(0);cout.tie(0); //freopen("/Users/somnus/Desktop/data/in.txt","r",stdin); cin>>n; len=sqrt(n); for(int i=1;i<=n;++i){ cin>>a[i]; id[i]=(i-1)/len+1; if(a[i]!=0 && a[i]!=1) vis[id[i]]=true; s[id[i]]+=a[i]; } for(int i=1;i<=n;++i){ int op,l,r; ll c; cin>>op>>l>>r>>c; if(op==0){ square(l,r); } else cout<<query(l,r)<<'\n'; } return 0; }
6. #6282. 数列分块入门 6

-
分析:用二维数组存每个块内的元素,每次操作都是暴力insert插入,但是当某个块的内的元素很多时,复杂度会很大,此时我们对块长\(block\)重构即可,询问时先判断询问位置在哪个块内,然后直接输出.复杂度\(O(n*\sqrt n)\).
-
代码:
#include <bits/stdc++.h> #define ll long long #define fi first #define se second #define pb push_back #define me memset #define rep(a,b,c) for(int a=b;a<=c;++a) #define per(a,b,c) for(int a=b;a>=c;--a) const int N = 1e6 + 10; const int mod = 1e9 + 7; const int INF = 0x3f3f3f3f; using namespace std; typedef pair<int,int> PII; typedef pair<ll,ll> PLL; ll gcd(ll a,ll b) {return b?gcd(b,a%b):a;} ll lcm(ll a,ll b) {return a/gcd(a,b)*b;} int n; int a[N]; vector<int> v[N]; int len,block; PII find(int u){ int i=1; while(u>(int)v[i].size()){ u-=(int)v[i].size(); i++; } return make_pair(u,i); } void resize(){ vector<int> tmp; for(int i=1;i<=block;++i){ for(auto w:v[i]){ tmp.pb(w); } v[i].clear(); } len=sqrt((int)tmp.size()); block=((int)tmp.size()-1)/len+1; for(int i=0;i<(int)tmp.size();++i){ int cur=i+1; v[(cur-1)/len+1].pb(tmp[i]); } } void insert(int u,int k){ PII p=find(u); v[p.se].insert(v[p.se].begin()+p.fi-1,k); if((int)v[p.se].size()>20*len) resize(); } int main() { ios::sync_with_stdio(false);cin.tie(0);cout.tie(0); cin>>n; len=sqrt(n); block=(n-1)/len+1; for(int i=1;i<=n;++i){ cin>>a[i]; v[(i-1)/len+1].pb(a[i]); } for(int i=1;i<=n;++i){ int op,l,r; ll c; cin>>op>>l>>r>>c; if(op==0){ insert(l,r); } else{ PII res=find(r); cout<<v[res.se][res.fi-1]<<'\n'; } } return 0; }
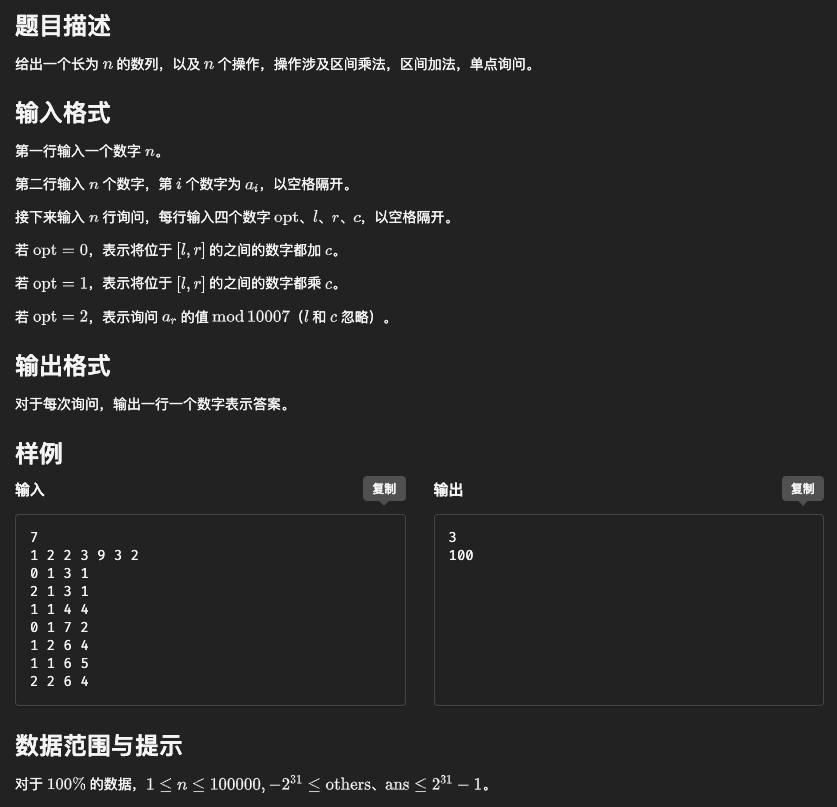
7. #6283. 数列分块入门 7
-
分析:对于整块分别对加法和乘法打标记,注意乘法标记的时候要算同时更新加法的标记.
-
代码:
#include <bits/stdc++.h> #define ll long long #define fi first #define se second #define pb push_back #define me memset #define rep(a,b,c) for(int a=b;a<=c;++a) #define per(a,b,c) for(int a=b;a>=c;--a) const int N = 1e6 + 10; const int mod = 10007; const int INF = 0x3f3f3f3f; using namespace std; typedef pair<int,int> PII; typedef pair<ll,ll> PLL; ll gcd(ll a,ll b) {return b?gcd(b,a%b):a;} ll lcm(ll a,ll b) {return a/gcd(a,b)*b;} int n; ll a[N]; int id[N]; int len,block; ll tag_mul[N],tag_add[N]; void pushtag(int x){ for(int i=(x-1)*len+1;i<=min(n,x*len);++i){ a[i]=(a[i]*tag_mul[x]+tag_add[x])%mod; } tag_mul[x]=1; tag_add[x]=0; } void update(int l,int r,ll c,int op){ int sid=id[l],eid=id[r]; if(sid==eid){ pushtag(sid); for(int i=l;i<=r;++i){ if(op==0){ a[i]=(a[i]+c)%mod; } else{ a[i]=a[i]*c%mod; } } return; } pushtag(sid); for(int i=l;id[i]==sid;++i){ if(op==0){ a[i]=(a[i]+c)%mod; } else a[i]=a[i]*c%mod; } for(int i=sid+1;i<eid;++i){ if(op==0){ tag_add[i]=(tag_add[i]+c)%mod; } else{ tag_add[i]=(tag_add[i]*c)%mod; tag_mul[i]=(tag_mul[i]*c)%mod; } } pushtag(eid); for(int i=r;id[i]==eid;--i){ if(op==0){ a[i]=(a[i]+c)%mod; } else a[i]=a[i]*c%mod; } } ll query(int x){ return (a[x]*tag_mul[id[x]]%mod+tag_add[id[x]])%mod; } int main() { ios::sync_with_stdio(false);cin.tie(0);cout.tie(0); cin>>n; len=sqrt(n); block=(n-1)/len+1; for(int i=1;i<=n;++i){ cin>>a[i]; id[i]=(i-1)/len+1; tag_mul[id[i]]=1; } for(int i=1;i<=n;++i){ int op,l,r; ll c; cin>>op>>l>>r>>c; if(op==0 || op==1){ update(l,r,c,op); } else cout<<query(r)<<'\n'; } return 0; }
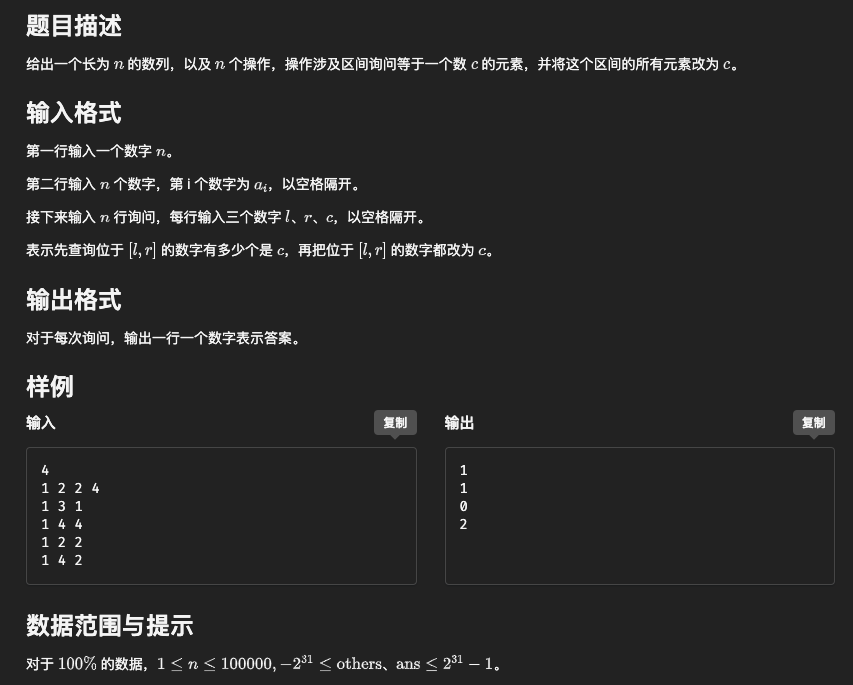
8.#6284. 数列分块入门 8
-
分析:和之前的sqrt一样,操作一定次数之后,某些整块内的元素都相同, 可以对整块标记,每次对于整块外的元素操作时,先把标记push给所在的块,对于整块操作时,如果当前块有标记,判断标记值是否为\(c\),如果是,直接贡献块长给答案,如果不是,直接修改标记值,如果当前块没有标记,暴力统计贡献给答案,然后打上标记.
-
代码:
#include <bits/stdc++.h> #define ll long long #define fi first #define se second #define pb push_back #define me memset #define rep(a,b,c) for(int a=b;a<=c;++a) #define per(a,b,c) for(int a=b;a>=c;--a) const int N = 1e6 + 10; const int mod = 1e9 + 7; const int INF = 0x3f3f3f3f; using namespace std; typedef pair<int,int> PII; typedef pair<ll,ll> PLL; ll gcd(ll a,ll b) {return b?gcd(b,a%b):a;} ll lcm(ll a,ll b) {return a/gcd(a,b)*b;} int n; ll a[N]; int id[N]; ll tag[N]; int len; void pushtag(int x){ if(tag[x]==-1) return; for(int i=(x-1)*len+1;i<=min(n,x*len);++i){ a[i]=tag[x]; } tag[x]=-1; } ll query(int l,int r,ll c){ int sid=id[l],eid=id[r]; ll ans=0; if(sid==eid){ pushtag(sid); for(int i=l;i<=r;++i){ if(a[i]==c) ans++; else a[i]=c; } return ans; } pushtag(sid); for(int i=l;id[i]==sid;++i){ if(a[i]==c) ans++; else a[i]=c; } for(int i=sid+1;i<eid;++i){ if(tag[i]!=-1){ if(tag[i]==c) ans+=len; else tag[i]=c; } else{ for(int j=(i-1)*len+1;j<=i*len;++j){ if(a[j]==c) ans++; } tag[i]=c; } } pushtag(eid); for(int i=r;id[i]==eid;--i){ if(a[i]==c) ans++; else a[i]=c; } return ans; } int main() { ios::sync_with_stdio(false);cin.tie(0);cout.tie(0); cin>>n; len=sqrt(n); me(tag,-1,sizeof(tag)); for(int i=1;i<=n;++i){ cin>>a[i]; id[i]=(i-1)/len+1; } for(int i=1;i<=n;++i){ int l,r; ll c; cin>>l>>r>>c; cout<<query(l,r,c)<<'\n'; } return 0; }
9.#6285. 数列分块入门 9

-
分析:离散化,用二维数组存记录每个数的位置,预处理维护每个块及其后面的位置的众数,这样询问的时候就可以\(O(1)\)得出所有整块的众数,然后对于非整块,可以枚举每个元素,利用之前存的位置,二分得出众数个数,再加上\(vis\)数组进行优化,注意块长不能取\(\sqrt n\),取\(150\)可以过.
-
代码:
#include <bits/stdc++.h> #define ll long long #define fi first #define se second #define pb push_back #define me memset #define rep(a,b,c) for(int a=b;a<=c;++a) #define per(a,b,c) for(int a=b;a>=c;--a) const int N = 1e5 + 10; const int mod = 1e9 + 7; const int INF = 0x3f3f3f3f; using namespace std; typedef pair<int,int> PII; typedef pair<ll,ll> PLL; ll gcd(ll a,ll b) {return b?gcd(b,a%b):a;} ll lcm(ll a,ll b) {return a/gcd(a,b)*b;} int n; int a[N]; int id[N]; int len,block; map<int,int> mp; int val[N]; vector<int> v[N]; int cnt[N]; int res[2050][2050]; bool vis[N]; void init(int x){ int mx_cnt=0,mx=0; me(cnt,0,sizeof(cnt)); for(int i=(x-1)*len+1;i<=n;++i){ cnt[a[i]]++; if(cnt[a[i]]>mx_cnt || (cnt[a[i]]==mx_cnt && val[a[i]]<val[mx])){ mx_cnt=cnt[a[i]]; mx=a[i]; } res[x][id[i]]=mx; } } int get_len(int l,int r,int val){ return upper_bound(v[val].begin(),v[val].end(),r)-lower_bound(v[val].begin(),v[val].end(),l); } int query(int l,int r){ int sid=id[l],eid=id[r]; int mx=res[sid+1][eid-1]; //整块的mx_ele int mx_cnt=get_len(l,r,mx); me(vis,false,sizeof(vis)); vis[mx]=true; if(sid==eid){ for(int i=l;i<=r;++i){ if(!vis[a[i]]){ vis[a[i]]=true; int cur=get_len(l,r,a[i]); if(cur>mx_cnt || (cur==mx_cnt && val[a[i]]<val[mx])){ mx_cnt=cur; mx=a[i]; } } } return val[mx]; } for(int i=l;id[i]==sid;++i){ if(!vis[a[i]]){ vis[a[i]]=true; int cur=get_len(l,r,a[i]); if(cur>mx_cnt || (cur==mx_cnt && val[a[i]]<val[mx])){ mx_cnt=cur; mx=a[i]; } } } for(int i=r;id[i]==eid;--i){ if(!vis[a[i]]){ vis[a[i]]=true; int cur=get_len(l,r,a[i]); if(cur>mx_cnt || (cur==mx_cnt && val[a[i]]<val[mx])){ mx_cnt=cur; mx=a[i]; } } } return val[mx]; } int main() { scanf("%d",&n); len=150; block=(n-1)/len+1; int idx=0; for(int i=1;i<=n;++i){ cin>>a[i]; id[i]=(i-1)/len+1; if(!mp[a[i]]){ mp[a[i]]=++idx; val[idx]=a[i]; } a[i]=mp[a[i]]; v[a[i]].pb(i); } for(int i=1;i<=block;++i){ init(i); } for(int i=1;i<=n;++i){ int l,r; scanf("%d %d",&l,&r); printf("%d\n",query(l,r)); } return 0; }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号