洛谷 P1429 平面最近点对(加强版) (分治模板题)
-
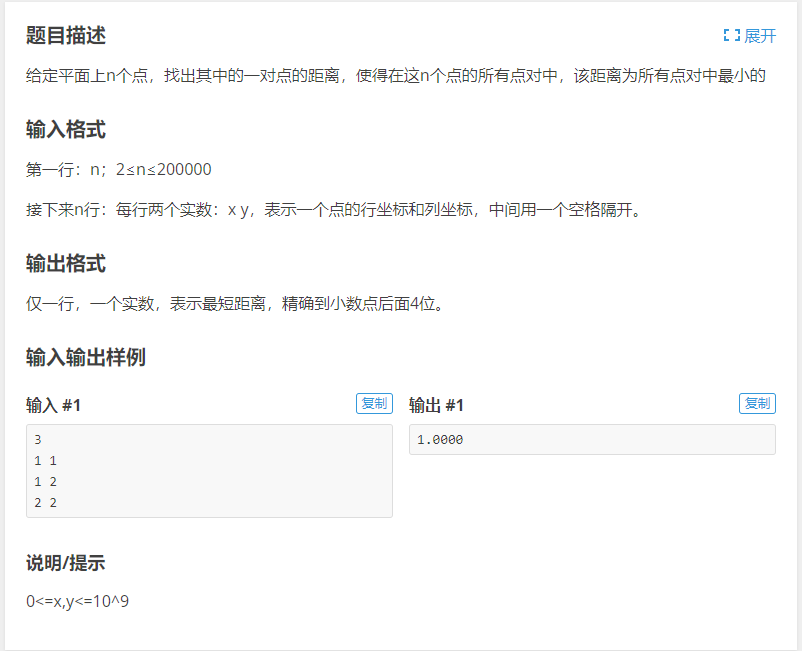
题意:有\(n\)个点对,找到它们之间的最短距离.
-
题解:我们先对所有点对以\(x\)的大小进行排序,然后分治,每次左右二等分递归下去,当\(l+1=r\)的时候,我们计算一下距离直接返回给上一层,若\(l==r\)说明只有一个点,不能构成线段,返回\(INF\),于是当前区间的左右两边的最短距离我们找到了,之后还有一种情况,就是一个点在\(mid\)左边,一个在\(mid\)右边,由于左右两边的最短距离\(d\)已知,所以我们可以再划分一个区间\([mid-d,mid+d]\),容易证明,若最短距离横穿\(mid\)线的话,两点一定在这个区间内,我们用\(tmp\)数组记录区间内的点,然后再枚举这些点求它们的距离,但是这里要优化一下,假如它们之间纵坐标的距离>\(d\),那么一定是不合法的,具体细节见代码.
-
代码:
struct misaka{ double x,y; }e[N],tmp[N]; int n; bool cmp1(misaka a,misaka b){ if(a.x==b.x) return a.y<b.y; return a.x<b.x; } bool cmp2(misaka a,misaka b){ if(a.y==b.y) return a.x<b.x; return a.y<b.y; } double dis(misaka a,misaka b){ //求距离 double res=fabs(a.x-b.x)*fabs(a.x-b.x)+fabs(a.y-b.y)*fabs(a.y-b.y); return sqrt(res); } double MIN(double a,double b){ //手写求min if(a>b) return b; else return a; } double merge(int l,int r){ if(l==r) return INF; //只有一个点 if(l+1==r) return dis(e[l],e[r]); //递归边界,直接返回给上一层 int mid=(l+r)>>1; int cnt=0; double d=MIN(merge(l,mid),merge(mid+1,r)); //求左边和右边的最小距离 for(int i=l;i<=r;++i){ if(fabs(e[mid].x-e[i].x)<=d){ //判断点是否在[mid-x,mid+x]内 tmp[++cnt]=e[i]; } } sort(tmp+1,tmp+1+cnt,cmp2); //按纵坐标排序 for(int i=1;i<=cnt;++i){ for(int j=i+1;j<=cnt && fabs(tmp[i].y-tmp[j].y)<=d;++j){ //若纵坐标的差大于d,直接下一个点 d=MIN(d,dis(tmp[i],tmp[j])); } } return d; } int main() { //ios::sync_with_stdio(false);cin.tie(0);cout.tie(0); scanf("%d",&n); for(int i=1;i<=n;++i) scanf("%lf %lf",&e[i].x,&e[i].y); sort(e+1,e+1+n,cmp1); double ans=merge(1,n); printf("%.4f\n",ans); return 0; }
𝓐𝓬𝓱𝓲𝓮𝓿𝓮𝓶𝓮𝓷𝓽 𝓹𝓻𝓸𝓿𝓲𝓭𝓮𝓼 𝓽𝓱𝓮 𝓸𝓷𝓵𝔂 𝓻𝓮𝓪𝓵
𝓹𝓵𝓮𝓪𝓼𝓾𝓻𝓮 𝓲𝓷 𝓵𝓲𝓯𝓮


 浙公网安备 33010602011771号
浙公网安备 33010602011771号