洛谷 P1077 摆花 (背包DP)
-
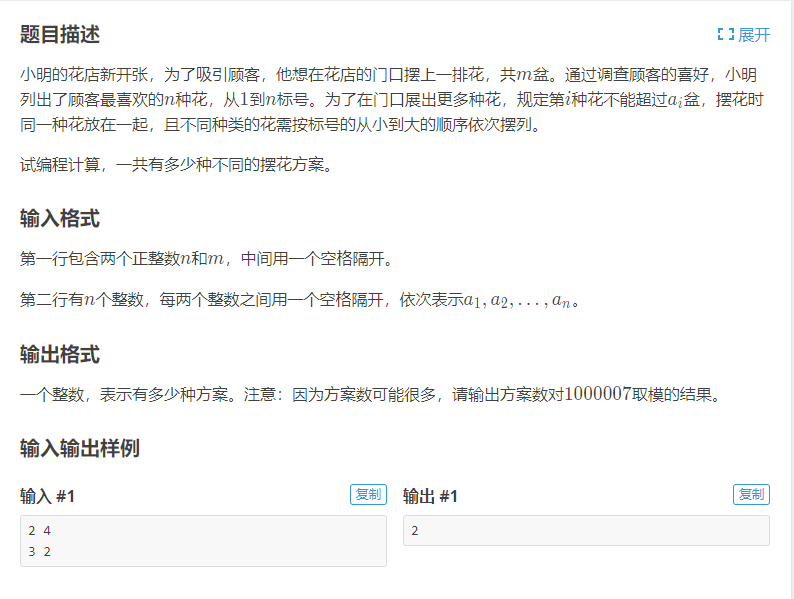
题意:有\(n\)种花,每种花有\(a_i\)盆,现在要摆\(m\)盆花,花的种类从\([1,n]\)有序排放,问有多少种方案数.
-
题解:这题可以借用01背包的思路,感觉更好想一点,我们首先枚举\(n\)种花,然后按一维01背包的思路,再枚举第\(i\)种花的选取盆数\([1,min(a_i,j)]\),每次状态都由\(dp[j-k]\)转化而来,有点难想的是边界问题,因为我们只能先放第一种花,第一个位置必须放第一种花,所以我们让\(dp[0]=1\),只有当一个位置放了第一盆花之后,后面的花的状态才能得到更新.
-
代码:
int n,m; int a[N]; int dp[N]; int main() { ios::sync_with_stdio(false);cin.tie(0);cout.tie(0); cin>>n>>m; for(int i=1;i<=n;++i){ cin>>a[i]; } dp[0]=1; for(int i=1;i<=n;++i){ for(int j=m;j>=1;--j){ for(int k=1;k<=min(a[i],j);++k){ dp[j]=(dp[j]+dp[j-k])%mod; //cout<<i<<" "<<" "<<j<<" "<<dp[j]<<endl; 这里便于理解状态之间的关系 } } } cout<<dp[m]<<endl; return 0; }
𝓐𝓬𝓱𝓲𝓮𝓿𝓮𝓶𝓮𝓷𝓽 𝓹𝓻𝓸𝓿𝓲𝓭𝓮𝓼 𝓽𝓱𝓮 𝓸𝓷𝓵𝔂 𝓻𝓮𝓪𝓵
𝓹𝓵𝓮𝓪𝓼𝓾𝓻𝓮 𝓲𝓷 𝓵𝓲𝓯𝓮


 浙公网安备 33010602011771号
浙公网安备 33010602011771号