AtCoder Beginner Contest 179 D - Leaping Tak (DP)

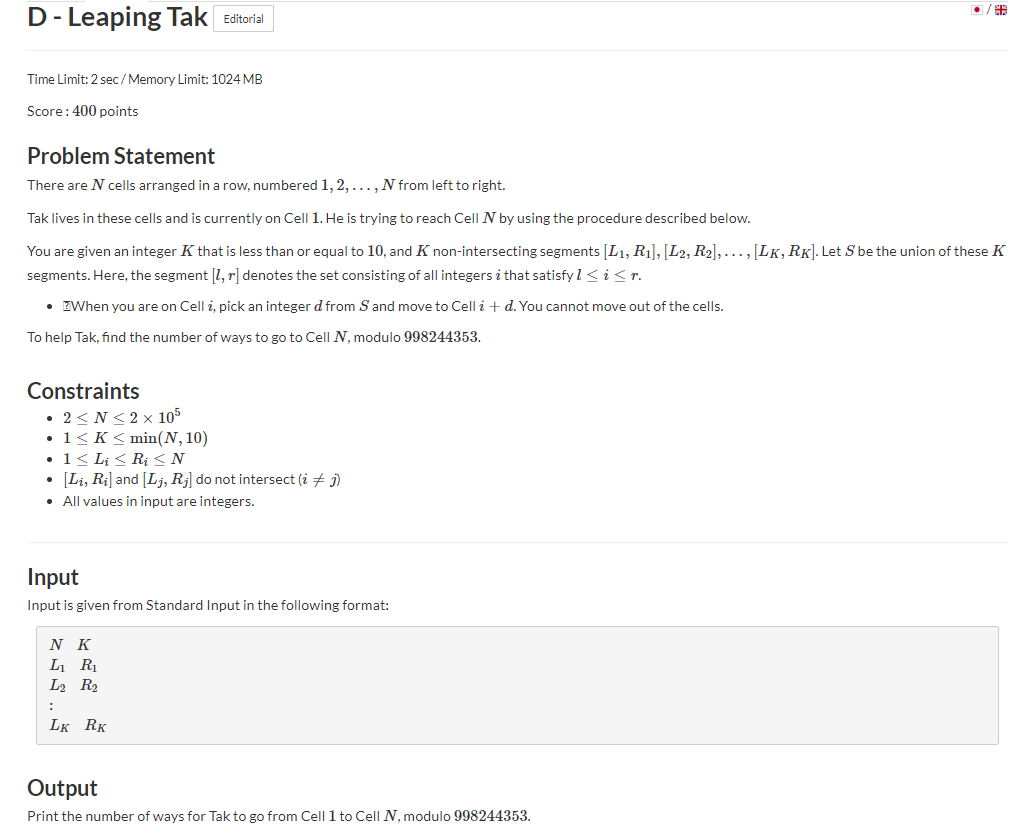
• 题意:给你一个数字\(n\)和\(k\)个区间,\(S\)表示所有区间的并的集合,你目前在\(1\),每次可以从集合中选择一个数字向右移动,问有多少种方法从\(1\)走到\(n\).

• 题解:我们从1开始遍历,\(dp[i]\)表示走到目前走到\(i\)的方案数,再去遍历每一个集合,用\(dp[i]\)更新所有\([i+l[j],i+r[j]]\)中的点,而遍历区间我们可以用差分来\(O(n)\)的运行出来.

• 代码:

  int n,k;
  int l[N],r[N];
  ll dp[N];
  
  
  int main() {
      ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
      cin>>n>>k;
      for(int i=1;i<=k;++i){
      	cin>>l[i]>>r[i];
      }
      dp[1]=1;
      dp[2]=-1;
      for(int i=1;i<=n;++i){
      	dp[i]+=dp[i-1];;
      	dp[i]=(dp[i]%mod+mod)%mod;
      	for(int j=1;j<=k;++j){
      		dp[i+l[j]]+=dp[i];
      		dp[i+r[j]+1]-=dp[i];
      	}
      }
      cout<<dp[n]<<endl;
      return 0;
  }