Atcoder Educational DP Contest I - Coins (概率DP)

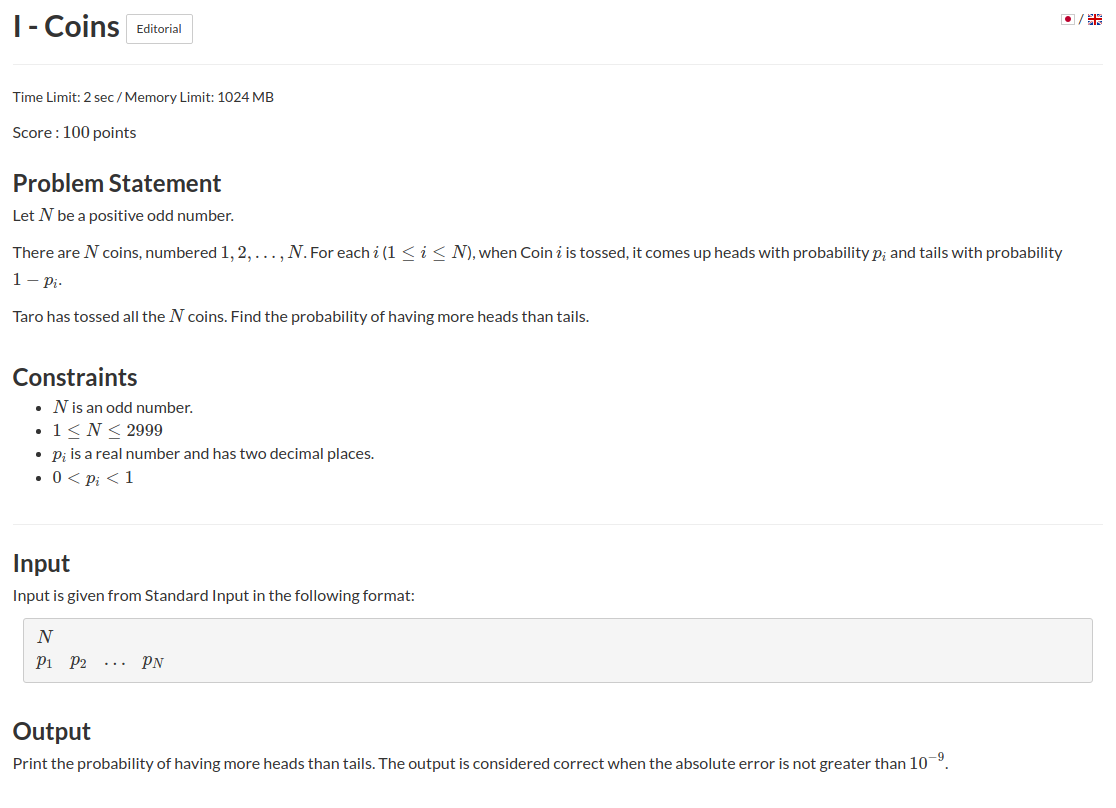
• 题意:有\(n\)枚硬币,每枚硬币抛完后向上的概率为\(p[i]\),现在求抛完后向上的硬币个数大于向下的概率.

• 题解:我们用二维的\(dp[i][j]\)来表示状态,\(i\)表示当前抛的是第\(i\)个硬币,\(j\)表示的是前\(i\)个硬币中向上的个数,那么状态可以表示为,如果\(j=0\),那么\(dp[i][j]=dp[i-1][j]*(1-p[i])\),否则,\(dp[i][j]=dp[i-1][j-1]*p[i]+dp[i-1][j]*(1-p[i])\).即类似01背包的思路,当前这个状态我选还是不选.如果选,那么因为是\(j\)个朝上,所以要由前一枚硬币有\(j-1\)个朝上的状态转化而来,反之同理.

• 代码:

  int n;
  double p[N];
  double dp[4000][4000];
  int main() {
      //ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
  	n=read();
  	for(int i=1;i<=n;++i){
  		scanf("%lf",&p[i]);
  	}
   
  	dp[1][0]=1-p[1];
  	dp[1][1]=p[1];
   
  	for(int i=2;i<=n;++i){
  		for(int j=0;j<=i;++j){
  			if(j==0){
  				dp[i][j]=dp[i-1][j]*(1-p[i]);
  			}
  			else{
  				dp[i][j]=dp[i-1][j-1]*p[i]+dp[i-1][j]*(1-p[i]);
  			}
  		}
  	}
  	double res=0.0000000000;
  	for(int i=(n/2)+1;i<=n;++i){
  		res+=dp[n][i];
  	}
  	printf("%.10lf",res);
   
      return 0;
  }