GYM101810 ACM International Collegiate Programming Contest, Amman Collegiate Programming Contest (2018) M. Greedy Pirate (LCA)
-
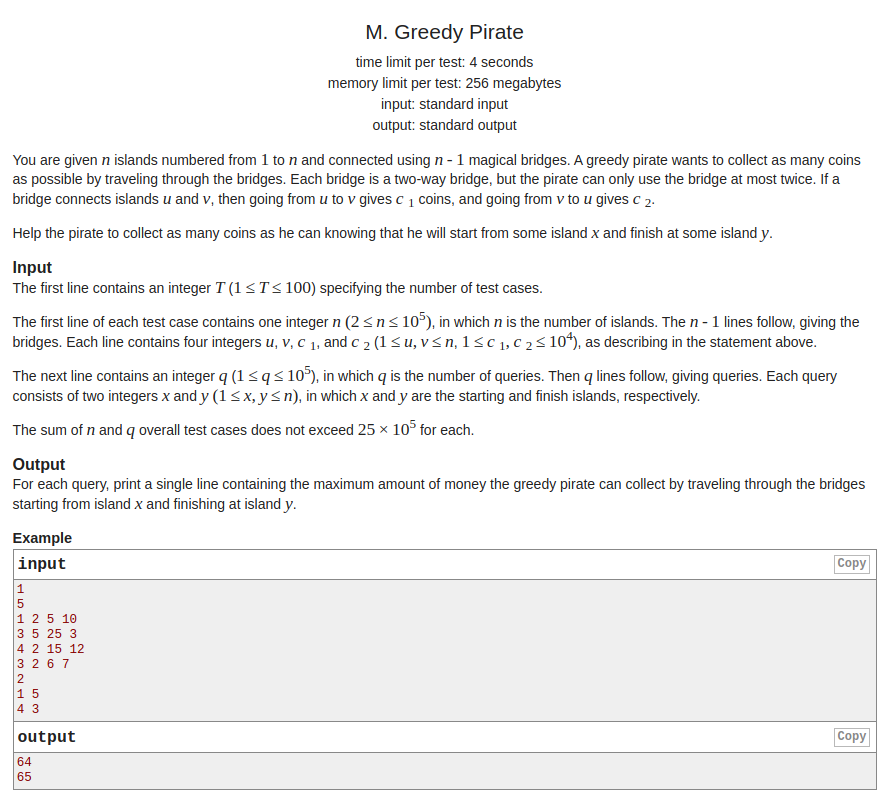
题意:有\(n\)个点,\(n-1\)条边,每条边正向和反向有两个权值,且每条边最多只能走两次,有\(m\)次询问,问你从\(u\)走到\(v\)的最大权值是多少.
-
题解:可以先在纸上画一画,不难发现,除了从\(u\)走到\(v\)的路径上的反向权值我们取不到,其他所有边的正反权值均能取到,所以答案就是:\(sum-u->v路径的反向权值\),问题也就转换成了求\(v->u\)的权值,那么这里我们就可以用LCA来求了.
首先,令一个点为根节点,然后求出\(v\)到根节点的距离和根节点到\(u\)的距离,再减去根节点到\(LCA(u,v)\)的正反权值,就是\(v->u\)的权值.
这题会卡读入,记得用scanf.
-
代码:
struct misaka{ int out; int val1,val2; }p; int t; int n,m; int sum; vector<misaka> V[N]; int fa[N][30]; int depth[N]; int lg[N]; int dis1[N],dis2[N]; bool st[N]; void dfs(int node){ //求每个节点到根节点的距离. st[node]=true; for(auto w:V[node]){ int now=w.out; int val1=w.val1; int val2=w.val2; if(st[now]) continue; dis1[now]=dis1[node]+val1; dis2[now]=dis2[node]+val2; dfs(now); } } void presol(int node,int fath){ fa[node][0]=fath; depth[node]=depth[fath]+1; for(int i=1;i<=lg[depth[node]]-1;++i){ fa[node][i]=fa[fa[node][i-1]][i-1]; } for(auto w:V[node]){ if(w.out!=node){ presol(w.out,node); } } } int LCA(int x,int y){ if(depth[x]<depth[y]){ swap(x,y); } while(depth[x]>depth[y]){ x=fa[x][lg[depth[x]-depth[y]]-1]; } if(x==y) return x; for(int k=lg[depth[x]]=1;k>=0;--k){ if(fa[x][k]!=fa[y][k]){ x=fa[x][k]; y=fa[y][k]; } } return fa[x][0]; } int main() { ios::sync_with_stdio(false);cin.tie(0); cin>>t; while(t--){ cin>>n; sum=0; for(int i=1;i<=n-1;++i){ int u,v,val1,val2; cin>>u>>v>>val1>>val2; p.out=v,p.val1=val1,p.val2=p.val2; V[u].pb(p); p.out=u,p.val1=val2,p.val2=p.val1; V[v].pb(p); } for(int i=1;i<=n;++i){ lg[i]=lg[i-1]+(1<<lg[i-1]==i); } dfs(1); presol(1,0); cin>>m; for(int i=1;i<=m;++i){ int u,v; cin>>u>>v; cout<<sum-(dis1[u]+dis2[v]-dis1[LCA(u,v)]-dis2[LCA(u,v)])<<endl; } } return 0; }
𝓐𝓬𝓱𝓲𝓮𝓿𝓮𝓶𝓮𝓷𝓽 𝓹𝓻𝓸𝓿𝓲𝓭𝓮𝓼 𝓽𝓱𝓮 𝓸𝓷𝓵𝔂 𝓻𝓮𝓪𝓵
𝓹𝓵𝓮𝓪𝓼𝓾𝓻𝓮 𝓲𝓷 𝓵𝓲𝓯𝓮


 浙公网安备 33010602011771号
浙公网安备 33010602011771号