Codeforces Round #655 (Div. 2) B. Omkar and Last Class of Math (数学)

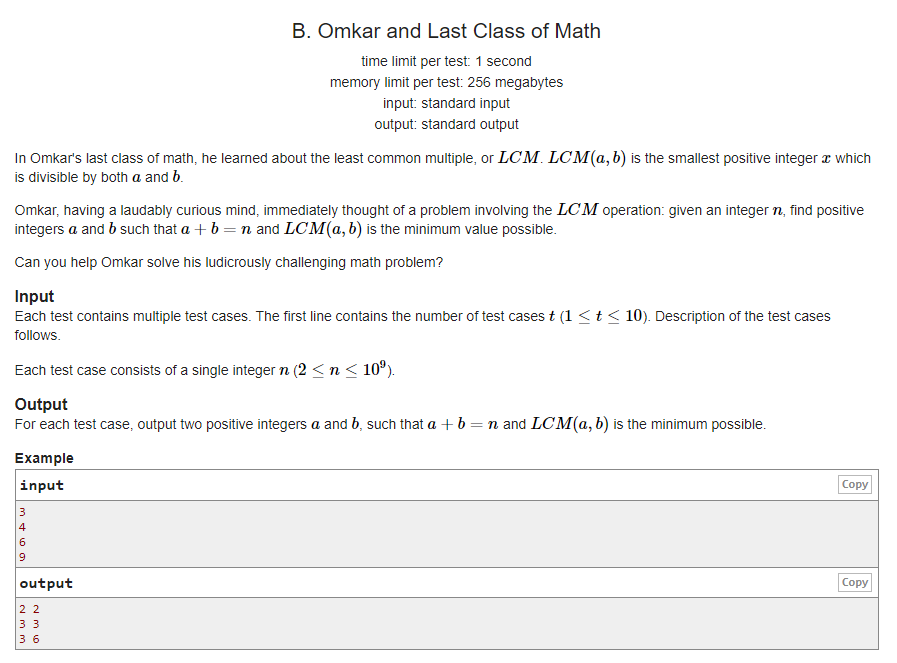
• 题意:给你一个正整数\(n\),求两个正整数\(a\)和\(b\),使得\(a+b=n\),并且\(LCM(a,b)\)要尽可能的小.

• 题解:首先对于偶数,构造\(\frac{n}{2}\)和\(\frac{n}{2}\)一定是最优解,对于奇数,我们去找除它本身的最大因子\(a\),为什么呢?

  ​ 我们假设\(a\)是\(n\)的一个真因子,那么\(a\)能整除\(n\),则\(a\)也一定能整除\(n-a\),那么它们的\(lcm(a,n-a)=n-a\),所以我们要让\(n-a\)尽可能小,即\(a\)要尽可能地大,所以我们要求\(n\)的最大因子即可.若无真因子,就直接输出\(1\)和\(n-1\).

• 代码;

  int t;
  int n;
   
  int main() {
      ios::sync_with_stdio(false);cin.tie(0);
    	cin>>t;
    	  while(t--){
    	  	cin>>n;
    	  	if(n%2==0){
    	  		cout<<n/2<<" "<<n/2<<endl;
    	  	}
    	  	else{
    	  		int p=1;
    	  		for(int i=2;i<=n/i;++i){
    	  			if(n%i==0){
    	  				p=n/i;
    	  				break;
    	  			}
    	  		}
    	  		cout<<p<<" "<<n-p<<endl;
    	  	}
    	  }
  
      return 0;
  }