2020牛客暑期多校训练营(第二场) F.Fake Maxpooling (单调队列)
-
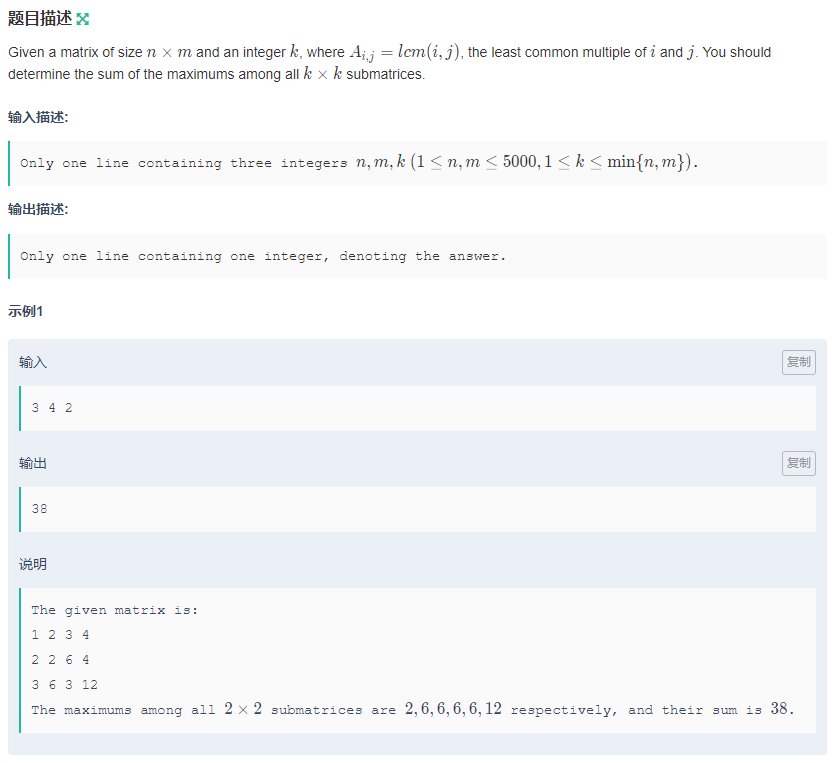
题意:有一个\(n\)x\(m\)的矩阵,\(A_{i,j}=lcm(i,j)\),对于每个\(k\)x\(k\)的子矩阵,其最大元素贡献给答案,求答案的最大值.
-
题解:矩阵构成我们直接\(i*j/gcd(i,j)\)即可,然后就要去找每个子矩阵中的最大元素.
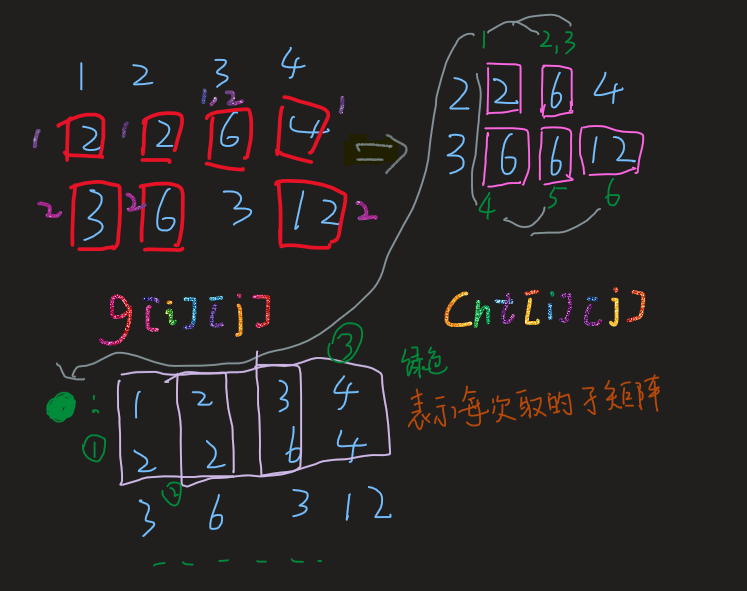
这题我们可以用单调队列来求,首先先对每一列维护长度为\(k\)的最大值,并且用数组记录前\(n-k+1\)行所对应的最大值,之后我们再对之前记录的数组的每一行维护最大值,然后贡献给答案.
如果真的不懂,建议去了解了解单调队列,这题基本上就是单调队列的裸题.
-
代码:
int n,m,k; int g[6000][6000]; int cnt[6000][6000]; int q[N]; int hh,tt; int main() { ios::sync_with_stdio(false);cin.tie(0); cin>>n>>m>>k; for(int i=1;i<=n;++i){ for(int j=1;j<=m;++j){ g[i][j]=i*j/__gcd(i,j); } } for(int j=1;j<=m;++j){ hh=1,tt=0; for(int i=1;i<=n;++i){ while(hh<=tt && g[q[tt]][j]<=g[i][j]) tt--; q[++tt]=i; if(hh<=tt && q[hh]<=i-k) hh++; if(i>=k) cnt[i-k+1][j]=g[q[hh]][j]; } } ll ans=0; for(int i=1;i<=n-k+1;++i){ hh=1,tt=0; for(int j=1;j<=m;++j){ while(hh<=tt && cnt[i][q[tt]]<=cnt[i][j]) tt--; q[++tt]=j; if(hh<=tt && q[hh]<=j-k) hh++; if(j>=k) ans+=cnt[i][q[hh]]; } } cout<<ans<<endl; return 0; }
𝓐𝓬𝓱𝓲𝓮𝓿𝓮𝓶𝓮𝓷𝓽 𝓹𝓻𝓸𝓿𝓲𝓭𝓮𝓼 𝓽𝓱𝓮 𝓸𝓷𝓵𝔂 𝓻𝓮𝓪𝓵
𝓹𝓵𝓮𝓪𝓼𝓾𝓻𝓮 𝓲𝓷 𝓵𝓲𝓯𝓮


 浙公网安备 33010602011771号
浙公网安备 33010602011771号