Codeforces Round #654 (Div. 2) D. Grid-00100 (构造)

• 题意:构造一个\(n\)x\(n\)只含\(0\)和\(k\)个\(1\)的矩阵,统计每一行每一列\(1\)的sum,然后构造一个权值最大行和最小行的差的平方加权值最大列和最小列的差的平方的最小和(\(f(A)=(max(R)-min(R))^2+(max(C)-min(C))^2\)的最小值).

• 题解:假如\(k\ mod\ n=0\)的话,那么最小值一定是0,否则一定是2,直接上图吧.

  ​ 1.k%n=0:

  ​

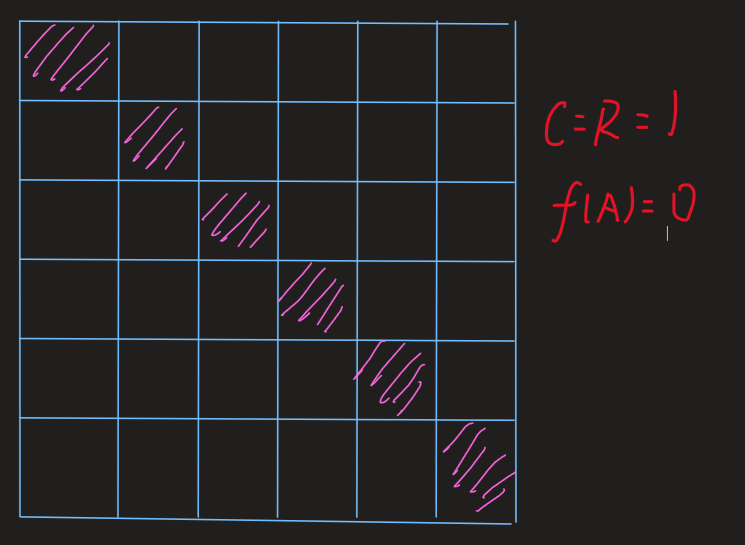
  2.k%n!=0:

  

  这样的话,规律应该显而易见了吧,我们沿着对角线构造,然后取余,填填补补即可,具体的看代码吧.

• 代码:

  int t;
  int n,k;
  int a[400][400];
   
  int main() {
      ios::sync_with_stdio(false);cin.tie(0);
    	cin>>t;
    	 while(t--){
    	 	cin>>n>>k;
    	 	me(a,0,sizeof(a));
    	 	if(k%n==0){
    	 		cout<<0<<endl;
    	 	}
    	 	else cout<<2<<endl;
    	 	for(int i=0;i<k%n;++i){
    	 		for(int j=i;j<=i+k/n;++j){
    	 			a[i][j%n]=1;
    	 		}
    	 	}
    	 	for(int i=k%n;i<n;++i){
    	 		for(int j=i;j<i+k/n;++j){
    	 			a[i][j%n]=1;
    	 		}
    	 	}
    	 	for(int i=0;i<n;++i){
    	 		for(int j=0;j<n;++j){
    	 			cout<<a[i][j];
    	 		}
    	 		cout<<endl;
    	 	}
    	 }
   
      return 0;
  }