AtCoder Beginner Contest 173 E - Multiplication 4 (思维)

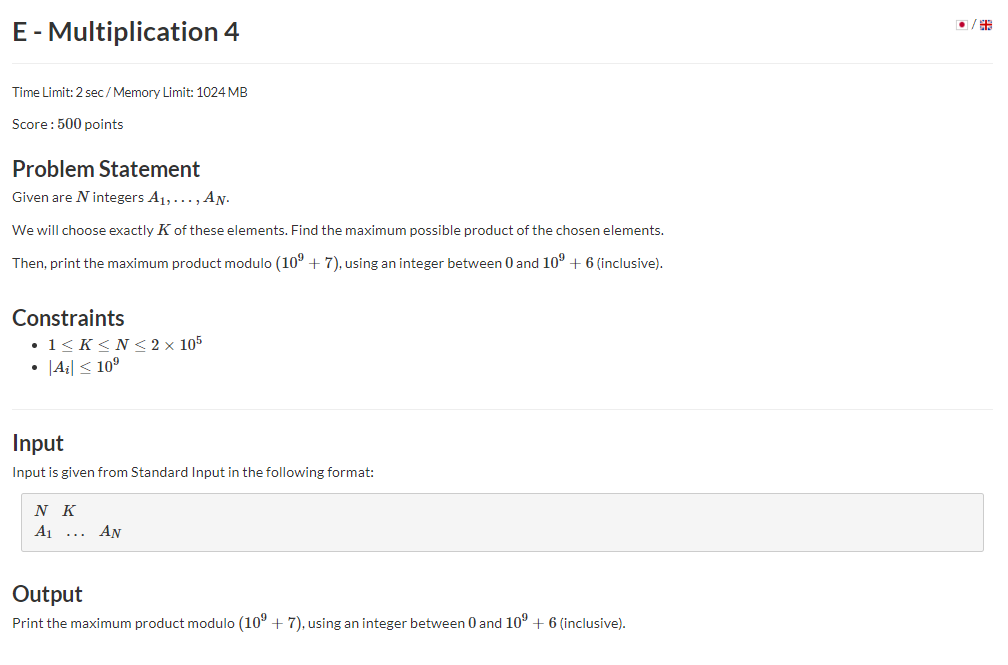
• 题意:有\(n\)个数,从中选\(k\)个数累乘,求最大的乘积\((mod\ 10^9+7)\).

• 题解:

  1.假如全是负数,并且选奇数个,那么从小到大选.

  2.否则,考虑当前状态,假如\(k\)是奇数,那么我们先选一个最大的,然后再选两个最大的正数相乘或者两个负数相乘后最大,每次这样选即可.

• 代码:

  int n,k;
  ll a[N];
  ll mp[N];
   
  bool cmp(ll x,ll y){
  	return abs(x)<abs(y);
  }
  
  int main() {
      ios::sync_with_stdio(false);cin.tie(0);
    	cin>>n>>k;
    	for(int i=1;i<=n;++i){
    		cin>>a[i];
    		if(a[i]>=0) mp[1]++;
    		else mp[2]++; 
    	}
    	int l=1,r=n;
    	ll ans=1;
    	if(mp[1]==0 && k%2==1){
    		sort(a+1,a+1+n,cmp);
    		for(int i=1;i<=k;++i){
    			ans=a[i]*ans%mod;
    		}
    	}
    	else{
    		sort(a+1,a+1+n,greater<int>());
    		while(k>0){
    			if(k%2==1) ans=ans*a[l++]%mod,m--;
    			else if(k>=2){
    				if(a[l]*a[l+1]>=a[r]*a[r-1]){
    					ans=ans*a[l]%mod*a[l+1]%mod;
    					l+=2;
    					k-=2;
    				}
    				else{
    					ans=ans*a[r-1]%mod*a[r]%mod;
    					r-=2;
    					k-=2;
    				}
    			} 
    		}
    	}
  
    	cout<<(ans%mod+mod)%mod<<endl;
  
      return 0;
  }