Codeforces Round #646 (Div. 2) B. Subsequence Hate (思维,前缀和)
-
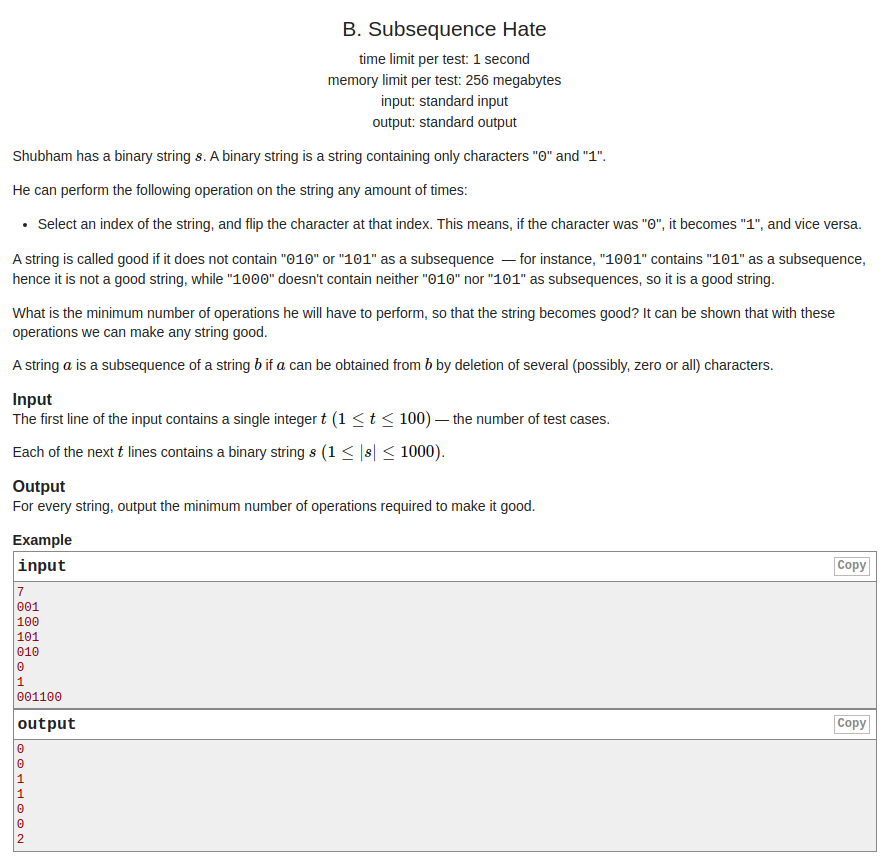
题意:给你一个只含有\(0\)和\(1\)的字符串,每次操作可以将\(0\)改成\(1\)或\(1\)改成\(0\),问最少操作多少次,使得子序列中不含有\(010\)和\(101\).
-
题解:仔细想一想不难发现,构造后的字符串要么全是\(1\)和\(0\),要么就是\(000....111\)和\(111...000\),我们对\(0\)求一个前缀和,判断一下这些情况,更新最小值即可.
-
代码:
#include <iostream> #include <cstdio> #include <cstring> #include <cmath> #include <algorithm> #include <stack> #include <queue> #include <vector> #include <map> #include <set> #include <unordered_set> #include <unordered_map> #define ll long long #define fi first #define se second #define pb push_back #define me memset const int N = 1e6 + 10; const int mod = 1e9 + 7; const int INF = 0x3f3f3f3f; using namespace std; typedef pair<int,int> PII; typedef pair<ll,ll> PLL; int t; int pre[N]; string s; int main() { ios::sync_with_stdio(false);cin.tie(0); cin>>t; while(t--){ cin>>s; s=" "+s; me(pre,0,sizeof(pre)); int len=s.size(); int cnt0=0,cnt1=0; for(int i=1;i<len;++i){ if(s[i]=='0'){ cnt0++; pre[i]=pre[i-1]+1; } else{ cnt1++; pre[i]=pre[i-1]; } } int ans=min(cnt0,cnt1); for(int i=1;i<len;++i){ ans=min(ans,pre[i]+(len-1-i-(pre[len-1]-pre[i]))); } for(int i=1;i<len;++i){ ans=min(ans,i-pre[i]+pre[len-1]-pre[i]); } printf("%d\n",ans); } return 0; }
𝓐𝓬𝓱𝓲𝓮𝓿𝓮𝓶𝓮𝓷𝓽 𝓹𝓻𝓸𝓿𝓲𝓭𝓮𝓼 𝓽𝓱𝓮 𝓸𝓷𝓵𝔂 𝓻𝓮𝓪𝓵
𝓹𝓵𝓮𝓪𝓼𝓾𝓻𝓮 𝓲𝓷 𝓵𝓲𝓯𝓮


 浙公网安备 33010602011771号
浙公网安备 33010602011771号