JDK8;HashMap:再散列解决hash冲突 ,源码分析和分析思路
JDK8中的HashMap相对JDK7中的HashMap做了些优化。
接下来先通过官方的英文注释探究新HashMap的散列怎么实现
先不给源码,因为直接看源码肯定会晕,那么我们先从简单的概念先讲起
(如果你不想深入理解 请不要看括号里的内容,可以简化阅读过程)
首先,有一个问题:假如我们现在有一个容量为16的数组,现在我想往里面放对象,我有15个对象。
怎么放进去呢???
其实要解决一个问题就够了:对象要放在哪个下标???
当然最简单的方法是从0下标开始一个一个挨着往后放

看,这样就把你们的对象放满整个数组了,一个位置也没有浪费~
但是有17个对象呢?
无论无何必须有两个对象在同一个槽位(槽位指的是数组中某个下标的空间)了,如果不扩充数组的大小的话
那我们采取的策略最简单的是像上面一样先塞满数组,最后一个对象随机放到一个位置,用链表的形式把他挂在数组中某个位置的对象上。
(较新版本的JDK中 如果链表太长会变成树)

但是如果现在我们有20个对象呢???50个对象呢???100个,1000个对象呢???
每个槽位需要承受的对象数量会越来越多,如果只是一味地挂对象,而不采取合适的策略确定要加上去的对象到底放在哪个位置的话,很有可能出现下面这种状况。
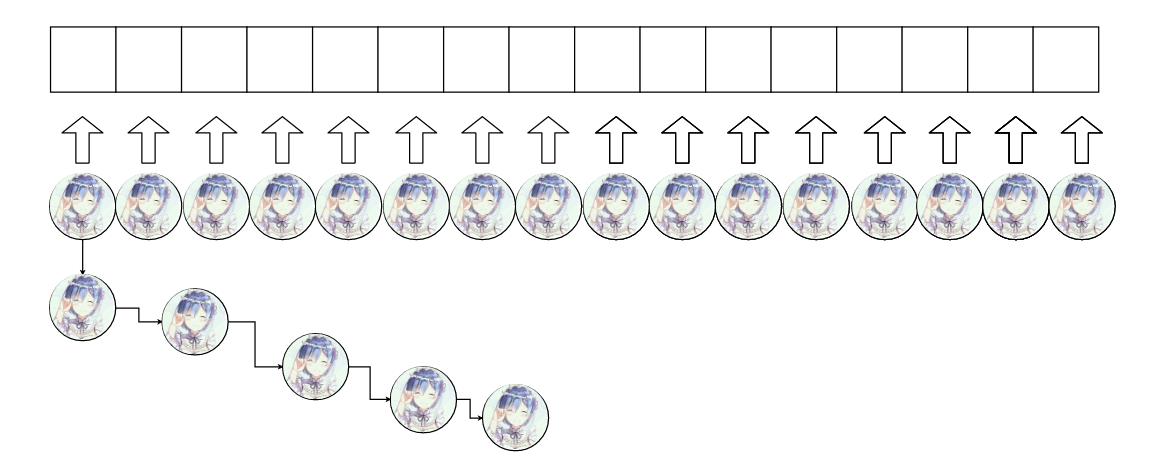
那么当我们查找一个对象的时候可能遇到这种情况,
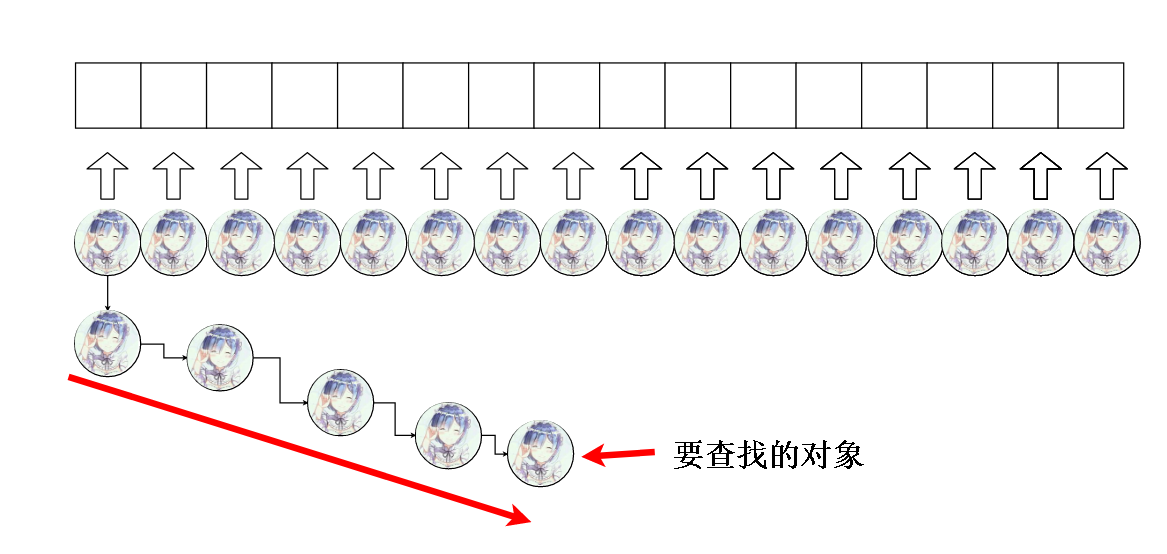
这样的话,查询效率十分低下,我们希望加上去的对象在整个数组上呈均匀分布的趋势,这样就不会出现某个槽承受了很多对象但是有的槽位承受很少对象,甚至只有一个对象的情况。
下面是我们希望的结果。
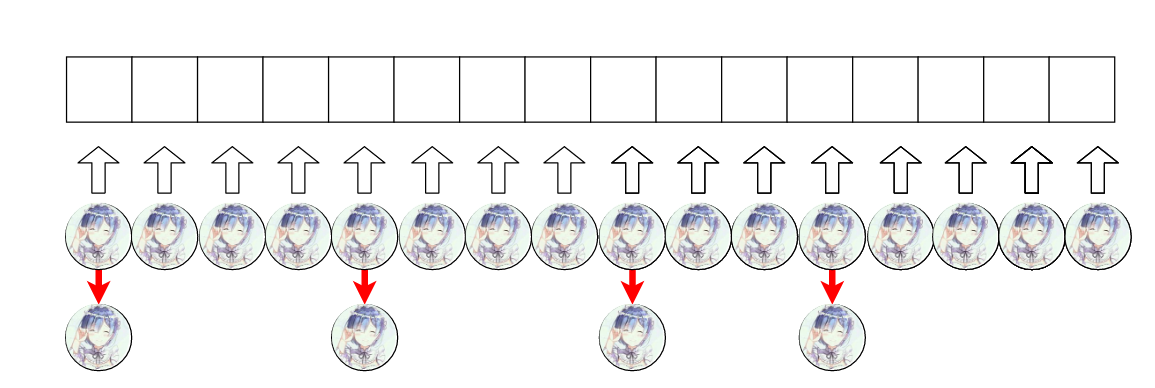
因为要查询的话最多查两次就能查到我们想要的对象了。
这样我们就不得不决定,要加入的对象在数组的下标了!
怎么确定下标呢?有一种确定下标的方法,这种确定下标的方法(算法)叫做散列。很形象吧,打散,列开。
散列的过程就是通过对象的特征,确定他应该放在哪个下标的过程。
那这个特征是什么呢???
哈希码!(hashCode的翻译)
java每个对象都有一个叫"hashCode"的标签码 和他对应,当然这个hashCode不一定是唯一的。
(在HashMap的源码中调用了key.hashCode()来获得hashCode,请注意,因为实际调用到的是运行时对象所属类的方法
[比如类A继承了类Object,A重写了Object的hashCode()方法,Object ob = new A(); ,ob.hashCode();调用的实际是类A重写后的hashCode方法
所以我们可以通过重写 hashCode() 方法来返回我们想要的hashCode值]
所以不同对象的hashCode 可能是一样的,取决于类怎么重写hashCode()
)
我们的问题可以简化为,怎么把我们的hashCode映射到下标的二进制码上呢?
现在假设我们的 hashCode 是8位的 (实际上是32位的),比如下面就是一个对象a 的hashCode

假如我们的数组大小是16,那么我们要根据hashCode 确定好数组下标,下标的范围是0~15.
该怎么确定呢?我们可以用直接映射的方法
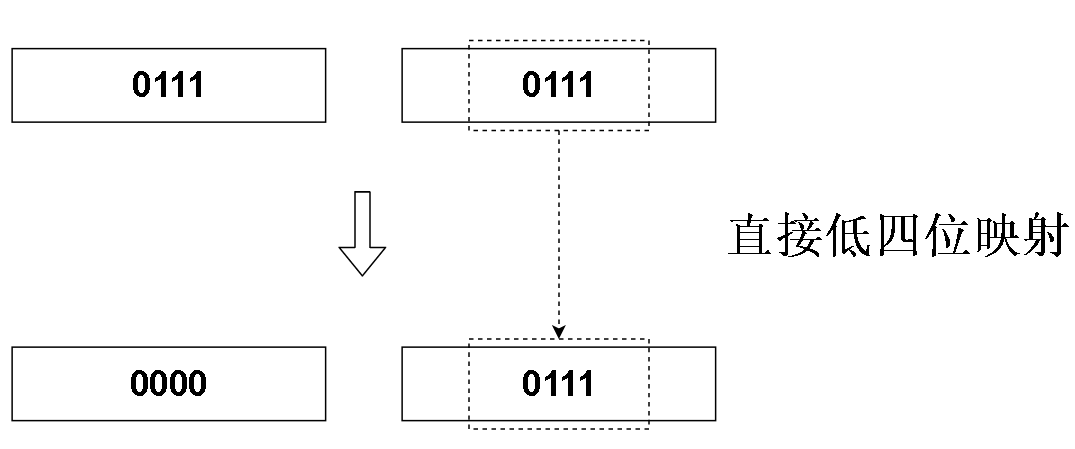
我们发现,把hashCode 的二进制码直接映射到数组下标的二进制码上,直接把高位全部置为0,好像可以喔。
而且 因为我们用低四位去映射,所以范围会保持在0~15间,所以最后映射的结果总是没有超出范围
这样的话,上图的hashCode 的数组下标就是 7( 1 + 2 + 4 = 7, 0111的十进制=7)
但是,进一步观察,我们发现,无论高位怎么样,只要低位相同,都会映射到同一个数组下标上。

高位有 2 ^ 4 = 16 种情况,这16种情况都会瞄准同一个数组下标,何况实际上我们的hashCode是32位的,这样的话就有 2 ^ (32 - 4) = 2 ^ 28 种冲突
出现了我们之前担心的场景,许多甚至所有对象组成一条链表挂在一个位置上,这样查询效率十分低下。
这种对不同对象进行散列,但是最后得到的下标相同的情况称为hash冲突,也可以称为散列冲突,其实散列就是hash翻译过来的。
好的,正片开始!
我们来看看JDK8中的HashMap是怎么解决这种冲突的。
首先我们要知道,JDK8是怎么执行散列的
JDK8使用了掩码,即是下文注释中将提到的用来masking的数值
这个掩码是根据HashMap存储对象的数组的大小决定的,图中table就是我们所说的hash表,n - 1 被作为掩码和 传进来的hash值(也就是hashCode)
进行 & 运算。
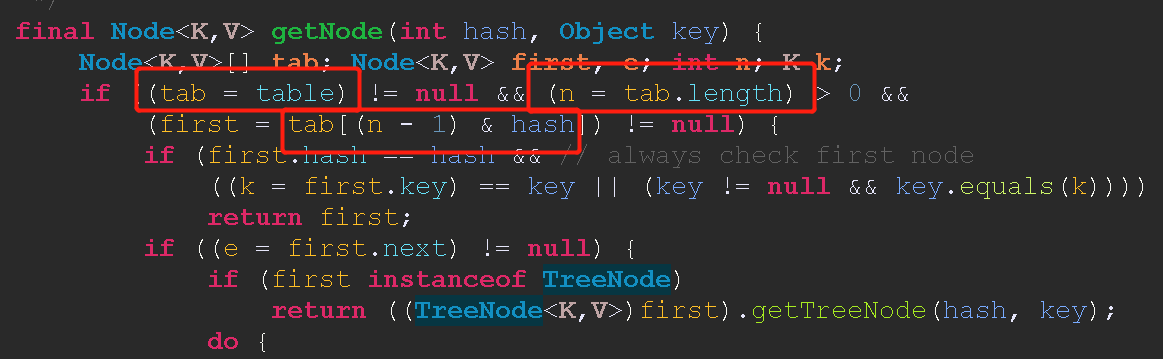
看下面一个例子更明了一点。
比如大小为 32 的hash表
32的二进制数是 0010 0000
那么32 - 1 = 31 就是 0001 1111
0001 1111 & A 会得到什么呢,0001 1111 像一块掩布一样,将和他 & 的数 A 的前三位都遮住,全部变成0,其他位不变,所以被称为掩码。
比如 A = 1101 0101
因为我们的掩码前三位全是0 那么他就会把A的前三位全部掩盖掉,掩码后面的1,和A对应位 & 之后保持不变
现在再来看看官方源码的hashCode是怎么减少冲突的。
来看hash 方法上的一段注解, hash方法是把hashCode再散列一次,把散列hashCode后的值作为返回值返回,以此再次减少冲突,而过程是把高位的特征性传到低位。
每个 [] 中的内容都是对前面一小段的解释,如果嫌麻烦可以直接读解释,不读英文
/**
* Computes key.hashCode() [计算得出hashCode 不归hash函数管] and spreads (XORs) higher bits of hash
* to lower[把高位二进制序列(比如 0110 0111 中的 0110) , 的特征性传播到低位中,通过异或运算实现]. Because the table uses power-of-two masking[HashMap存储对象的数组容量经常是2的次方,这个二的次方(比如上面是16 = 2 ^ 4) 减1后作为掩码], sets of
* hashes that vary only in bits above the current mask will
* always collide[在掩码是2^n - 1 的情况下,只用低位的话经常发生hash冲突,见上述例子]. (Among known examples are sets of Float keys
* holding consecutive whole numbers in small tables.) So we
* apply a transform that spreads the impact of higher bits
* downward[将高位的特征性传播到低位去]. There is a tradeoff between speed, utility, and
* quality of bit-spreading[但是这种特性的传播会带来一定的性能损失]. Because many common sets of hashes
* are already reasonably distributed (so don't benefit from
* spreading)[因为有的hashCode他们的低位已经足够避免多数hash冲突了,比如我们的hashCode是八位的
并且我们的数组大小是((2 ^ 8) - 1) (0111 1111) 那么只有两种冲突情况而已,0mmm mmmm 和 1mmm mmmm 会冲突,每次进行插入元素或者查找元素都要调用hash函数再一次散列hashCode,显然不划算], and because we use trees to handle large sets of
* collisions in bins[其实之前说的若干对象变成链表挂在一个数组位置上,已经是一种解决冲突的办法了], we just XOR some shifted bits in the
* cheapest possible way to reduce systematic lossage[所以我们只用最简单的异或运算来减少冲突,减少性能损失], as well as
* to incorporate impact of the highest bits that would otherwise
* never be used in index calculations because of table bounds[把本来可能因为数组大小限制而用不上(上面说的就算高位不同,只要低位相同就可以指向同一个数组下标),的高位也用上].
*/
static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}
什么意思呢?什么叫做把高位的特征也用上?
比如我们之前说的。当我们有一个大小为16的数组,下面是两个对象的hashCode
0110 0111
1100 0111
如果我们直接用这两个未经hash函数处理的hashCode 通过JDK的方法得出下标:

n = 16
16 = 0001 0000
16 - 1 = 15 = 0000 1111
hash(这是上图蓝字变量) = hashCode(未经hash函数再散列)
0110 0111 & 0000 1111 = 0000 0111 ------ 7
1100 0111 & 0000 1111 = 0000 0111 ------ 7
求得同一个下标,显然冲突了,就算两个hashCode他们的高位不同,但还是会冲突
现在我们用上高位的特性,

因为本来hashCode是32位的,所以上面 >>> 的是16,也就是高一半的位移到低一半去
而我们设置的hashCode 是8位的,所以上面的 >>> 的应该是 4
hash (上面蓝字变量) = hash (hashCode) ------ hash函数对hashCode 再散列
对应过程如下图
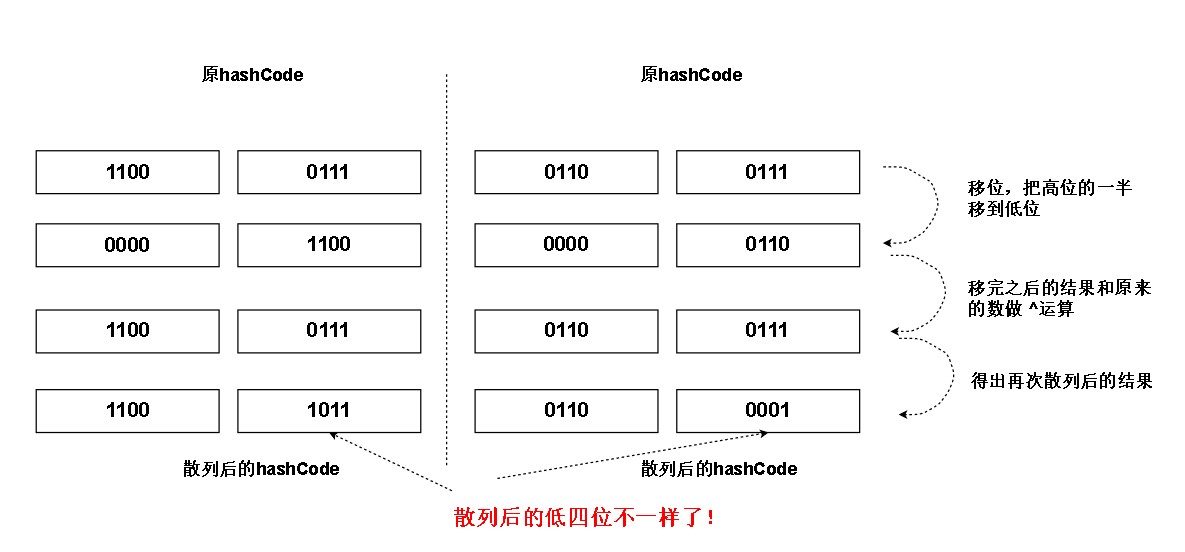
正如我们所见,原本冲突的低四位,把高位的特征传到他们上面后,他们不冲突了!
当我们对这些再散列后的结果用掩码掩掉不必要的高位之后(见上面的红框框图)(比如高四位),剩下的是
0000 1011
0000 0001
对应的数组下标是 11 和 1
解决了冲突!
关于HashMap的扩容篇正在路上~




 浙公网安备 33010602011771号
浙公网安备 33010602011771号