交叉熵损失(cross-entropy)和折页损失(Hinge loss)
-
Cross-Entropy Loss
假设![]() 是一对训练样本,
是一对训练样本,![]() 是训练数据,
是训练数据,![]() 是对于分类的one hot向量(该向量只有真实分类的参数为1,其余位数均为0)。假设通过softmax算得预测值
是对于分类的one hot向量(该向量只有真实分类的参数为1,其余位数均为0)。假设通过softmax算得预测值![]() ,则损失表示如下:
,则损失表示如下:
![]()
很明显的我们看到这个损失涉及到了哪些参数,只有两个,那就预测值和真实值。这里的真实值采用one hot encoding,预测值则必须是概率分布。
例如
![]()
在这里我们只需要关注y的1数位,因为其他位数都为0,乘积也就为0
那么,我们可以得到![]()
-
Hinge Loss
很显然,我们分析交叉熵损失,有些缺点是不可避免的。因为其预测值是概率分布,导致不可避免的计算瓶颈,当我们遇到的类别非常庞大时,计算量的代价是巨大的。虽然概率分布的形式最为直观,但其实可以直接使用得分来判断具体的分类。
损失的表达式计算为:
![]()
很容易发现相对于交叉熵,折页仅仅多了一个参数。三个参数分别是![]() (代表其他所有类的得分),
(代表其他所有类的得分),![]() (真实类别的得分)
(真实类别的得分)
这里![]() 简要的说明,为什么要在这里添加这个参数呢?例如当最高得分的分类得到了45分,而第二高得到了43分,显然得到的结果是不令人信服的。所以在这里加入该参数,相当于给最大的值一个区间,拉开与其他分类的差距。
简要的说明,为什么要在这里添加这个参数呢?例如当最高得分的分类得到了45分,而第二高得到了43分,显然得到的结果是不令人信服的。所以在这里加入该参数,相当于给最大的值一个区间,拉开与其他分类的差距。
通过分析,什么时候损失会变为0呢,就是当真实类别的得分要比其他所有分类都要到高的时候,这显然是符合现实场景的。 -
计算与比较
![]()
那么给定了以上的情形,真实类别先定位y[2],也就是最后一个类别。面对这种的情况,两种损失到底应该如何计算呢? -
首先来计算Hinge loss,假设情形为支持向量机
![]()
-
再来计算Cross-Entropy Loss,假设使用softmax进行激活
首先还是计算三个类别的输出
![]()
接着输出经过exp
![]()
再进行归一化
![]()
在这里,分类是第二类,所以其他类都为0,可以轻松得到结果
![]()



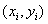 是一对训练样本,
是一对训练样本,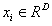 是训练数据,
是训练数据,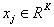 是对于分类的one hot向量(该向量只有真实分类的参数为1,其余位数均为0)。假设通过softmax算得预测值
是对于分类的one hot向量(该向量只有真实分类的参数为1,其余位数均为0)。假设通过softmax算得预测值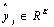 ,则损失表示如下:
,则损失表示如下: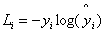

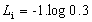
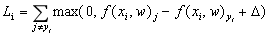
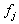 (代表其他所有类的得分),
(代表其他所有类的得分),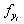 (真实类别的得分)
(真实类别的得分) 简要的说明,为什么要在这里添加这个参数呢?例如当最高得分的分类得到了45分,而第二高得到了43分,显然得到的结果是不令人信服的。所以在这里加入该参数,相当于给最大的值一个区间,拉开与其他分类的差距。
简要的说明,为什么要在这里添加这个参数呢?例如当最高得分的分类得到了45分,而第二高得到了43分,显然得到的结果是不令人信服的。所以在这里加入该参数,相当于给最大的值一个区间,拉开与其他分类的差距。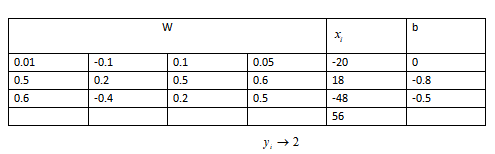
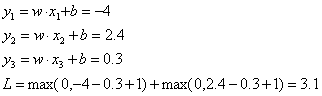
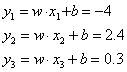
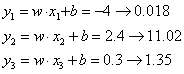
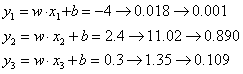
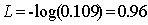

 浙公网安备 33010602011771号
浙公网安备 33010602011771号