8.15小记

8.15

麻麻的，最近诸事不顺，人都快要挂掉了。

没办法，想随便写点东西转移下注意力。正好之前似乎碰见了一道题可以进行深♂入地研究，索性就这样瞎写个题解。

题意

给定一个圆，圆上有\(n\)个点，点之间两两连线，求圆被划分的最大区域数。

solution

首先，介绍一下一个相关的定理。

欧拉公式：

\(V-E+F=2\)

其中\(V\)是面数，\(E\)是边数，\(F\)是点数。

这里会用到他的二维形式：

\(V-E+F=1\)

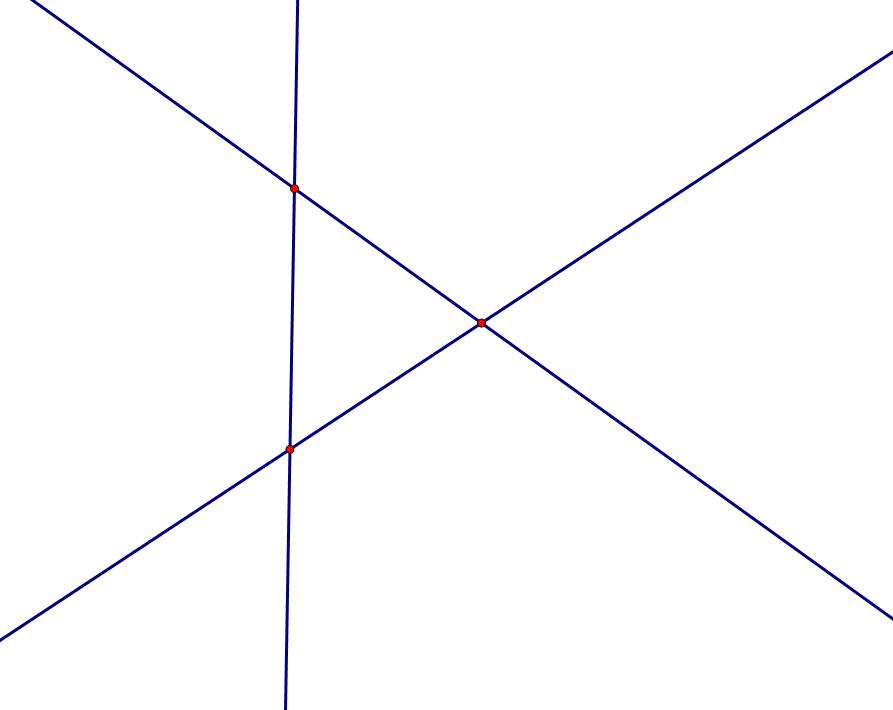
举个例子，假设我怕们有这样一张图：

那么，\(V=7，E=9，F=3，7-9+3=1\)。

可以简单证明一下，考虑数学归纳法：

首先一根线的情况是成立的。那么我们考虑在某一种情况下这个定理成立。我们尝试在图中添加一条线。然后，想象这根线从一端延伸到另一端，将这根线与其他已经存在的线的交点"放大"。

这时共两种情况：

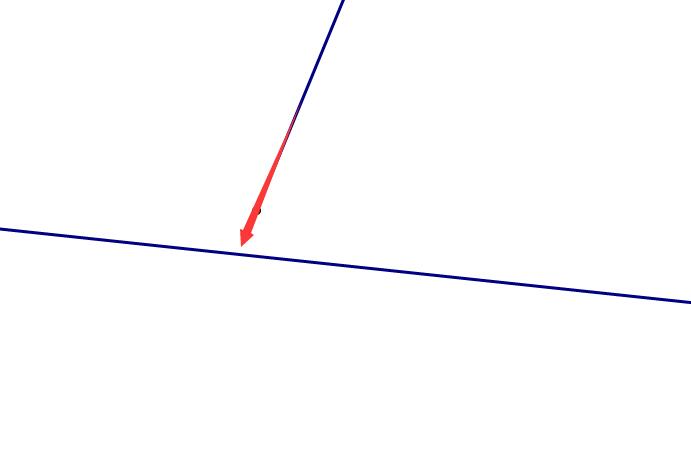
• 这个交点之前不存在，类似这样：

  

  那么，加了这条现之后的影响是\(V+1，E+2，F+1\)。仍然符合公式。

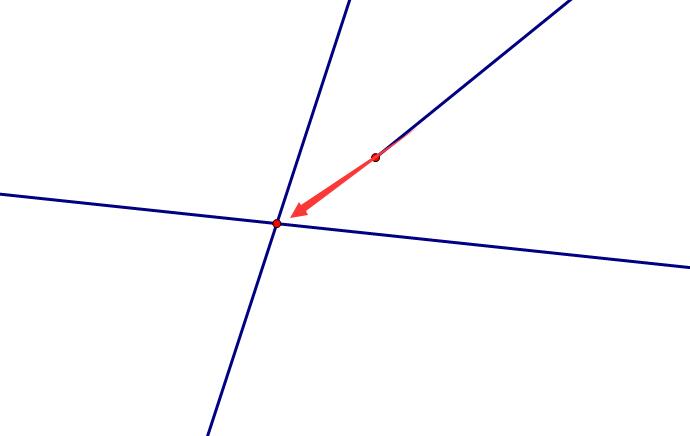
• 这个交点之前已经存在，类似这样：

  

  那么，加了这条现之后的影响是\(V+1，E+1，F+0\)。仍然符合公式。

• 所以，可以有一般情况推到任意情况，证毕，所以\(V=E-F+1\)。

有了这个定理，我们就可以愉♂快地开始做题了。

我们考虑由\(n\)个点的情况推到\(n+1\)个点的情况。

举个例子，假设我们已经加了\(3\)个点，\(V=4，E=6，F=3\)：

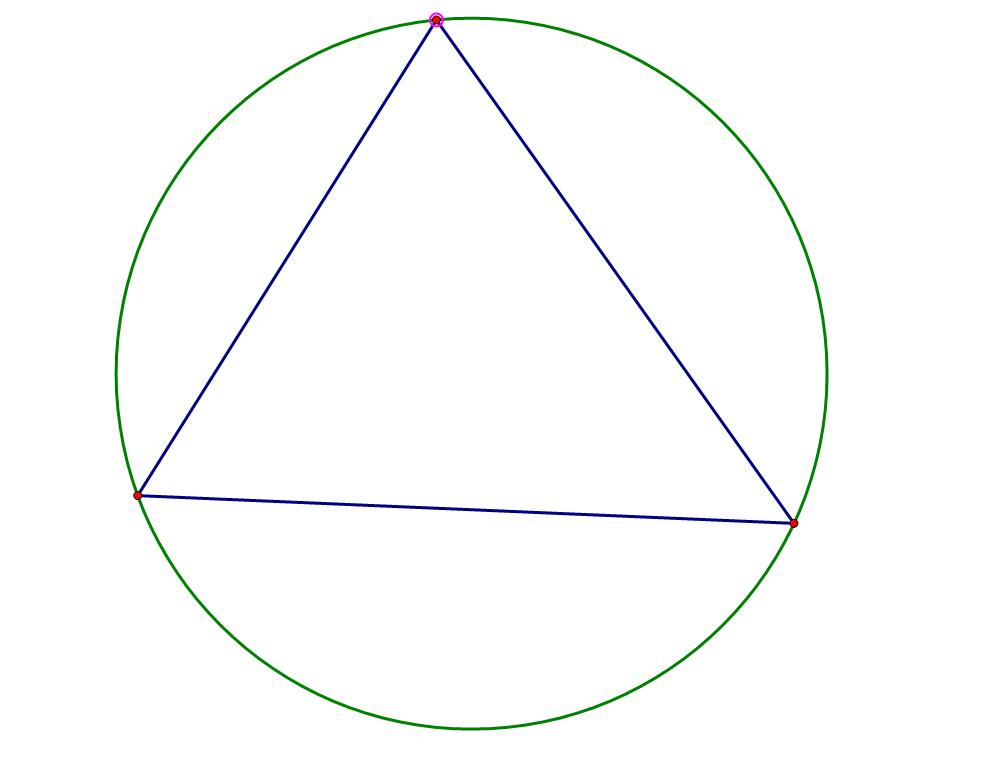
这时，再加入一个点，\(F+1，E+1\)，所以\(V\)不变，此时\(V=4，E=7，F=4\)：

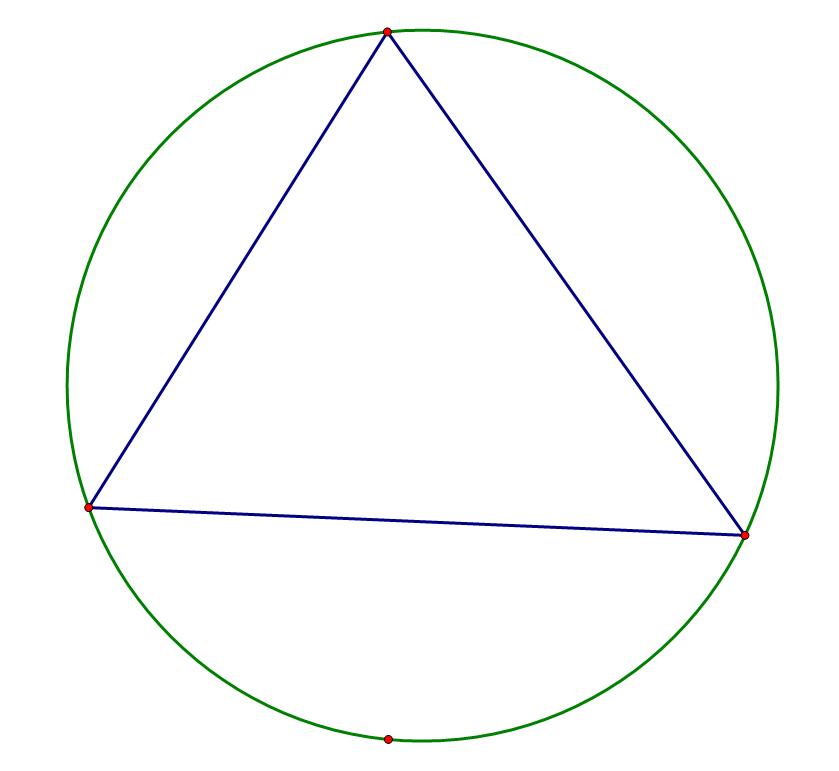
我们尝试让他与前面\(3\)个点连线，考虑\(E\)和\(F\)分别的变化：

第一条，\(E+1，F+0\)，所以\(V+1\)，此时\(V=5，E=8，F=4\)。

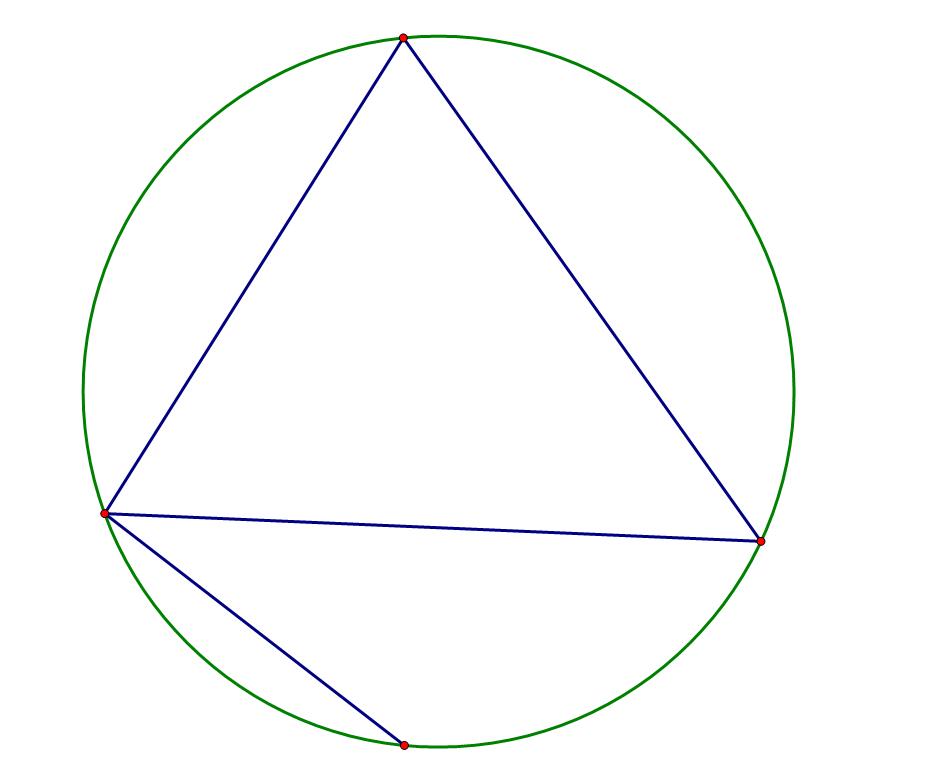
第二条，\(E+3，F+1\)，所以\(V+2\)，此时\(V=7，E=11，F=5\)。

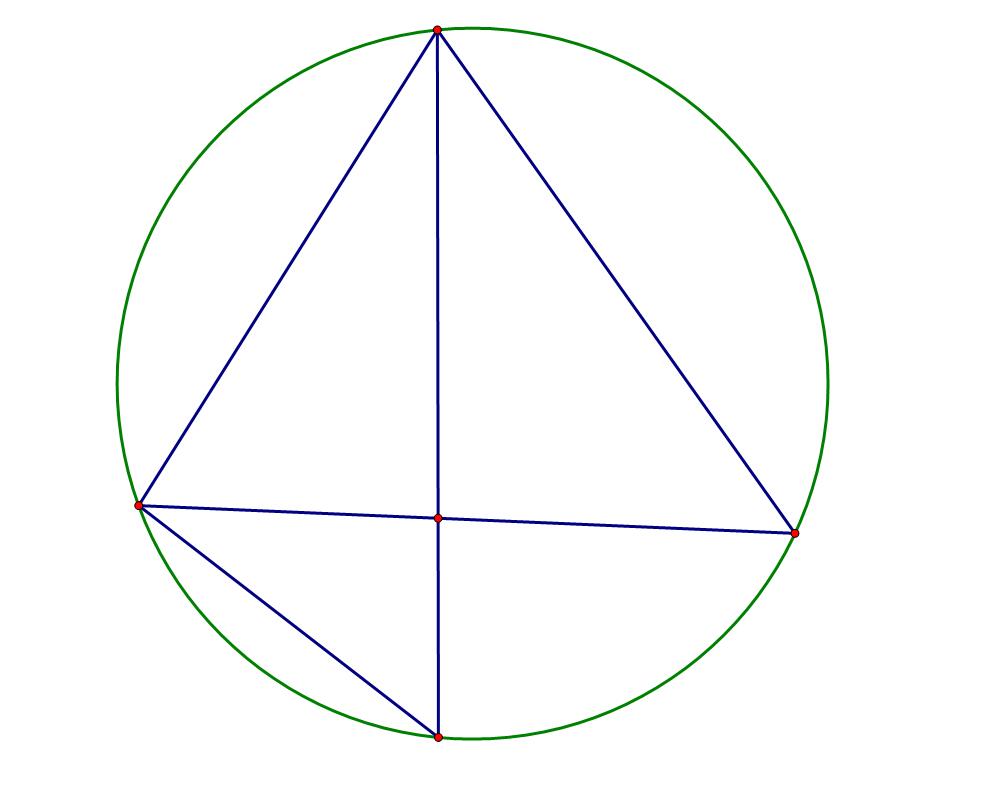
第三条，与第一条类似，\(E+1，F+0\)，所以\(V+1\)，此时\(V=8，E=12，F=5\)。

至此，我们将\(3\)个点的情况拓展到了\(4\)个点的情况。

现在，我们考虑更一般的例子，也就是\(n\)个点如何拓展到\(n+1\)个点。

仍然考虑在\(n\)个点的图上加入一个新的点，并与其他\(n\)个点依次连线。

我们将连线一次一次拆分出来看。

假如某次连线左边有\(i\)个点，那么右边就有\(n-1-i\)个点：

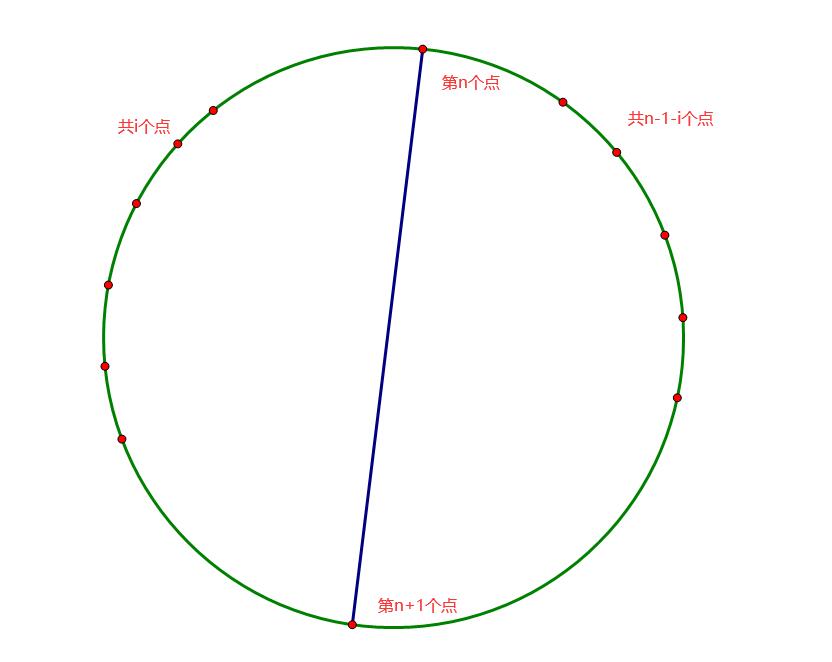
先考虑\(E\)的变化。

每当左边某个点与右边某个点有连线的话这条新的线所产生的新边就会\(+2\)：

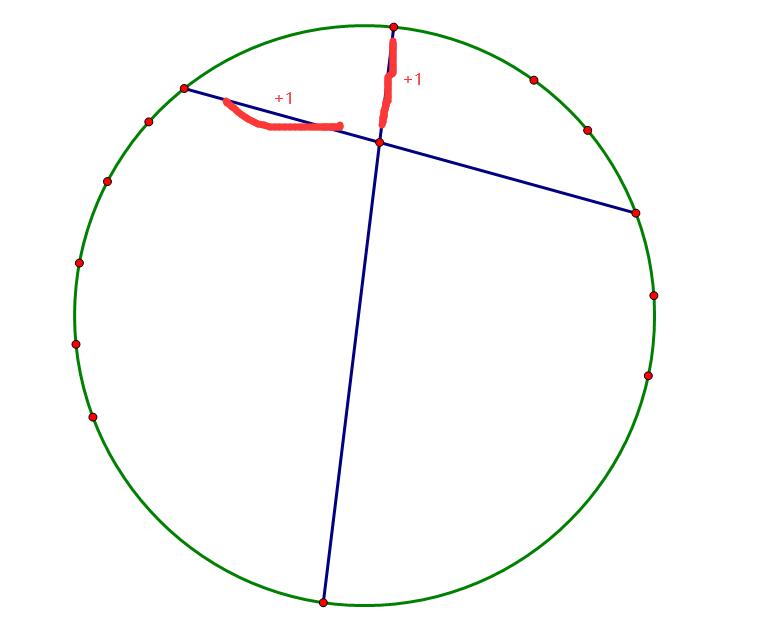
所以\(E+2i(n-1-i)\)。

再考虑\(F\)的变化。

类似的，每当左边某个点与右边某个点有连线的话这条新的线所产生的新点就会\(+1\)：

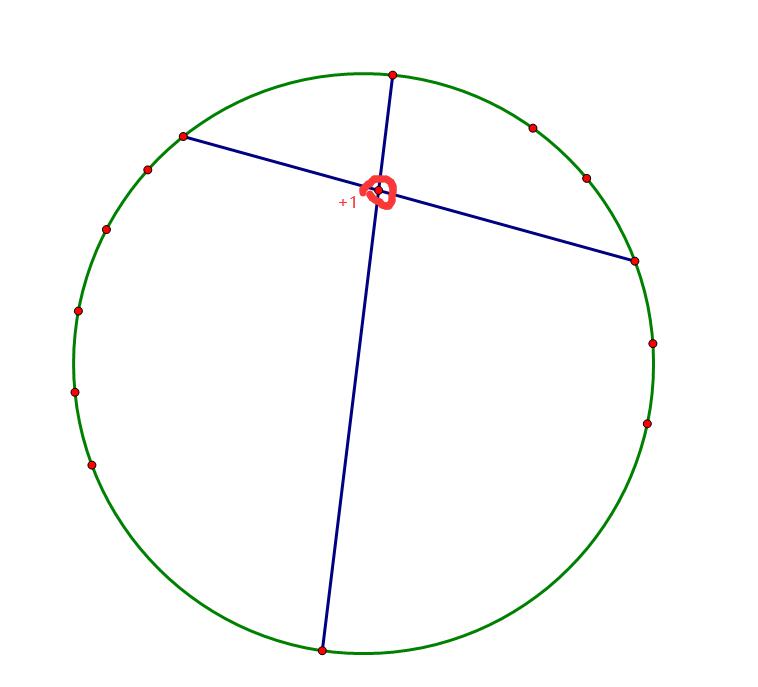
所以，\(F+i(n-1-i)\)。

但是这条边本身就会\(E+1\)。

所以这一次操作对\(V\)的影响为\(V+i(n-1-i)+1\)。

即，加了这条边后，产生的新面数为\(i(n-1-i)+1\)。

那么我们将所有贡献加起来，当加入第\(n+1\)个点时，产生的新面数为：

\[\sum_{i=0}^{n-1}{[i(n-1-i)+1]}\\ =\sum_{i=0}^{n-1}{[i(n-1-i)]}+n \]

由于我们加了一个新点，但这个新点同时也让圆上的边多了一条，所以实际贡献为：

\[\sum_{i=0}^{n-1}{[i(n-1-i)]}+n \]

如果我们令\(a_n\)为\(n\)个点时的答案，那么我们就得到了递推式：

\[a_{n+1}=a_n+\sum_{i=0}^{n-1}{[i(n-1-i)]}+n \]

其中，\(a_1=1\)。

所以，可以得到\(a_n\)的通项公式：

\[a_n=\sum_{i=1}^{n-1}{\{\sum_{j=0}^{i-1}{[j(i-1-j)}]+i\}}+a_1\\ =\sum_{i=1}^{n-1}{\sum_{j=0}^{i-1}{[j(i-1-j)}]}+\frac{n(n-1)}{2}+1\\ =\sum_{i=0}^{n-2}{\sum_{j=0}^{i}{[j(i-j)}]}+\frac{n(n-1)}{2}+1 \]

其实有这个通项已经差不多了，不过我们并不满足于此。

这个通项的瓶颈在于：

\[\sum_{i=0}^{n-2}{\sum_{j=0}^{i}{[j(i-j)}]} \]

如果我们能求得他的通项那么再好不过了。

考虑令\(\displaystyle b_n=\sum_{i=0}^{n}{[i(n-i)]}\)。

那么\(\displaystyle \sum_{i=0}^{n-2}{b_i}\)即为所求式子。

现在考虑求\(b_n\)通项，我们希望整出一个\(b_n\)的递推式，即：

\[b_n=b_{n-1}+f(n) \]

所以：

\[f(n)=b_{n}-b_{n-1}\\ =\sum_{i=0}^{n}{[i(n-i)]}-\sum_{i=0}^{n-1}{[i(n-1-i)]}\\ =\sum_{i=0}^{n-1}{[i(n-i)]}-\sum_{i=0}^{n-1}{[i(n-1-i)]}\\ =\sum_{i=0}^{n-1}{[i(n-i)-i(n-1-i)]}\\ =\sum_{i=0}^{n-1}i\\ =\frac{n(n-1)}{2}\\ =\frac{1}{2}n^2-\frac{1}{2}n \]

即：

\[b_n=b_{n-1}+\frac{1}{2}n^2-\frac{1}{2}n \]

其中，\(b_1=0\)。

再介绍下另一个比较常见的公式：

\[\sum_{i=1}^{n}i^2=\frac{1}{6}n(n+1)(2n+1) \]

那么对\(b_n\)的通项即可写作：

\[\frac{1}{2}\sum_{i=1}^{n}{i^2}-\frac{1}{4}n(n+1)\\ =\frac{1}{12}n(n+1)(2n+1)-\frac{1}{4}n(n+1)\\ =\frac{1}{6}n^3-\frac{1}{6}n \]

这里在引入另外一个式子：

\[\sum_{i=1}^{n}i^3=\frac{1}{4}n^4+\frac{1}{2}n^3+\frac{1}{4}n^2 \]

那么原式就可写成：

\[\sum_{i=1}^{n-2}b_i+\frac{n(n-1)}{2}+1\\ =\sum_{i=1}^{n-2}{[\frac{1}{6}i^3-\frac{1}{6}i]}+\frac{n(n-1)}{2}+1\\ =\frac{1}{6}\sum_{i=1}^{n-2}{i^3}-\frac{1}{6}\sum_{i=1}^{n-2}i+\frac{n(n-1)}{2}+1\\ \]

最终化简得到通项：

\[a_n=\frac{1}{24}(n^4-6n^3+23n^2-18n+24) \]

尝试验证第\(5，6\)项：

\[a_5=\frac{1}{24}(625-6\times125+23\times25-18\times5+24)=16\\ a_6=\frac{1}{24}(1296-6\times216+23\times36-18\times6+24)=31 \]

\(6\)个点的图长这样：

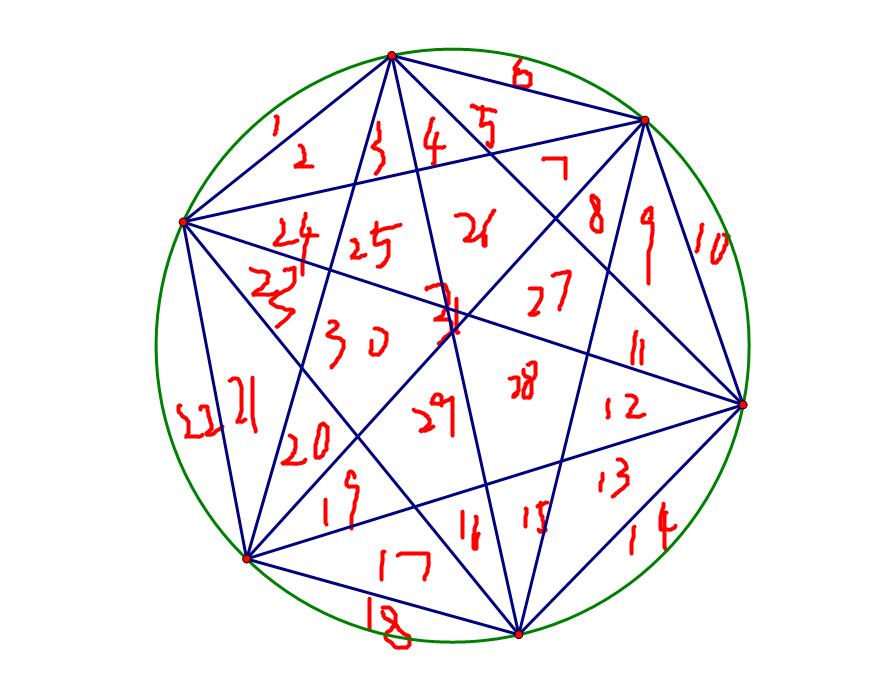
刚好\(31\)!

至此，推导完毕。