粒子群算法pso优化神经网络

参考：https://blog.csdn.net/a_hui_tai_lang/article/details/119877370

 

一个输入，一个输出的神经网络。只有两个可以训练的参数：w，b。没有中间层。

不用pso的情况下

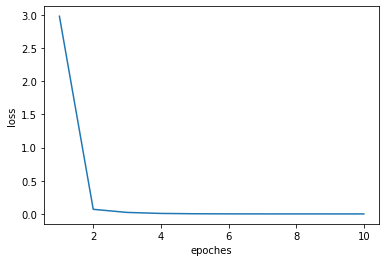
#导入包
import torch
import torch.nn as nn

#数据
data = torch.tensor([[[1],[2]],[[2],[4]],[[3],[6]],[[4],[8]],[[5],[10]]],dtype=torch.float)

#参数
epoches = 10
  

#搭建网络
class NNModel(torch.nn.Module):
    def __init__(self):
        
        super(NNModel,self).__init__()  #调用父类的初始化函数
        torch.manual_seed(50)           #设置随机数种子，防止预测的结果是随机数        
        self.layer1 = nn.Sequential(nn.Linear(1,1))

    def forward(self,mydata):
        mydata = self.layer1(mydata)

        return mydata


model = NNModel()                                      #实例化网络

criterion = nn.MSELoss()  
optimizer = torch.optim.SGD(model.parameters(), 0.1)   #设置优化函数和学习率
model.train()                                          #调整为训练模式
loss_list = []
for e in range(epoches):                               #训练网络      
    train_loss = 0                       
    for i in data:
        x = i[0]
        y = i[1]              
        #print(model.state_dict())                      #输出网络的权重参数  
        out = model(x)                                 #前向计算
        loss = criterion(out,y)                        #计算损失函数
        #print(loss)
        optimizer.zero_grad()
        loss.backward()                                #反向传播
        optimizer.step()
        train_loss += loss.item()
    loss_list.append(train_loss/len(data))

 
print(model.state_dict())
import matplotlib.pyplot as plt
loss_list = [float(i) for i in loss_list]
print(loss_list)
x = [i for i in range(1,len(loss_list)+1)]
plt.xlabel("epoches")
plt.ylabel("loss")
plt.plot(x,loss_list)

 

其loss随epoches的变化情况如下图所示

 

 

加了pso优化后的代码

#导入包
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
#数据
data = torch.tensor([[[1],[2]],[[2],[4]],[[3],[6]],[[4],[8]],[[5],[10]]],dtype=torch.float)

#参数
epoches = 10
import numpy as np
np.random.seed(1)
#搭建网络
class NNModel(torch.nn.Module):
    def __init__(self):
        
        super(NNModel,self).__init__()  #调用父类的初始化函数
        torch.manual_seed(50)           #设置随机数种子，防止预测的结果是随机数        
        self.layer1 = nn.Sequential(nn.Linear(1,1))

    def forward(self,mydata):
        mydata = self.layer1(mydata)

        return mydata


model = NNModel()                                      #实例化网络

criterion = nn.MSELoss()  
optimizer = torch.optim.SGD(model.parameters(), 0.1)   #设置优化函数和学习率
model.train()                                          #调整为训练模式

#粒子群优化模块
class Pso:
    def __init__(self,data,w,b):
        
        #先把输入从tensor变为numpy格式，w是1*1的二维，b是一维的
        self.data = data
        self.x = [np.array(i[0]) for i in data]
        self.y = [np.array(i[1]) for i in data]
        self.w = float(w)    #1*1
        self.b = float(b)    #1  1维
        #print(len(data),"数据长度")
        self.X = np.tile([self.w,self.b],(20,1))              #X是   种群数量*参数个数   


    def ooo(self):   #验证X确实是  数据长度*参数个数的维度   即5*1
        X = self.X
        return X
    

        
    def fitness_func(self,X):
        criterion = nn.MSELoss() 
        #每一组w和b都把所有的数据过一边，算出一个loss值
        #X是数据集长度*参数个数，就w和b，两个参数
        x = [float(i[0]) for i in self.data]
        y = [i[1] for i in self.data]
        
        
        x = np.array(x)
        #y = np.array(y)
        #print(X)
        loss_list = []
        #print("len(X)",len(X))
        for j in range(len(X)):   #粒子种群个数
            predict_y = []
            for i in range(len(y)):
                predict_y.append((X[j,0]*x+X[j,1]).astype(np.float64))
            #print(predict_y)
            #print(y)
            loss = criterion(torch.tensor(predict_y),torch.tensor(y))
            loss_list.append(loss)
            
        
        # w = X[:,0]
        # b = X[:,1]
        

        loss_list = np.array(loss_list)
        # print("------")
        # print(loss_list)
        # print("--------")
        return loss_list    #种群数量*1
    
    def velocity_update(self,V, X, pbest, gbest, c1, c2, w, max_val):    #更新速度
        """
        根据速度更新公式更新每个粒子的速度
        :param V: 粒子当前的速度矩阵，20*2 的矩阵
        :param X: 粒子当前的位置矩阵，20*2 的矩阵
        :param pbest: 每个粒子历史最优位置，20*2 的矩阵
        :param gbest: 种群历史最优位置，1*2 的矩阵
        """
        size = X.shape[0]
        r1 = np.random.random((size, 1))*0.01
        r2 = np.random.random((size, 1))*0.01
        V = w*V+c1*r1*(pbest-X)+c2*r2*(gbest-X)
        # 防止越界处理
        V[V < -max_val] = -max_val
        V[V > max_val] = max_val
        return V

    def position_update(self,X, V):
        """
        根据公式更新粒子的位置
        :param X: 粒子当前的位置矩阵，维度是 20*2
        :param V: 粒子当前的速度举着，维度是 20*2
        """
        return X+V
    def train(self,X):
        w = 1
        c1 = 1
        c2 = 1

        dim = 2
        size = 20         #size自己定，这是种群数量
        iter_num = 10000
        max_val = 0.5

        fitness_val_list = []
        # 初始化种群各个粒子的位置
        #X = np.random.uniform(-5, 5, size=(size, dim))   #X是神经网络训练完之后的权重，是一组权重和阈值的重复值
        X = X

        # 初始化各个粒子的速度
        V = np.random.uniform(-0.5, 0.5, size=(size, dim))
        #print(X)
        
        p_fitness = self.fitness_func(X)
        g_fitness = p_fitness.min()
        #print("最小的loss",g_fitness)
        fitness_val_list.append(g_fitness)
    
        # 初始化的个体最优位置和种群最优位置
        pbest = X
        gbest = X[p_fitness.argmin()]
        #print("整体最好的",gbest)
        # 迭代计算
        for i in range(1, iter_num):
            V = self.velocity_update(V, X, pbest, gbest, c1, c2, w, max_val)
            #print("V，X的更新量",V)
            X = self.position_update(X, V)
            p_fitness2 = self.fitness_func(X)
            g_fitness2 = p_fitness2.min()
    
            # 更新每个粒子的历史最优位置
            for j in range(size):
                if p_fitness[j] > p_fitness2[j]:
                    pbest[j] = X[j]
                    p_fitness[j] = p_fitness2[j]
                # 更新群体的最优位置
                if g_fitness > g_fitness2:
                    gbest = X[p_fitness2.argmin()]
                    g_fitness = g_fitness2
                # 记录最优迭代记录
                fitness_val_list.append(g_fitness)
                i += 1
            
        #print("优化完后整体最好的",gbest)
    
        # 输出迭代结果
        # print("最优值是：%.5f" % fitness_val_list[-1])
        # print("最优解是：x=%.5f,y=%.5f" % (gbest[0], gbest[1]))
    
        # 绘图
        # plt.plot(fitness_val_list, color='r')
        # plt.title('迭代过程')
        # plt.show()
        w = gbest[0]
        b = gbest[1]

        
        w = torch.tensor(w).reshape(1,1)
        b = torch.tensor(b).reshape(1)
        return w,b



loss_list = []
for e in range(epoches):                               #训练网络 
        #print(model.state_dict())
    train_loss = 0                       
    for i in data:
        x = i[0]
        y = i[1]              
        #print(model.state_dict())                      #输出网络的权重参数  
        out = model(x)                                 #前向计算
        loss = criterion(out,y)                        #计算损失函数
        #print(loss)
        optimizer.zero_grad()
        loss.backward()                                #反向传播
        optimizer.step()
        #print(model.state_dict())
        train_loss += loss.item()
    loss_list.append(train_loss/len(data))
    
    #粒子群优化
    #把当前的w和b提取出来
    w = model.state_dict()["layer1.0.weight"]  #1*1
    b = model.state_dict()['layer1.0.bias']    #1
    #print("pso之前",w,b)
    

    a = Pso(data,w,b) #Pso的输入和输出都是tensor
    X = a.ooo()
    # loss = a.fitness_func(X)
    # print(loss)
    new_w,new_b = a.train(X)
    #print("pso之后",new_w,new_b)

    model.state_dict()['layer1.0.weight'].copy_(new_w)
    model.state_dict()['layer1.0.bias'].copy_(new_b)

print(model.state_dict())
loss_list = [float(i) for i in loss_list]
#print(loss_list)
x = [i for i in range(1,len(loss_list)+1)]
plt.xlabel("epoches")
plt.ylabel("loss")
plt.plot(x,loss_list)

loss和epoches的相关曲线如下图

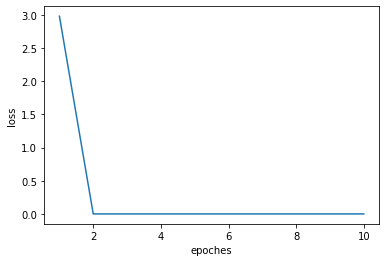
可能是网络比较简单的缘故，epoches下降的优化不是很明显