贝叶斯模型与Linux基本操作
贝叶斯模型
解释:
通过已知类别的训练数据集,计算样本的先验概率,然后利⽤⻉叶斯
概率公式测算未知类别样本属于某个类别的后验概率,
最终以最⼤后验概率所对应的类别作为样本的预测值。
贝叶斯分类器:
1.高斯贝叶斯分类器
适用于自变量为连续的数值类型的情况。
2.多项式贝叶斯分类器
适用于自变量为离散型类型的情况(可以理解为非数字类型)。
3.伯努利贝叶斯分类器
适用于自变量为二元值的情况。
贝叶斯代码实战:
皮肤案例:

# 导入第三方包 import pandas as pd # 读入数据 skin = pd.read_excel(r'Skin_Segment.xlsx') skin # 设置正例和负例 skin.y = skin.y.map({2:0,1:1}) # 设置一个映射关系,将2映射成0 skin.y.value_counts() skin # 导入第三方模块 from sklearn import model_selection # 样本拆分 X_train,X_test,y_train,y_test = model_selection.train_test_split(skin.iloc[:,:3], skin.y, test_size = 0.25, random_state=1234) # 导入第三方模块 from sklearn import naive_bayes # 调用高斯朴素贝叶斯分类器的“类” gnb = naive_bayes.GaussianNB() # 模型拟合 gnb.fit(X_train, y_train) # 模型在测试数据集上的预测 gnb_pred = gnb.predict(X_test) # 各类别的预测数量 pd.Series(gnb_pred).value_counts() # 导入第三方包 from sklearn import metrics import matplotlib.pyplot as plt import seaborn as sns # 构建混淆矩阵 cm = pd.crosstab(gnb_pred,y_test) # 绘制混淆矩阵图 sns.heatmap(cm, annot = True, cmap = 'GnBu', fmt = 'd') # 去除x轴和y轴标签 plt.xlabel('Real') plt.ylabel('Predict') # 显示图形 plt.show() print('模型的准确率为:\n',metrics.accuracy_score(y_test, gnb_pred)) print('模型的评估报告:\n',metrics.classification_report(y_test, gnb_pred)) # 计算正例的预测概率,用于生成ROC曲线的数据 y_score = gnb.predict_proba(X_test)[:,1] fpr,tpr,threshold = metrics.roc_curve(y_test, y_score) # 计算AUC的值 roc_auc = metrics.auc(fpr,tpr) # 绘制面积图 plt.stackplot(fpr, tpr, color='steelblue', alpha = 0.5, edgecolor = 'black') # 添加边际线 plt.plot(fpr, tpr, color='black', lw = 1) # 添加对角线 plt.plot([0,1],[0,1], color = 'red', linestyle = '--') # 添加文本信息 plt.text(0.5,0.3,'ROC curve (area = %0.2f)' % roc_auc) # 添加x轴与y轴标签 plt.xlabel('1-Specificity') plt.ylabel('Sensitivity') # 显示图形 plt.show()
评论案例:

import pandas as pd # 读入评论数据 evaluation = pd.read_excel(r'Contents.xlsx',sheet_name=0) # 查看数据前10行 evaluation.head(10) # 运用正则表达式,将评论中的数字和英文去除 evaluation.Content = evaluation.Content.str.replace('[0-9a-zA-Z]','') evaluation.head() # !pip3 install jieba !pip install jieba # 导入第三方包 import jieba # 加载自定义词库 jieba.load_userdict(r'all_words.txt') # 读入停止词 with open(r'mystopwords.txt', encoding='UTF-8') as words: stop_words = [i.strip() for i in words.readlines()] # 构造切词的自定义函数,并在切词过程中删除停止词 def cut_word(sentence): words = [i for i in jieba.lcut(sentence) if i not in stop_words] # 切完的词用空格隔开 result = ' '.join(words) return(result) # 对评论内容进行批量切词 words = evaluation.Content.apply(cut_word) # 前5行内容的切词效果 words[:5] # !pip3 install jieba # !pip install jieba # 导入第三方包 import jieba # 加载自定义词库 jieba.load_userdict(r'all_words.txt') # 读入停止词 with open(r'mystopwords.txt', encoding='UTF-8') as words: stop_words = [i.strip() for i in words.readlines()] # 构造切词的自定义函数,并在切词过程中删除停止词 def cut_word(sentence): words = [i for i in jieba.lcut(sentence) if i not in stop_words] # 切完的词用空格隔开 result = ' '.join(words) return(result) # 对评论内容进行批量切词 words = evaluation.Content.apply(cut_word) # 前5行内容的切词效果 words[:5] from sklearn import model_selection from sklearn import naive_bayes from sklearn import metrics import matplotlib.pyplot as plt import seaborn as sns # 将数据集拆分为训练集和测试集 X_train,X_test,y_train,y_test = model_selection.train_test_split(X,y,test_size = 0.25, random_state=1) # 构建伯努利贝叶斯分类器 bnb = naive_bayes.BernoulliNB() # 模型在训练数据集上的拟合 bnb.fit(X_train,y_train) # 模型在测试数据集上的预测 bnb_pred = bnb.predict(X_test) # 构建混淆矩阵 cm = pd.crosstab(bnb_pred,y_test) # 绘制混淆矩阵图 sns.heatmap(cm, annot = True, cmap = 'GnBu', fmt = 'd') # 去除x轴和y轴标签 plt.xlabel('Real') plt.ylabel('Predict') # 显示图形 plt.show() # 模型的预测准确率 print('模型的准确率为:\n',metrics.accuracy_score(y_test, bnb_pred)) print('模型的评估报告:\n',metrics.classification_report(y_test, bnb_pred)) # 计算正例Positive所对应的概率,用于生成ROC曲线的数据 y_score = bnb.predict_proba(X_test)[:,1] fpr,tpr,threshold = metrics.roc_curve(y_test.map({'Negative':0,'Positive':1}), y_score) # 计算AUC的值 roc_auc = metrics.auc(fpr,tpr) # 绘制面积图 plt.stackplot(fpr, tpr, color='steelblue', alpha = 0.5, edgecolor = 'black') # 添加边际线 plt.plot(fpr, tpr, color='black', lw = 1) # 添加对角线 plt.plot([0,1],[0,1], color = 'red', linestyle = '--') # 添加文本信息 plt.text(0.5,0.3,'ROC curve (area = %0.2f)' % roc_auc) # 添加x轴与y轴标签 plt.xlabel('1-Specificity') plt.ylabel('Sensitivity') # 显示图形 plt.show() # 计算正例Positive所对应的概率,用于生成ROC曲线的数据 y_score = bnb.predict_proba(X_test)[:,1] fpr,tpr,threshold = metrics.roc_curve(y_test.map({'Negative':0,'Positive':1}), y_score) # 计算AUC的值 roc_auc = metrics.auc(fpr,tpr) # 绘制面积图 plt.stackplot(fpr, tpr, color='steelblue', alpha = 0.5, edgecolor = 'black') # 添加边际线 plt.plot(fpr, tpr, color='black', lw = 1) # 添加对角线 plt.plot([0,1],[0,1], color = 'red', linestyle = '--') # 添加文本信息 plt.text(0.5,0.3,'ROC curve (area = %0.2f)' % roc_auc) # 添加x轴与y轴标签 plt.xlabel('1-Specificity') plt.ylabel('Sensitivity') # 显示图形 plt.show()
SVM模型
案例一:

# 导入第三方模块 from sklearn import svm import pandas as pd from sklearn import model_selection from sklearn import metrics # 读取外部数据 letters = pd.read_csv(r'letterdata.csv') # 数据前5行 letters.head() # 将数据拆分为训练集和测试集 predictors = letters.columns[1:] X_train,X_test,y_train,y_test = model_selection.train_test_split(letters[predictors], letters.letter, test_size = 0.25, random_state = 1234) # 选择线性可分SVM模型 linear_svc = svm.LinearSVC() # 模型在训练数据集上的拟合 linear_svc.fit(X_train,y_train) # 模型在测试集上的预测 pred_linear_svc = linear_svc.predict(X_test) # 模型的预测准确率 metrics.accuracy_score(y_test, pred_linear_svc) # 选择非线性SVM模型 nolinear_svc = svm.SVC(kernel='rbf') # 模型在训练数据集上的拟合 nolinear_svc.fit(X_train,y_train) # 模型在测试集上的预测 pred_svc = nolinear_svc.predict(X_test) # 模型的预测准确率 metrics.accuracy_score(y_test,pred_svc)
案例二:

# 读取外部数据 forestfires = pd.read_csv(r'forestfires.csv') # 数据前5行 forestfires.head() # 删除day变量 forestfires.drop('day',axis = 1, inplace = True) # 将月份作数值化处理 forestfires.month = pd.factorize(forestfires.month)[0] # 预览数据前5行 forestfires.head() # 导入第三方模块 import seaborn as sns import matplotlib.pyplot as plt from scipy.stats import norm # 绘制森林烧毁面积的直方图 sns.distplot(forestfires.area, bins = 50, kde = True, fit = norm, hist_kws = {'color':'steelblue'}, kde_kws = {'color':'red', 'label':'Kernel Density'}, fit_kws = {'color':'black','label':'Nomal', 'linestyle':'--'}) # 显示图例 plt.legend() # 显示图形 plt.show() # 导入第三方模块 from sklearn import preprocessing import numpy as np from sklearn import neighbors # 对area变量作对数变换 y = np.log1p(forestfires.area) # 将X变量作标准化处理 predictors = forestfires.columns[:-1] X = preprocessing.scale(forestfires[predictors]) # 将数据拆分为训练集和测试集 X_train,X_test,y_train,y_test = model_selection.train_test_split(X, y, test_size = 0.25, random_state = 1234) # 构建默认参数的SVM回归模型 svr = svm.SVR() # 模型在训练数据集上的拟合 svr.fit(X_train,y_train) # 模型在测试上的预测 pred_svr = svr.predict(X_test) # 计算模型的MSE metrics.mean_squared_error(y_test,pred_svr) # 使用网格搜索法,选择SVM回归中的最佳C值、epsilon值和gamma值 epsilon = np.arange(0.1,1.5,0.2) C= np.arange(100,1000,200) gamma = np.arange(0.001,0.01,0.002) parameters = {'epsilon':epsilon,'C':C,'gamma':gamma} grid_svr = model_selection.GridSearchCV(estimator = svm.SVR(max_iter=10000),param_grid =parameters, scoring='neg_mean_squared_error',cv=5,verbose =1, n_jobs=2) # 模型在训练数据集上的拟合 grid_svr.fit(X_train,y_train) # 返回交叉验证后的最佳参数值 print(grid_svr.best_params_, grid_svr.best_score_) # 模型在测试集上的预测 pred_grid_svr = grid_svr.predict(X_test) # 计算模型在测试集上的MSE值 metrics.mean_squared_error(y_test,pred_grid_svr)
超平面的概念(一维、二维、三维)
# 将样本点分成不同的类别(三种表现形式:点、线、面)
超平面最优解
# 1.先随机选择一条直线 # 2.分别计算两边距离到该直线最短的距离 取最小的距离 # 3.以该距离左右两边做分隔带 # 4.依次执行上述三个步骤得出N多个分隔带 最优解的就是分割带最宽的
线性可风与非线性可分
# 线性可分:简单的理解就是一条直线划分类别 # 非线性可分:一条直线无法直接划分 需要升一个维度在做划分 # 补充:高斯核函数>>>:支持无穷维
K均值聚类
案例一:

# 导入第三方包 import pandas as pd import numpy as np import matplotlib.pyplot as plt from sklearn.cluster import KMeans from sklearn import metrics # 随机生成三组二元正态分布随机数 np.random.seed(1234) mean1 = [0.5, 0.5] cov1 = [[0.3, 0], [0, 0.3]] x1, y1 = np.random.multivariate_normal(mean1, cov1, 1000).T mean2 = [0, 8] cov2 = [[1.5, 0], [0, 1]] x2, y2 = np.random.multivariate_normal(mean2, cov2, 1000).T mean3 = [8, 4] cov3 = [[1.5, 0], [0, 1]] x3, y3 = np.random.multivariate_normal(mean3, cov3, 1000).T # 绘制三组数据的散点图 plt.scatter(x1,y1) plt.scatter(x2,y2) plt.scatter(x3,y3) # 显示图形 plt.show() # 构造自定义函数,用于绘制不同k值和对应总的簇内离差平方和的折线图 def k_SSE(X, clusters): # 选择连续的K种不同的值 K = range(1,clusters+1) # 构建空列表用于存储总的簇内离差平方和 TSSE = [] for k in K: # 用于存储各个簇内离差平方和 SSE = [] kmeans = KMeans(n_clusters=k) kmeans.fit(X) # 返回簇标签 labels = kmeans.labels_ # 返回簇中心 centers = kmeans.cluster_centers_ # 计算各簇样本的离差平方和,并保存到列表中 for label in set(labels): SSE.append(np.sum((X.loc[labels == label,]-centers[label,:])**2)) # 计算总的簇内离差平方和 TSSE.append(np.sum(SSE)) # 中文和负号的正常显示 plt.rcParams['font.sans-serif'] = ['Microsoft YaHei'] plt.rcParams['axes.unicode_minus'] = False # 设置绘图风格 plt.style.use('ggplot') # 绘制K的个数与GSSE的关系 plt.plot(K, TSSE, 'b*-') plt.xlabel('簇的个数') plt.ylabel('簇内离差平方和之和') # 显示图形 plt.show() # 将三组数据集汇总到数据框中 X = pd.DataFrame(np.concatenate([np.array([x1,y1]),np.array([x2,y2]),np.array([x3,y3])], axis = 1).T) # 自定义函数的调用 k_SSE(X, 15) # 构造自定义函数,用于绘制不同k值和对应轮廓系数的折线图 def k_silhouette(X, clusters): K = range(2,clusters+1) # 构建空列表,用于存储个中簇数下的轮廓系数 S = [] for k in K: kmeans = KMeans(n_clusters=k) kmeans.fit(X) labels = kmeans.labels_ # 调用字模块metrics中的silhouette_score函数,计算轮廓系数 S.append(metrics.silhouette_score(X, labels, metric='euclidean')) # 中文和负号的正常显示 plt.rcParams['font.sans-serif'] = ['Microsoft YaHei'] plt.rcParams['axes.unicode_minus'] = False # 设置绘图风格 plt.style.use('ggplot') # 绘制K的个数与轮廓系数的关系 plt.plot(K, S, 'b*-') plt.xlabel('簇的个数') plt.ylabel('轮廓系数') # 显示图形 plt.show() # 自定义函数的调用 k_silhouette(X, 15)
案例二:

# 读取iris数据集 iris = pd.read_csv(r'iris.csv') # 查看数据集的前几行 iris.head() # 提取出用于建模的数据集X X = iris.drop(labels = 'Species', axis = 1) # 构建Kmeans模型 kmeans = KMeans(n_clusters = 3) kmeans.fit(X) # 聚类结果标签 X['cluster'] = kmeans.labels_ # 各类频数统计 X.cluster.value_counts() # 导入第三方模块 import seaborn as sns # 三个簇的簇中心 centers = kmeans.cluster_centers_ # 绘制聚类效果的散点图 sns.lmplot(x = 'Petal_Length', y = 'Petal_Width', hue = 'cluster', markers = ['^','s','o'], data = X, fit_reg = False, scatter_kws = {'alpha':0.8}, legend_out = False) plt.scatter(centers[:,2], centers[:,3], marker = '*', color = 'black', s = 130) plt.xlabel('花瓣长度') plt.ylabel('花瓣宽度') # 图形显示 plt.show() # 增加一个辅助列,将不同的花种映射到0,1,2三种值,目的方便后面图形的对比 iris['Species_map'] = iris.Species.map({'virginica':0,'setosa':1,'versicolor':2}) # 绘制原始数据三个类别的散点图 sns.lmplot(x = 'Petal_Length', y = 'Petal_Width', hue = 'Species_map', data = iris, markers = ['^','s','o'], fit_reg = False, scatter_kws = {'alpha':0.8}, legend_out = False) plt.xlabel('花瓣长度') plt.ylabel('花瓣宽度') # 图形显示 plt.show() # 读取球员数据 players = pd.read_csv(r'players.csv') players.head() # 绘制得分与命中率的散点图 sns.lmplot(x = '得分', y = '命中率', data = players, fit_reg = False, scatter_kws = {'alpha':0.8, 'color': 'steelblue'}) plt.show() from sklearn import preprocessing # 数据标准化处理 X = preprocessing.minmax_scale(players[['得分','罚球命中率','命中率','三分命中率']]) # 将数组转换为数据框 X = pd.DataFrame(X, columns=['得分','罚球命中率','命中率','三分命中率']) # 使用拐点法选择最佳的K值 k_SSE(X, 15) # 使用轮廓系数选择最佳的K值 k_silhouette(X, 10) # 将球员数据集聚为3类 kmeans = KMeans(n_clusters = 3) kmeans.fit(X) # 将聚类结果标签插入到数据集players中 players['cluster'] = kmeans.labels_ # 构建空列表,用于存储三个簇的簇中心 centers = [] for i in players.cluster.unique(): centers.append(players.ix[players.cluster == i,['得分','罚球命中率','命中率','三分命中率']].mean()) # 将列表转换为数组,便于后面的索引取数 centers = np.array(centers) # 绘制散点图 sns.lmplot(x = '得分', y = '命中率', hue = 'cluster', data = players, markers = ['^','s','o'], fit_reg = False, scatter_kws = {'alpha':0.8}, legend = False) # 添加簇中心 plt.scatter(centers[:,0], centers[:,2], c='k', marker = '*', s = 180) plt.xlabel('得分') plt.ylabel('命中率') # 图形显示 plt.show()
K值的求解(K表示分成几类)
1.拐点法
计算不同K值下类别中离差平方和(看斜率 变化越明显越好)。
2.轮廓系数法
计算轮廓系数(看大小 越大越好)。
DBSCAN(密度)聚类
案例一:

# 导入第三方模块 import pandas as pd import numpy as np from sklearn.datasets.samples_generator import make_blobs import matplotlib.pyplot as plt import seaborn as sns from sklearn import cluster # 模拟数据集 X,y = make_blobs(n_samples = 2000, centers = [[-1,-2],[1,3]], cluster_std = [0.5,0.5], random_state = 1234) # 将模拟得到的数组转换为数据框,用于绘图 plot_data = pd.DataFrame(np.column_stack((X,y)), columns = ['x1','x2','y']) # 设置绘图风格 plt.style.use('ggplot') # 绘制散点图(用不同的形状代表不同的簇) sns.lmplot('x1', 'x2', data = plot_data, hue = 'y',markers = ['^','o'], fit_reg = False, legend = False) # 显示图形 plt.show() # 导入第三方模块 from sklearn import cluster # 构建Kmeans聚类和密度聚类 kmeans = cluster.KMeans(n_clusters=2, random_state=1234) kmeans.fit(X) dbscan = cluster.DBSCAN(eps = 0.5, min_samples = 10) dbscan.fit(X) # 将Kmeans聚类和密度聚类的簇标签添加到数据框中 plot_data['kmeans_label'] = kmeans.labels_ plot_data['dbscan_label'] = dbscan.labels_ # 绘制聚类效果图 # 设置大图框的长和高 plt.figure(figsize = (12,6)) # 设置第一个子图的布局 ax1 = plt.subplot2grid(shape = (1,2), loc = (0,0)) # 绘制散点图 ax1.scatter(plot_data.x1, plot_data.x2, c = plot_data.kmeans_label) # 设置第二个子图的布局 ax2 = plt.subplot2grid(shape = (1,2), loc = (0,1)) # 绘制散点图(为了使Kmeans聚类和密度聚类的效果图颜色一致,通过序列的map“方法”对颜色作重映射) ax2.scatter(plot_data.x1, plot_data.x2, c=plot_data.dbscan_label.map({-1:1,0:2,1:0})) # 显示图形 plt.show() # 导入第三方模块 from sklearn.datasets.samples_generator import make_moons # 构造非球形样本点 X1,y1 = make_moons(n_samples=2000, noise = 0.05, random_state = 1234) # 构造球形样本点 X2,y2 = make_blobs(n_samples=1000, centers = [[3,3]], cluster_std = 0.5, random_state = 1234) # 将y2的值替换为2(为了避免与y1的值冲突,因为原始y1和y2中都有0这个值) y2 = np.where(y2 == 0,2,0) # 将模拟得到的数组转换为数据框,用于绘图 plot_data = pd.DataFrame(np.row_stack([np.column_stack((X1,y1)),np.column_stack((X2,y2))]), columns = ['x1','x2','y']) # 绘制散点图(用不同的形状代表不同的簇) sns.lmplot('x1', 'x2', data = plot_data, hue = 'y',markers = ['^','o','>'], fit_reg = False, legend = False) # 显示图形 plt.show() # 构建Kmeans聚类和密度聚类 kmeans = cluster.KMeans(n_clusters=3, random_state=1234) kmeans.fit(plot_data[['x1','x2']]) dbscan = cluster.DBSCAN(eps = 0.3, min_samples = 5) dbscan.fit(plot_data[['x1','x2']]) # 将Kmeans聚类和密度聚类的簇标签添加到数据框中 plot_data['kmeans_label'] = kmeans.labels_ plot_data['dbscan_label'] = dbscan.labels_ # 绘制聚类效果图 # 设置大图框的长和高 plt.figure(figsize = (12,6)) # 设置第一个子图的布局 ax1 = plt.subplot2grid(shape = (1,2), loc = (0,0)) # 绘制散点图 ax1.scatter(plot_data.x1, plot_data.x2, c = plot_data.kmeans_label) # 设置第二个子图的布局 ax2 = plt.subplot2grid(shape = (1,2), loc = (0,1)) # 绘制散点图(为了使Kmeans聚类和密度聚类的效果图颜色一致,通过序列的map“方法”对颜色作重映射) ax2.scatter(plot_data.x1, plot_data.x2, c=plot_data.dbscan_label.map({-1:1,0:0,1:3,2:2})) # 显示图形 plt.show()
案例二:

# 读取外部数据 Province = pd.read_excel(r'Province.xlsx') Province.head() # 绘制出生率与死亡率散点图 plt.scatter(Province.Birth_Rate, Province.Death_Rate, c = 'steelblue') # 添加轴标签 plt.xlabel('Birth_Rate') plt.ylabel('Death_Rate') # 显示图形 plt.show() # 读入第三方包 from sklearn import preprocessing # 选取建模的变量 predictors = ['Birth_Rate','Death_Rate'] # 变量的标准化处理 X = preprocessing.scale(Province[predictors]) X = pd.DataFrame(X) X # 构建空列表,用于保存不同参数组合下的结果 res = [] # 迭代不同的eps值 for eps in np.arange(0.001,1,0.05): # 迭代不同的min_samples值 for min_samples in range(2,10): dbscan = cluster.DBSCAN(eps = eps, min_samples = min_samples) # 模型拟合 dbscan.fit(X) # 统计各参数组合下的聚类个数(-1表示异常点) n_clusters = len([i for i in set(dbscan.labels_) if i != -1]) # 异常点的个数 outliners = np.sum(np.where(dbscan.labels_ == -1, 1,0)) # 统计每个簇的样本个数 stats = str(pd.Series([i for i in dbscan.labels_ if i != -1]).value_counts().values) res.append({'eps':eps,'min_samples':min_samples,'n_clusters':n_clusters,'outliners':outliners,'stats':stats}) # 将迭代后的结果存储到数据框中 df = pd.DataFrame(res) df # 根据条件筛选合理的参数组合 df.loc[df.n_clusters == 3, :] %matplotlib # 中文乱码和坐标轴负号的处理 plt.rcParams['font.sans-serif'] = ['Microsoft YaHei'] plt.rcParams['axes.unicode_minus'] = False # 利用上述的参数组合值,重建密度聚类算法 dbscan = cluster.DBSCAN(eps = 0.801, min_samples = 3) # 模型拟合 dbscan.fit(X) Province['dbscan_label'] = dbscan.labels_ # 绘制聚类聚类的效果散点图 sns.lmplot(x = 'Birth_Rate', y = 'Death_Rate', hue = 'dbscan_label', data = Province, markers = ['*','d','^','o'], fit_reg = False, legend = False) # 添加省份标签 for x,y,text in zip(Province.Birth_Rate,Province.Death_Rate, Province.Province): plt.text(x+0.1,y-0.1,text, size = 8) # 添加参考线 plt.hlines(y = 5.8, xmin = Province.Birth_Rate.min(), xmax = Province.Birth_Rate.max(), linestyles = '--', colors = 'red') plt.vlines(x = 10, ymin = Province.Death_Rate.min(), ymax = Province.Death_Rate.max(), linestyles = '--', colors = 'red') # 添加轴标签 plt.xlabel('Birth_Rate') plt.ylabel('Death_Rate') # 显示图形 plt.show() # 导入第三方模块 from sklearn import metrics # 构造自定义函数,用于绘制不同k值和对应轮廓系数的折线图 def k_silhouette(X, clusters): K = range(2,clusters+1) # 构建空列表,用于存储个中簇数下的轮廓系数 S = [] for k in K: kmeans = cluster.KMeans(n_clusters=k) kmeans.fit(X) labels = kmeans.labels_ # 调用字模块metrics中的silhouette_score函数,计算轮廓系数 S.append(metrics.silhouette_score(X, labels, metric='euclidean')) # 中文和负号的正常显示 plt.rcParams['font.sans-serif'] = ['Microsoft YaHei'] plt.rcParams['axes.unicode_minus'] = False # 设置绘图风格 plt.style.use('ggplot') # 绘制K的个数与轮廓系数的关系 plt.plot(K, S, 'b*-') plt.xlabel('簇的个数') plt.ylabel('轮廓系数') # 显示图形 plt.show() # 聚类个数的探索 k_silhouette(X, clusters = 10) # 利用Kmeans聚类 kmeans = cluster.KMeans(n_clusters = 3) # 模型拟合 kmeans.fit(X) Province['kmeans_label'] = kmeans.labels_ # 绘制Kmeans聚类的效果散点图 sns.lmplot(x = 'Birth_Rate', y = 'Death_Rate', hue = 'kmeans_label', data = Province, markers = ['d','^','o'], fit_reg = False, legend = False) # 添加轴标签 plt.xlabel('Birth_Rate') plt.ylabel('Death_Rate') plt.show()
K均值聚类的两大缺点:
1.聚类效果容易受到异常样本点的影响。
2.无法准确的将非球形样本进行合理的聚类。
所以可以采用密度聚类来解决上述两个问题
DBSCAN聚类核心概念
核心对象:内部含有至少大于等于最少样本点的样本。
非核心对象:内部少于最少样本点的样本。
直接密度可达:在核心对象的内部样本点到核心对象的距离。
密度可达:多个直接密度可达链接了多个核心对象(首尾点密度可达)。
密度相连:两边的点由中间的核心对象分别为密度可达,那么这两个点称为密度相连。
GBDT模型
Adaboost算法(既可以解决分类问题也可以解决预测问题)
由多颗基础决策树组成 并且这些决策树彼此之间有先后关系
SMOTE算法
通过算法将比例较少的数据样本扩大
案例一:

# 导入第三方包 import pandas as pd import matplotlib.pyplot as plt # 读入数据 default = pd.read_excel(r'default of credit card.xls') # 数据集中是否违约的客户比例 plt.rcParams['font.sans-serif'] = ['Microsoft YaHei'] plt.rcParams['axes.unicode_minus'] = False # 统计客户是否违约的频数 counts = default.y.value_counts() # 绘制饼图 plt.pie(x = counts, # 绘图数据 labels=pd.Series(counts.index).map({0:'不违约',1:'违约'}), # 添加文字标签 autopct='%.1f%%' # 设置百分比的格式,这里保留一位小数 ) # 显示图形 plt.show() # 将数据集拆分为训练集和测试集 # 导入第三方包 from sklearn import model_selection from sklearn import ensemble from sklearn import metrics # 排除数据集中的ID变量和因变量,剩余的数据用作自变量X X = default.drop(['ID','y'], axis = 1) y = default.y # 数据拆分 X_train,X_test,y_train,y_test = model_selection.train_test_split(X,y,test_size = 0.25, random_state = 1234) # 构建AdaBoost算法的类 AdaBoost1 = ensemble.AdaBoostClassifier() # 算法在训练数据集上的拟合 AdaBoost1.fit(X_train,y_train) # 算法在测试数据集上的预测 pred1 = AdaBoost1.predict(X_test) # 返回模型的预测效果 print('模型的准确率为:\n',metrics.accuracy_score(y_test, pred1)) print('模型的评估报告:\n',metrics.classification_report(y_test, pred1)) # 计算客户违约的概率值,用于生成ROC曲线的数据 y_score = AdaBoost1.predict_proba(X_test)[:,1] fpr,tpr,threshold = metrics.roc_curve(y_test, y_score) # 计算AUC的值 roc_auc = metrics.auc(fpr,tpr) # 绘制面积图 plt.stackplot(fpr, tpr, color='steelblue', alpha = 0.5, edgecolor = 'black') # 添加边际线 plt.plot(fpr, tpr, color='black', lw = 1) # 添加对角线 plt.plot([0,1],[0,1], color = 'red', linestyle = '--') # 添加文本信息 plt.text(0.5,0.3,'ROC curve (area = %0.2f)' % roc_auc) # 添加x轴与y轴标签 plt.xlabel('1-Specificity') plt.ylabel('Sensitivity') # 显示图形 plt.show() # 自变量的重要性排序 importance = pd.Series(AdaBoost1.feature_importances_, index = X.columns) importance.sort_values().plot(kind = 'barh') plt.show() # 取出重要性比较高的自变量建模 predictors = list(importance[importance>0.02].index) predictors # 通过网格搜索法选择基础模型所对应的合理参数组合 # 导入第三方包 from sklearn.model_selection import GridSearchCV from sklearn.tree import DecisionTreeClassifier max_depth = [3,4,5,6] params1 = {'base_estimator__max_depth':max_depth} base_model = GridSearchCV(estimator = ensemble.AdaBoostClassifier(base_estimator = DecisionTreeClassifier()), param_grid= params1, scoring = 'roc_auc', cv = 5, n_jobs = 4, verbose = 1) base_model.fit(X_train[predictors],y_train) # 返回参数的最佳组合和对应AUC值 base_model.best_params_, base_model.best_score_ # 通过网格搜索法选择提升树的合理参数组合 # 导入第三方包 from sklearn.model_selection import GridSearchCV n_estimators = [100,200,300] learning_rate = [0.01,0.05,0.1,0.2] params2 = {'n_estimators':n_estimators,'learning_rate':learning_rate} adaboost = GridSearchCV(estimator = ensemble.AdaBoostClassifier(base_estimator = DecisionTreeClassifier(max_depth = 3)), param_grid= params2, scoring = 'roc_auc', cv = 5, n_jobs = 4, verbose = 1) adaboost.fit(X_train[predictors] ,y_train) # 返回参数的最佳组合和对应AUC值 adaboost.best_params_, adaboost.best_score_ # 使用最佳的参数组合构建AdaBoost模型 AdaBoost2 = ensemble.AdaBoostClassifier(base_estimator = DecisionTreeClassifier(max_depth = 3), n_estimators = 300, learning_rate = 0.01) # 算法在训练数据集上的拟合 AdaBoost2.fit(X_train[predictors],y_train) # 算法在测试数据集上的预测 pred2 = AdaBoost2.predict(X_test[predictors]) # 返回模型的预测效果 print('模型的准确率为:\n',metrics.accuracy_score(y_test, pred2)) print('模型的评估报告:\n',metrics.classification_report(y_test, pred2)) # 计算正例的预测概率,用于生成ROC曲线的数据 y_score = AdaBoost2.predict_proba(X_test[predictors])[:,1] fpr,tpr,threshold = metrics.roc_curve(y_test, y_score) # 计算AUC的值 roc_auc = metrics.auc(fpr,tpr) # 绘制面积图 plt.stackplot(fpr, tpr, color='steelblue', alpha = 0.5, edgecolor = 'black') # 添加边际线 plt.plot(fpr, tpr, color='black', lw = 1) # 添加对角线 plt.plot([0,1],[0,1], color = 'red', linestyle = '--') # 添加文本信息 plt.text(0.5,0.3,'ROC curve (area = %0.2f)' % roc_auc) # 添加x轴与y轴标签 plt.xlabel('1-Specificity') plt.ylabel('Sensitivity') # 显示图形 plt.show()
案例二:

# 运用网格搜索法选择梯度提升树的合理参数组合 learning_rate = [0.01,0.05,0.1,0.2] n_estimators = [100,300,500] max_depth = [3,4,5,6] params = {'learning_rate':learning_rate,'n_estimators':n_estimators,'max_depth':max_depth} gbdt_grid = GridSearchCV(estimator = ensemble.GradientBoostingClassifier(), param_grid= params, scoring = 'roc_auc', cv = 5, n_jobs = 4, verbose = 1) gbdt_grid.fit(X_train[predictors],y_train) # 返回参数的最佳组合和对应AUC值 gbdt_grid.best_params_, gbdt_grid.best_score_ # 基于最佳参数组合的GBDT模型,对测试数据集进行预测 pred = gbdt_grid.predict(X_test[predictors]) # 返回模型的预测效果 print('模型的准确率为:\n',metrics.accuracy_score(y_test, pred)) print('模型的评估报告:\n',metrics.classification_report(y_test, pred)) # 计算违约客户的概率值,用于生成ROC曲线的数据 y_score = gbdt_grid.predict_proba(X_test[predictors])[:,1] fpr,tpr,threshold = metrics.roc_curve(y_test, y_score) # 计算AUC的值 roc_auc = metrics.auc(fpr,tpr) # 绘制面积图 plt.stackplot(fpr, tpr, color='steelblue', alpha = 0.5, edgecolor = 'black') # 添加边际线 plt.plot(fpr, tpr, color='black', lw = 1) # 添加对角线 plt.plot([0,1],[0,1], color = 'red', linestyle = '--') # 添加文本信息 plt.text(0.5,0.3,'ROC curve (area = %0.2f)' % roc_auc) # 添加x轴与y轴标签 plt.xlabel('1-Specificity') plt.ylabel('Sensitivity') # 显示图形 plt.show() # 读入数据 creditcard = pd.read_csv(r'creditcard.csv') # 为确保绘制的饼图为圆形,需执行如下代码 plt.axes(aspect = 'equal') # 统计交易是否为欺诈的频数 counts = creditcard.Class.value_counts() # 绘制饼图 plt.pie(x = counts, # 绘图数据 labels=pd.Series(counts.index).map({0:'正常',1:'欺诈'}), # 添加文字标签 autopct='%.2f%%' # 设置百分比的格式,这里保留一位小数 ) # 显示图形 plt.show() # 将数据拆分为训练集和测试集 # 删除自变量中的Time变量 X = creditcard.drop(['Time','Class'], axis = 1) y = creditcard.Class # 数据拆分 X_train,X_test,y_train,y_test = model_selection.train_test_split(X,y,test_size = 0.3, random_state = 1234) !pip3 install imblearn # 导入第三方包 from imblearn.over_sampling import SMOTE # 运用SMOTE算法实现训练数据集的平衡 over_samples = SMOTE(random_state=1234) # over_samples_X,over_samples_y = over_samples.fit_sample(X_train, y_train) over_samples_X, over_samples_y = over_samples.fit_sample(X_train.values,y_train.values.ravel()) # 重抽样前的类别比例 print(y_train.value_counts()/len(y_train)) # 重抽样后的类别比例 print(pd.Series(over_samples_y).value_counts()/len(over_samples_y)) # https://www.lfd.uci.edu/~gohlke/pythonlibs/ # 导入第三方包 import xgboost import numpy as np # 构建XGBoost分类器 xgboost = xgboost.XGBClassifier() # 使用重抽样后的数据,对其建模 xgboost.fit(over_samples_X,over_samples_y) # 将模型运用到测试数据集中 resample_pred = xgboost.predict(np.array(X_test)) # 返回模型的预测效果 print('模型的准确率为:\n',metrics.accuracy_score(y_test, resample_pred)) print('模型的评估报告:\n',metrics.classification_report(y_test, resample_pred)) # 计算欺诈交易的概率值,用于生成ROC曲线的数据 y_score = xgboost.predict_proba(np.array(X_test))[:,1] fpr,tpr,threshold = metrics.roc_curve(y_test, y_score) # 计算AUC的值 roc_auc = metrics.auc(fpr,tpr) # 绘制面积图 plt.stackplot(fpr, tpr, color='steelblue', alpha = 0.5, edgecolor = 'black') # 添加边际线 plt.plot(fpr, tpr, color='black', lw = 1) # 添加对角线 plt.plot([0,1],[0,1], color = 'red', linestyle = '--') # 添加文本信息 plt.text(0.5,0.3,'ROC curve (area = %0.2f)' % roc_auc) # 添加x轴与y轴标签 plt.xlabel('1-Specificity') plt.ylabel('Sensitivity') # 显示图形 plt.show() # 构建XGBoost分类器 import xgboost xgboost2 = xgboost.XGBClassifier() # 使用非平衡的训练数据集拟合模型 xgboost2.fit(X_train,y_train) # 基于拟合的模型对测试数据集进行预测 pred2 = xgboost2.predict(X_test) # 混淆矩阵 pd.crosstab(pred2,y_test) # 返回模型的预测效果 print('模型的准确率为:\n',metrics.accuracy_score(y_test, pred2)) print('模型的评估报告:\n',metrics.classification_report(y_test, pred2)) # 计算欺诈交易的概率值,用于生成ROC曲线的数据 y_score = xgboost2.predict_proba(X_test)[:,1] fpr,tpr,threshold = metrics.roc_curve(y_test, y_score) # 计算AUC的值 roc_auc = metrics.auc(fpr,tpr) # 绘制面积图 plt.stackplot(fpr, tpr, color='steelblue', alpha = 0.5, edgecolor = 'black') # 添加边际线 plt.plot(fpr, tpr, color='black', lw = 1) # 添加对角线 plt.plot([0,1],[0,1], color = 'red', linestyle = '--') # 添加文本信息 plt.text(0.5,0.3,'ROC curve (area = %0.2f)' % roc_auc) # 添加x轴与y轴标签 plt.xlabel('1-Specificity') plt.ylabel('Sensitivity') # 显示图形 plt.show()
Linux前期知识(操作)
电脑的种类
-
-
笔记本
-
作用: 1.可以尽量避免数据不会丢失 2.可以24小时不间断提供服务 3.可以提升用户体验 ps:运维人员的工作,本质上就是为了上述三点的实现
服务器的种类
戴尔dell(常见) 华为 IBM(被联想收购更名为thinkserver) 浪潮(国内居多) ... """ 服务器尺寸描述主要以U为单位 1U=1.75英寸=4.445CM=4.45CM 常见服务器尺寸 1U 2U 4U """
电源 主板 CPU 内存 硬盘 散热系统 工作原理 1) 电源: 冗余技术: UPS(不间断电源系统)、双路或多路供电、发电机 2) CPU: 做数据运算处理 CPU路数 单路==1个 双路==2个 四路==4个 CPU核数 把CPU比喻成厂房, 将CPU中的核数比喻成厂房中的工人, CPU核数是真正处理工作任务,CPU核数越多, 同时处理工作任务的效率越高 3) 内存: 临时存储数据(断电数据即丢失) 程序 进程(存储在内存中) 守护进程 代码 运行起来的程序 根本停不下来的进程 缓存cache 缓冲buffer 内存存储空间一分为二(公交车上下车位置) cache缓存 从缓存读数据 buffer缓冲 从缓冲写数据 企业案例: 高并发存储数据环境 存: 将数据先存储到内存 在存储到磁盘中 读: 将磁盘中的热点数据存储到内存中 低并发存储数据环境 存: 将数据先放到硬盘里 读: 将磁盘中的热点数据存储到内存中 4) 硬盘: 永久存储数据(断电数据不会丢失) 硬盘种类: 机械硬盘(性能低) 固态硬盘(性能高) 硬盘接口(茶壶壶嘴):SATA< SCSI <SAS <PCI-E 服务器磁盘阵列(raid) 1)服务器上有多块硬盘保证数据不容易丢失 2)服务器上存储数据较多可以将多块硬盘进行整合 3)服务器上存储大容量数据效率更高 服务器磁盘阵列(raid) 见下图 按照不同级别进行多块硬盘整合 2块(raid0 raid1) 3块(raid5) 4块(raid01 raid10) raid0 :存储量-没有浪费 优势:提升数据存储效率 缺点:容易丢失数据 raid1:存储量-浪费一半 优势:不容易丢失数据,数据更加安全 缺点:数据存储效率较低 raid5:(至少需要3块硬盘)存储量--损失一块盘容量 优势:安全 存储数据性能也比较高 缺点:最多只能坏一块盘 5)远程管理卡 远程控制管理服务器的运行状态 远程安装操作系统 远程配置raid阵列信息 PS:一定要确认远程管理卡的默认地址信息 6)光驱(安装系统)-- 淘汰 U盘安装系统 kickstart cobbler -- 无人值守安装系统 7)机柜 机柜里面线缆一定要布线整齐 设置标签
虚拟化
存储知识
什么是虚拟化?
将一台计算机硬件"拆分"成多份分配使用。
如何实现虚拟化
vmware软件
vmware12 支持windows64
vmware8 支持windows32
vmware fusion 支持苹果系统
VMware12
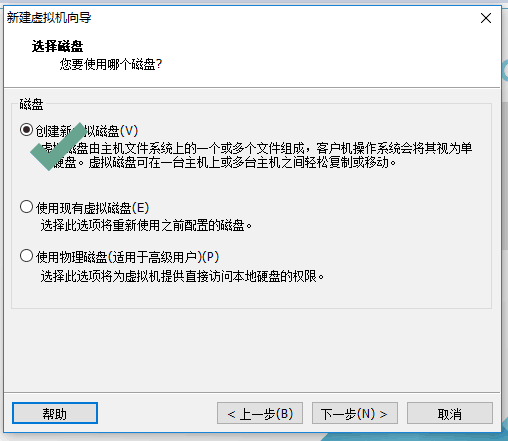
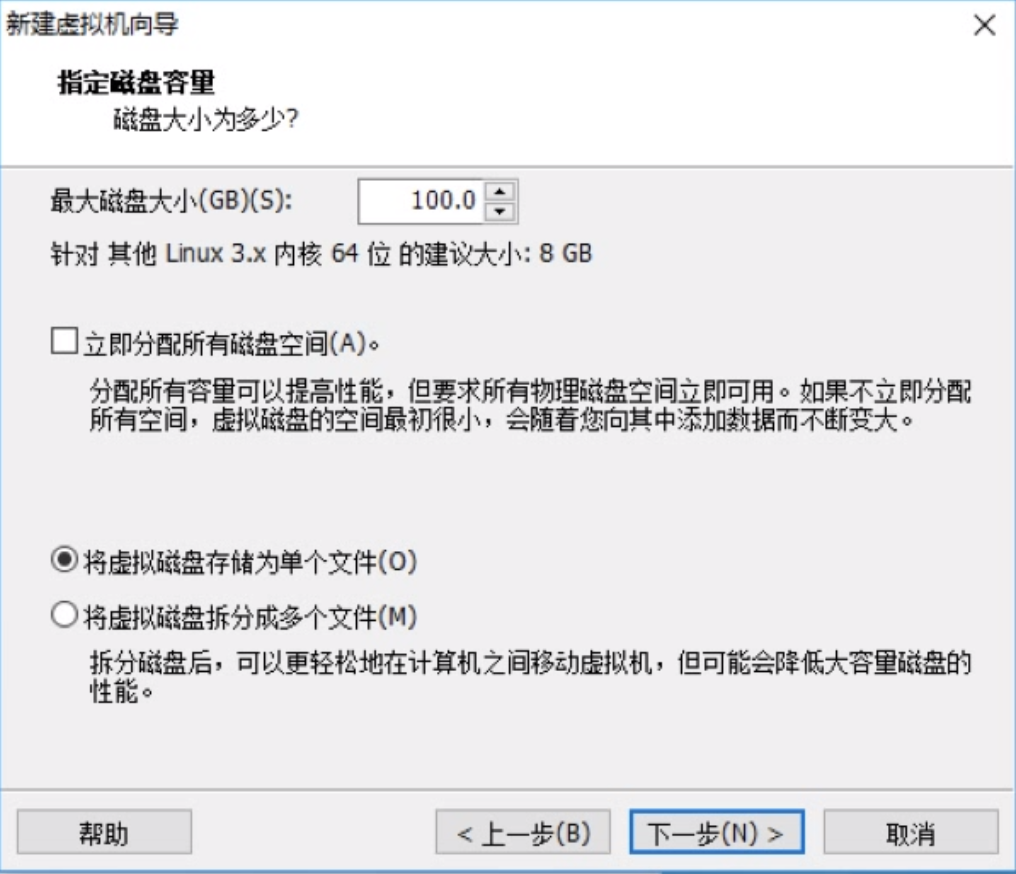
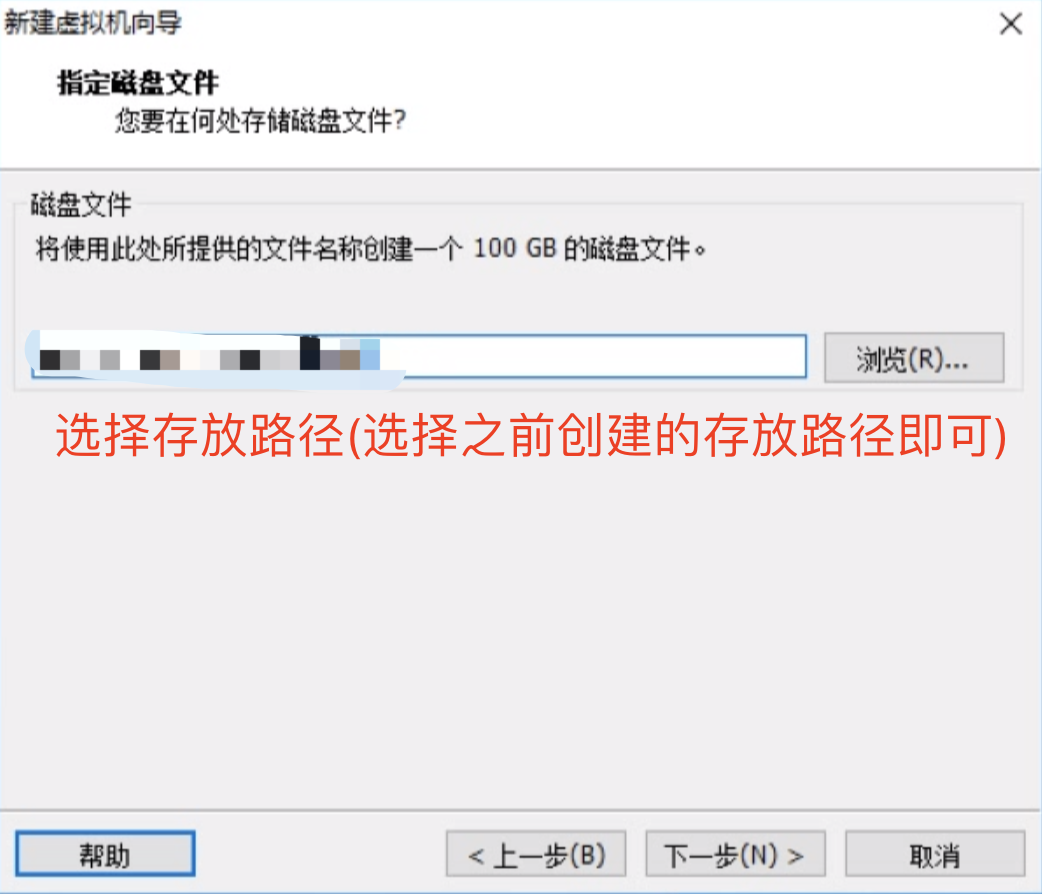
接着我们要创建虚拟机了,参考下面的详细图示即可。
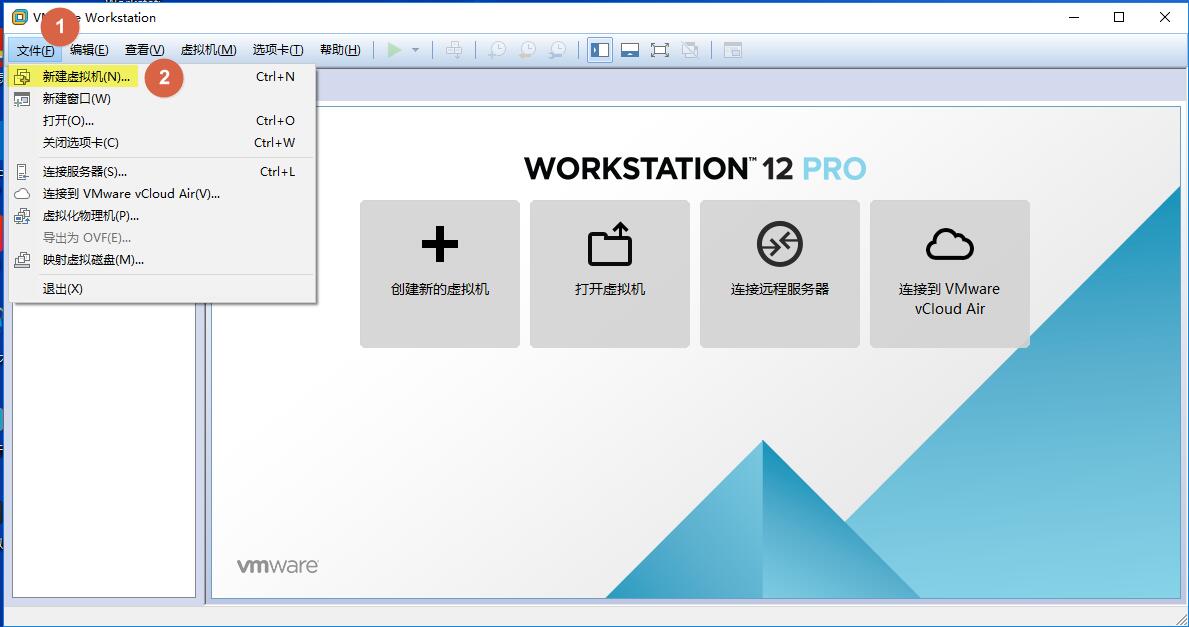
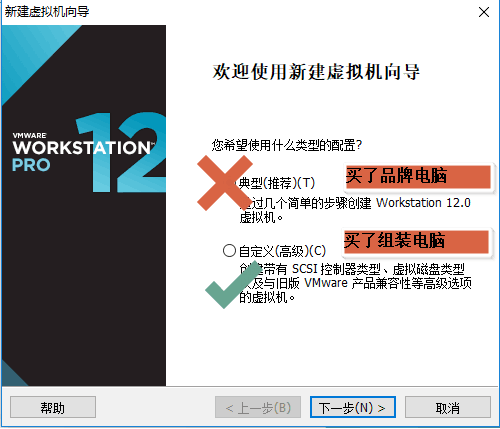
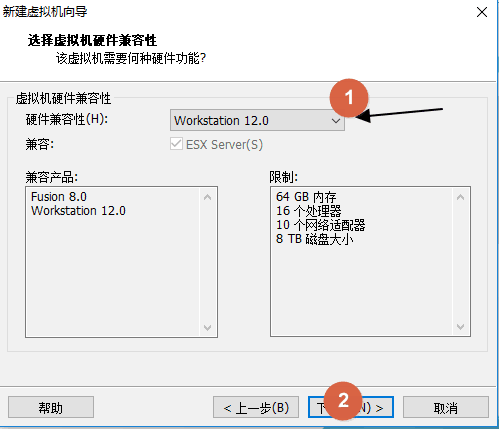
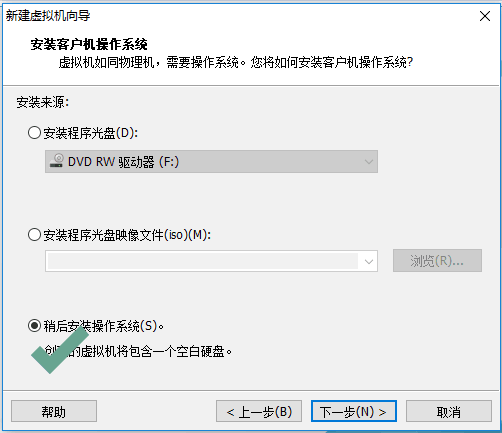
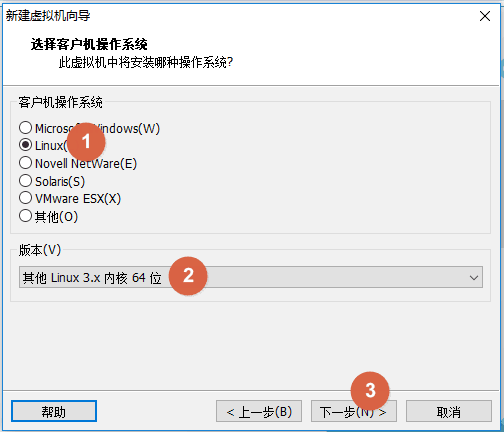
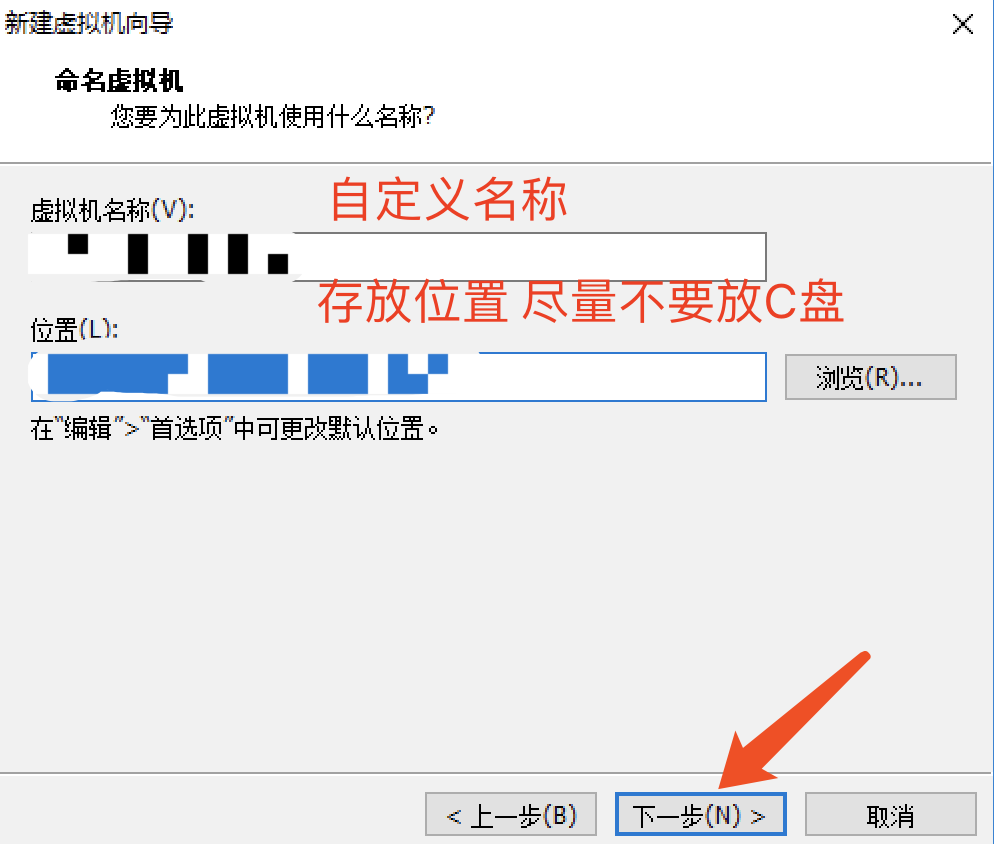
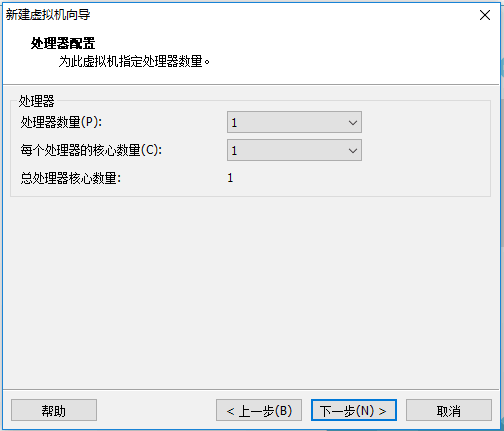
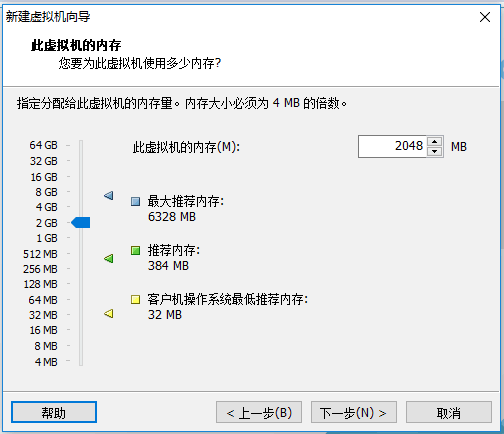
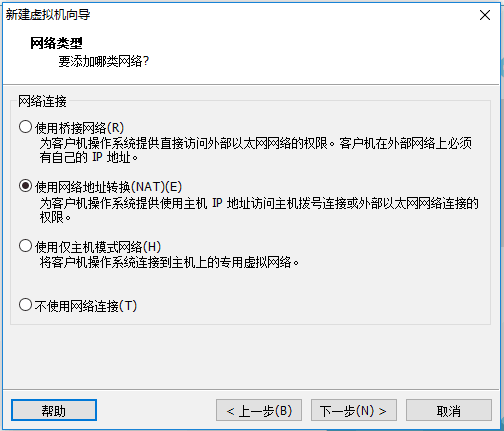
后面几步直接按照推荐的,点击下一步即可
VMware12如何下载
# VMware12下载地址:https://download3.vmware.com/software/wkst/file/VMware-workstation-full-12.5.5-5234757.exe # 激活码:5A02H-AU243-TZJ49-GTC7K-3C61N
注意事项:
内存多分配的话 每个虚拟主机1G(建议)
内存少每个虚拟主机512m 安装系统时建议分配内存2G
配置虚拟主机,参考详细图示即可。
第一步:
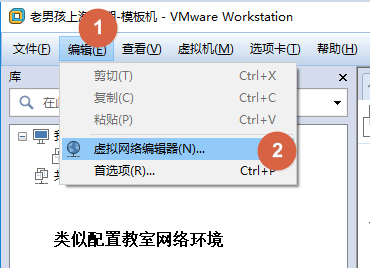
第二步:
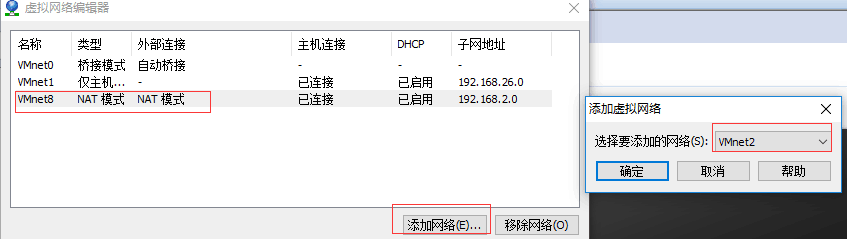
第三步:
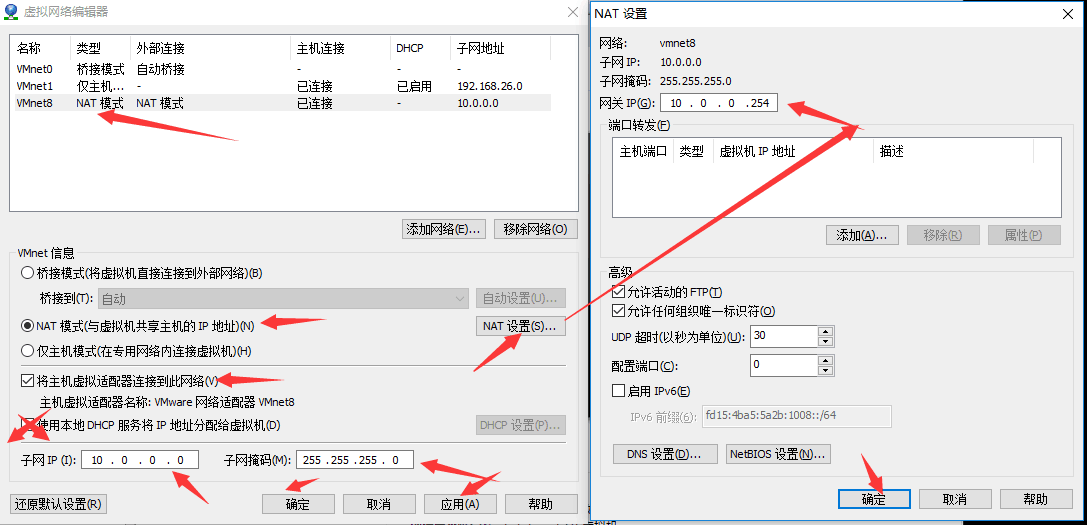
第四步:
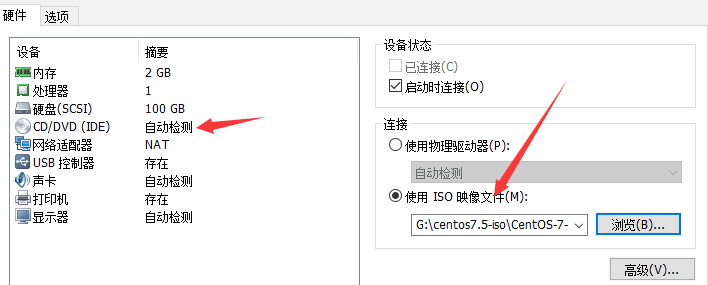
补充知识:
# 有监督学习与无监督学习(课后百度搜索更加全面的解答) 有监督意思就是有明确需要研究的因变量Y 无监督意思就是没有明确需要研究的因变量Y # 算法 算法其实就是研究问题的解决方法 ps:算法工程师就是在研究解决某个问题的最优方法




 浙公网安备 33010602011771号
浙公网安备 33010602011771号