岭回归与lasso等回归模型
模型的假设检验(F与T)
F检验:提出原假设和备择假设 然后计算统计量与理论值 最后进行比较
F检验主要是用来检验模型是否合理的
代码:
# 导入第三方模块 import numpy as np # 计算建模数据中因变量的均值 ybar=train.Profit.mean() # 统计变量个数和观测个数 p=model2.df_model n=train.shape[0] # 计算回归离差平⽅和 RSS=np.sum((model2.fittedvalues-ybar)**2) # 计算误差平⽅和 ESS=np.sum(model2.resid**2) # 计算F统计量的值 F=(RSS/p)/(ESS/(n-p-1)) print('F统计量的值:',F) F统计量的值:174.6372 # 导入模块 from scipy.stats import f # 计算F分布的理论值 F_Theroy = f.ppf(q=0.95, dfn = p,dfd = n-p-1) print('F分布的理论值为:',F_Theroy) out: F分布的理论值为: 2.5026 ''' 计算出来的F统计量值174.64远远⼤于F分布的理论值2.50 所以应当拒绝原假设(先假设模型不合理)
T检验
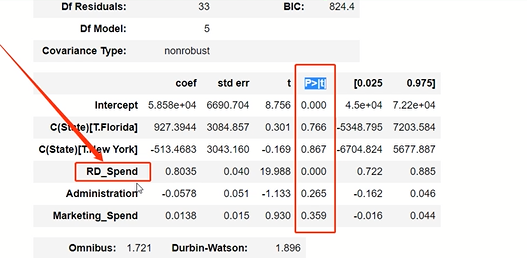
T检验更加侧重于检验模型的各个参数是否合理
model.summary() # 绝对值越小影响越大
线性回归模型的短板
1.自变量的个数大于样本量
2.自变量之间存在多重共线性
所以为了解决这个短板就有了
岭回归模型
理论:
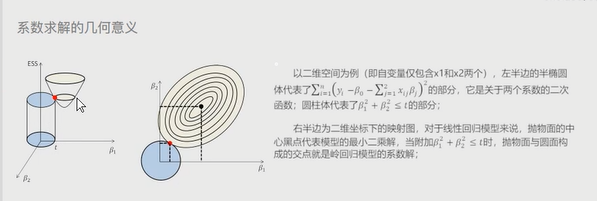
在线性回归模型的基础上添加了一个L2惩罚项(也叫做平方项或者正则项) # 该模型最终转变成求解圆柱体抛物线的焦点问题
图形:
Lasso回归模型
理论:
在线性回归模型的基础上添加了一个L1惩罚项(也叫做绝对值项、正则项) 相较于岭回归,模型的复杂度有所降低 # 该模型最终转变成求解正方体与椭圆抛物线的焦点问题
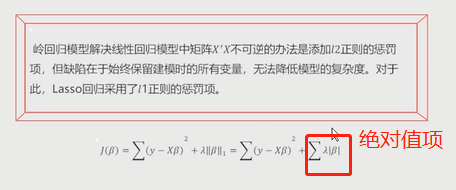
图形:
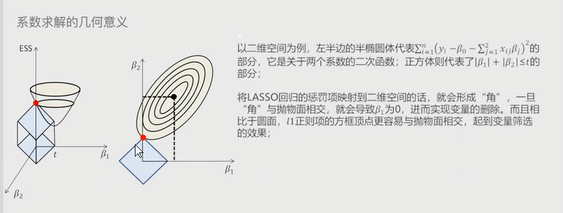
交叉验证
理论:
将所有数据都参与到模型的构建和测试中,最后生成多个模型
再从多个模型中筛选出得分(准确度)最高的模型

岭回归交叉验证:

案例:

# 导入第三方模块 import pandas as pd import numpy as np from sklearn import model_selection from sklearn.linear_model import Ridge,RidgeCV import matplotlib.pyplot as plt # 读取糖尿病数据集 diabetes = pd.read_excel(r'diabetes.xlsx', sep = '') # 构造自变量(剔除患者性别、年龄和因变量) predictors = diabetes.columns[2:-1] # 将数据集拆分为训练集和测试集 X_train, X_test, y_train, y_test = model_selection.train_test_split(diabetes[predictors], diabetes['Y'], test_size = 0.2, random_state = 1234 ) # 构造不同的Lambda值 Lambdas = np.logspace(-5, 2, 200) # 岭回归模型的交叉验证 # 设置交叉验证的参数,对于每一个Lambda值,都执行10重交叉验证 ridge_cv = RidgeCV(alphas = Lambdas, normalize=True, scoring='neg_mean_squared_error', cv = 10) # 模型拟合 ridge_cv.fit(X_train, y_train) # 返回最佳的lambda值 ridge_best_Lambda = ridge_cv.alpha_ ridge_best_Lambda # 导入第三方包中的函数 from sklearn.metrics import mean_squared_error # 基于最佳的Lambda值建模 ridge = Ridge(alpha = ridge_best_Lambda, normalize=True) ridge.fit(X_train, y_train) # 返回岭回归系数 pd.Series(index = ['Intercept'] + X_train.columns.tolist(),data = [ridge.intercept_] + ridge.coef_.tolist()) # 预测 ridge_predict = ridge.predict(X_test) # 预测效果验证 RMSE = np.sqrt(mean_squared_error(y_test,ridge_predict)) RMSE
Lasso回归交叉验证:

案例:

# 导入第三方模块中的函数 from sklearn.linear_model import Lasso,LassoCV # LASSO回归模型的交叉验证 lasso_cv = LassoCV(alphas = Lambdas, normalize=True, cv = 10, max_iter=10000) lasso_cv.fit(X_train, y_train) # 输出最佳的lambda值 lasso_best_alpha = lasso_cv.alpha_ lasso_best_alpha # 基于最佳的lambda值建模 lasso = Lasso(alpha = lasso_best_alpha, normalize=True, max_iter=10000) lasso.fit(X_train, y_train) # 返回LASSO回归的系数 pd.Series(index = ['Intercept'] + X_train.columns.tolist(),data = [lasso.intercept_] + lasso.coef_.tolist()) # 预测 lasso_predict = lasso.predict(X_test) # 预测效果验证 RMSE = np.sqrt(mean_squared_error(y_test,lasso_predict)) RMSE # 导入第三方模块 from statsmodels import api as sms # 为自变量X添加常数列1,用于拟合截距项 X_train2 = sms.add_constant(X_train) X_test2 = sms.add_constant(X_test) # 构建多元线性回归模型 linear = sms.OLS(y_train, X_train2).fit() # 返回线性回归模型的系数 linear.params # 模型的预测 linear_predict = linear.predict(X_test2) # 预测效果验证 RMSE = np.sqrt(mean_squared_error(y_test,linear_predict)) RMSE
Logistic回归模型
将线性回归模型的公式做Logit变换即为Logistic回归模型,将预测问题变成了0到1之间的概率问题

案例:

# 导入第三方模块 import pandas as pd import numpy as np import matplotlib.pyplot as plt # 自定义绘制ks曲线的函数 def plot_ks(y_test, y_score, positive_flag): # 对y_test重新设置索引 y_test.index = np.arange(len(y_test)) # 构建目标数据集 target_data = pd.DataFrame({'y_test':y_test, 'y_score':y_score}) # 按y_score降序排列 target_data.sort_values(by = 'y_score', ascending = False, inplace = True) # 自定义分位点 cuts = np.arange(0.1,1,0.1) # 计算各分位点对应的Score值 index = len(target_data.y_score)*cuts scores = np.array(target_data.y_score)[index.astype('int')] # 根据不同的Score值,计算Sensitivity和Specificity Sensitivity = [] Specificity = [] for score in scores: # 正例覆盖样本数量与实际正例样本量 positive_recall = target_data.loc[(target_data.y_test == positive_flag) & (target_data.y_score>score),:].shape[0] positive = sum(target_data.y_test == positive_flag) # 负例覆盖样本数量与实际负例样本量 negative_recall = target_data.loc[(target_data.y_test != positive_flag) & (target_data.y_score<=score),:].shape[0] negative = sum(target_data.y_test != positive_flag) Sensitivity.append(positive_recall/positive) Specificity.append(negative_recall/negative) # 构建绘图数据 plot_data = pd.DataFrame({'cuts':cuts,'y1':1-np.array(Specificity),'y2':np.array(Sensitivity), 'ks':np.array(Sensitivity)-(1-np.array(Specificity))}) # 寻找Sensitivity和1-Specificity之差的最大值索引 max_ks_index = np.argmax(plot_data.ks) plt.plot([0]+cuts.tolist()+[1], [0]+plot_data.y1.tolist()+[1], label = '1-Specificity') plt.plot([0]+cuts.tolist()+[1], [0]+plot_data.y2.tolist()+[1], label = 'Sensitivity') # 添加参考线 plt.vlines(plot_data.cuts[max_ks_index], ymin = plot_data.y1[max_ks_index], ymax = plot_data.y2[max_ks_index], linestyles = '--') # 添加文本信息 plt.text(x = plot_data.cuts[max_ks_index]+0.01, y = plot_data.y1[max_ks_index]+plot_data.ks[max_ks_index]/2, s = 'KS= %.2f' %plot_data.ks[max_ks_index]) # 显示图例 plt.legend() # 显示图形 plt.show() # 导入虚拟数据 virtual_data = pd.read_excel(r'virtual_data.xlsx') # 应用自定义函数绘制k-s曲线 plot_ks(y_test = virtual_data.Class, y_score = virtual_data.Score,positive_flag = 'P') # 导入第三方模块 import pandas as pd import numpy as np from sklearn import model_selection from sklearn import linear_model # 读取数据 sports = pd.read_csv(r'Run or Walk.csv') # 提取出所有自变量名称 predictors = sports.columns[4:] # 构建自变量矩阵 X = sports.ix[:,predictors] # 提取y变量值 y = sports.activity # 将数据集拆分为训练集和测试集 X_train, X_test, y_train, y_test = model_selection.train_test_split(X, y, test_size = 0.25, random_state = 1234) # 利用训练集建模 sklearn_logistic = linear_model.LogisticRegression() sklearn_logistic.fit(X_train, y_train) # 返回模型的各个参数 print(sklearn_logistic.intercept_, sklearn_logistic.coef_) # 模型预测 sklearn_predict = sklearn_logistic.predict(X_test) # 预测结果统计 pd.Series(sklearn_predict).value_counts() # 导入第三方模块 from sklearn import metrics # 混淆矩阵 cm = metrics.confusion_matrix(y_test, sklearn_predict, labels = [0,1]) cm Accuracy = metrics.scorer.accuracy_score(y_test, sklearn_predict) Sensitivity = metrics.scorer.recall_score(y_test, sklearn_predict) Specificity = metrics.scorer.recall_score(y_test, sklearn_predict, pos_label=0) print('模型准确率为%.2f%%:' %(Accuracy*100)) print('正例覆盖率为%.2f%%' %(Sensitivity*100)) print('负例覆盖率为%.2f%%' %(Specificity*100)) # 混淆矩阵的可视化 # 导入第三方模块 import seaborn as sns import matplotlib.pyplot as plt %matplotlib # 绘制热力图 sns.heatmap(cm, annot = True, fmt = '.2e',cmap = 'GnBu') # 图形显示 plt.show() sklearn_logistic.predict_proba(X_test) # y得分为模型预测正例的概率 y_score = sklearn_logistic.predict_proba(X_test)[:,1] # 计算不同阈值下,fpr和tpr的组合值,其中fpr表示1-Specificity,tpr表示Sensitivity fpr,tpr,threshold = metrics.roc_curve(y_test, y_score) # 计算AUC的值 roc_auc = metrics.auc(fpr,tpr) # 绘制面积图 plt.stackplot(fpr, tpr, color='steelblue', alpha = 0.5, edgecolor = 'black') # 添加边际线 plt.plot(fpr, tpr, color='black', lw = 1) # 添加对角线 plt.plot([0,1],[0,1], color = 'red', linestyle = '--') # 添加文本信息 plt.text(0.5,0.3,'ROC curve (area = %0.2f)' % roc_auc) # 添加x轴与y轴标签 plt.xlabel('1-Specificity') plt.ylabel('Sensitivity') # 显示图形 plt.show() # 调用自定义函数,绘制K-S曲线 plot_ks(y_test = y_test, y_score = y_score, positive_flag = 1) # -----------------------第一步 建模 ----------------------- # # 导入第三方模块 import statsmodels.api as sm # 将数据集拆分为训练集和测试集 X_train, X_test, y_train, y_test = model_selection.train_test_split(X, y, test_size = 0.25, random_state = 1234) # 为训练集和测试集的X矩阵添加常数列1 X_train2 = sm.add_constant(X_train) X_test2 = sm.add_constant(X_test) # 拟合Logistic模型 sm_logistic = sm.Logit(y_train, X_train2).fit() # 返回模型的参数 sm_logistic.params # -----------------------第二步 预测构建混淆矩阵 ----------------------- # # 模型在测试集上的预测 sm_y_probability = sm_logistic.predict(X_test2) # 根据概率值,将观测进行分类,以0.5作为阈值 sm_pred_y = np.where(sm_y_probability >= 0.5, 1, 0) # 混淆矩阵 cm = metrics.confusion_matrix(y_test, sm_pred_y, labels = [0,1]) cm # -----------------------第三步 绘制ROC曲线 ----------------------- # # 计算真正率和假正率 fpr,tpr,threshold = metrics.roc_curve(y_test, sm_y_probability) # 计算auc的值 roc_auc = metrics.auc(fpr,tpr) # 绘制面积图 plt.stackplot(fpr, tpr, color='steelblue', alpha = 0.5, edgecolor = 'black') # 添加边际线 plt.plot(fpr, tpr, color='black', lw = 1) # 添加对角线 plt.plot([0,1],[0,1], color = 'red', linestyle = '--') # 添加文本信息 plt.text(0.5,0.3,'ROC curve (area = %0.2f)' % roc_auc) # 添加x轴与y轴标签 plt.xlabel('1-Specificity') plt.ylabel('Sensitivity') # 显示图形 plt.show() # -----------------------第四步 绘制K-S曲线 ----------------------- # # 调用自定义函数,绘制K-S曲线 sm_y_probability.index = np.arange(len(sm_y_probability)) plot_ks(y_test = y_test, y_score = sm_y_probability, positive_flag = 1)
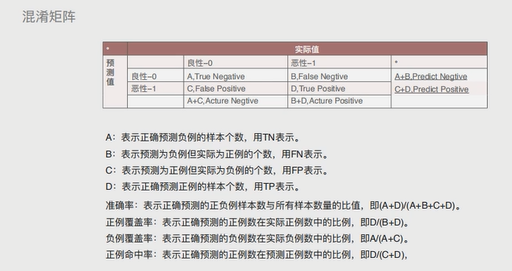
混淆矩阵
准确率:表示正确预测的正负例样本数与所有样本数量的比值,即(A+B)/(A+B+C+D) 正例覆盖率:表示正确预测的正例数在实际正例数中的比利,即D/(B+D) 负例覆盖率:表示正确预测的负例数在实际负例数中的比利,即A/(A+C) 正例命中率:表示正确预测的正例数在预测正例数中的比利,即D/(C+D)
决策树与随机森林
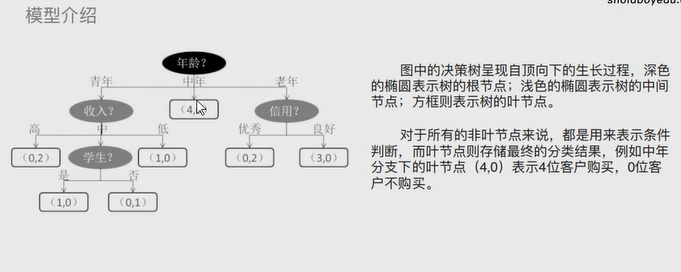
作用:
默认情况下解决分类问题(买与不买、带与不带、走与不走)
也可以切换算法解决预测问题(具体数值多少)。
树:
其实就是一种计算机底层的数据结构,与现实中的树不同,计算机中的树是自上而下生长的。
决策树:
是算法模型中的一种概念,有三个主要部分:根节点、枝节点、叶子节点。
根节点与枝节点用于存放条件,叶子节点存放真正的数据结果
1.信息熵

eg:信息熵小相当于红绿灯情况,信息熵大相当于买彩票中奖情况。
2.条件熵
条件熵其实就是由信息熵再次细分而来的。
eg:比如有九个用户购买了商品五个没有购买,那么条件熵就是继续从购不购买的用户中在选择一个条件。
3.信息增益

信息增益可以反映出某个条件是否对最终的分类有决定性的影响。
在构建决策树时根节点与枝节点所放的条件按照信息增益由大到小排列。
4.信息增益率

决策树中的ID3碎发使用信息增益指标实现根节点或中间节点的字段选择,但是该指标存在一个非常明显的缺点,即信息增益会偏向于取值较多的字段。
所以为了克服信息增益指标的缺点,提出了信息增益率的概念,他的思想很简单,就是在信息增益的基础上进行相应的惩罚。
基尼指数与基尼指数增益
基尼指数:可以让模型解决预测问题。
基尼指数增益:与信息增益相似,还需要考虑自变量对因变量的影响程度,即因变量的基尼指数下降速度的快慢,下降的越快,自变量对应变量的影响就越强。
随机森林

""" 随机森林中每颗决策树都不限制节点字段选择,有多棵树组成的随机森林 在解决分类问题的时候采用投票法、解决预测问题的时候采用均值法 """
泰坦尼克案例:

# 导入第三方模块 import pandas as pd import numpy as np import matplotlib.pyplot as plt from sklearn import model_selection from sklearn import linear_model # 读⼊数据 Titanic = pd.read_csv(r'Titanic.csv') Titanic # 删除⽆意义的变量,并检查剩余变量是否含有缺失值 Titanic.drop(['PassengerId','Name','Ticket','Cabin'], axis = 1, inplace = True) Titanic.isnull().sum(axis = 0) # 对Sex分组,⽤各组乘客的平均年龄填充各组中的缺失年龄 fillna_Titanic = [] for i in Titanic.Sex.unique(): update = Titanic.loc[Titanic.Sex == i,].fillna(value = {'Age': Titanic.Age[Titanic.Sex == i].mean()}, inplace = False) fillna_Titanic.append(update) Titanic = pd.concat(fillna_Titanic) # 使⽤Embarked变量的众数填充缺失值 Titanic.fillna(value = {'Embarked':Titanic.Embarked.mode()[0]}, inplace=True) # 将数值型的Pclass转换为类别型,否则⽆法对其哑变量处理 Titanic.Pclass = Titanic.Pclass.astype('category') # 哑变量处理 dummy = pd.get_dummies(Titanic[['Sex','Embarked','Pclass']]) # ⽔平合并Titanic数据集和哑变量的数据集 Titanic = pd.concat([Titanic,dummy], axis = 1) # 删除原始的Sex、Embarked和Pclass变量 Titanic.drop(['Sex','Embarked','Pclass'], inplace=True, axis = 1) # 取出所有⾃变量名称 predictors = Titanic.columns[1:] # 将数据集拆分为训练集和测试集,且测试集的⽐例为25% X_train, X_test, y_train, y_test = model_selection.train_test_split(Titanic[predictors], Titanic.Survived, test_size = 0.25, random_state = 1234) from sklearn.model_selection import GridSearchCV # 预设各参数的不同选项值 max_depth = [2,3,4,5,6] min_samples_split = [2,4,6,8] min_samples_leaf = [2,4,8,10,12] # 将各参数值以字典形式组织起来 parameters = {'max_depth':max_depth, 'min_samples_split':min_samples_split, 'min_samples_leaf':min_samples_leaf} # ⽹格搜索法,测试不同的参数值 grid_dtcateg = GridSearchCV(estimator = tree.DecisionTreeClassifier(), param_grid = parameters, cv=10) # 模型拟合 grid_dtcateg.fit(X_train, y_train) # 返回最佳组合的参数值 grid_dtcateg.best_params # 构建分类决策树 CART_Class = tree.DecisionTreeClassifier(max_depth=3,min_samples_leaf=4,min_samples_split=2) # 模型拟合 decision_tree = CART_Class.fit(X_train,y_train) # 模型在测试集上的预测 pred = CART_Class.predict(X_test) # 模型的准确率 print(‘模型在测试集的预测准确率:\n',metrics.accuracy_score(y_test,pred)) print('模型在训练集的预测准确率:\n', metrics.accuracy_score(y_train,ꢀCART_Class.predict(X_train)))
K近邻模型
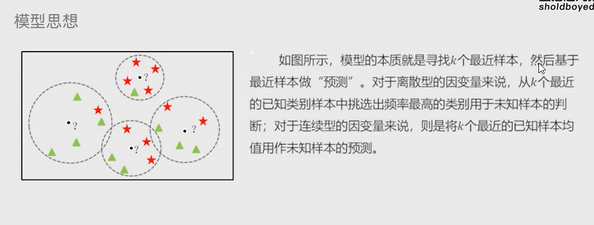
思想:根据未知样本点周围的K个邻居样本完成预测或者分类。
K近邻模型既可以解决分类问题也可以解决预测问题
K值的选择:
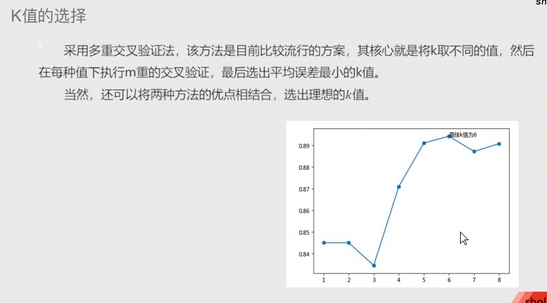
1.先猜测 2.交叉验证 3.作图选择最合理的k值 准确率,越大越好 MSE,越小越好
过拟合与欠拟合

距离:
欧式距离:两点之间的直线距离
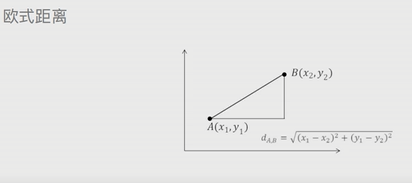
曼哈顿距离:默认两点之间有障碍物
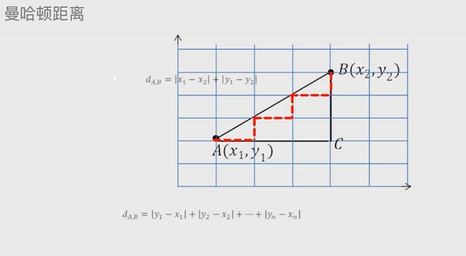
余弦相似度:应用于论文查重
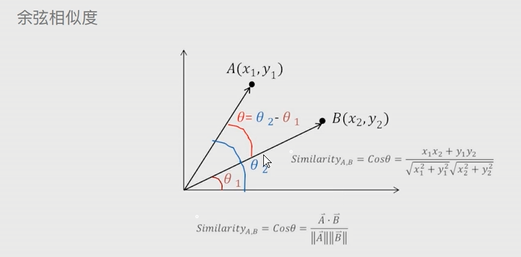
案例一:

# 导入第三方包 import pandas as pd # 导入数据 Knowledge = pd.read_excel(r'Knowledge.xlsx') # 返回前5行数据 Knowledge.head() # 构造训练集和测试集 # 导入第三方模块 from sklearn import model_selection # 将数据集拆分为训练集和测试集 predictors = Knowledge.columns[:-1] predictors X_train, X_test, y_train, y_test = model_selection.train_test_split(Knowledge[predictors], Knowledge.UNS, test_size = 0.25, random_state = 1234) # 导入第三方模块 import numpy as np from sklearn import neighbors import matplotlib.pyplot as plt # 设置待测试的不同k值 K = np.arange(1,np.ceil(np.log2(Knowledge.shape[0]))).astype(int) # 构建空的列表,用于存储平均准确率 accuracy = [] for k in K: # 使用10重交叉验证的方法,比对每一个k值下KNN模型的预测准确率 cv_result = model_selection.cross_val_score(neighbors.KNeighborsClassifier(n_neighbors = k, weights = 'distance'), X_train, y_train, cv = 10, scoring='accuracy') accuracy.append(cv_result.mean()) # 从k个平均准确率中挑选出最大值所对应的下标 arg_max = np.array(accuracy).argmax() # 中文和负号的正常显示 plt.rcParams['font.sans-serif'] = ['Microsoft YaHei'] plt.rcParams['axes.unicode_minus'] = False # 绘制不同K值与平均预测准确率之间的折线图 plt.plot(K, accuracy) # 添加点图 plt.scatter(K, accuracy) # 添加文字说明 plt.text(K[arg_max], accuracy[arg_max], '最佳k值为%s' %int(K[arg_max])) # 显示图形 plt.show() # 导入第三方模块 from sklearn import metrics # 重新构建模型,并将最佳的近邻个数设置为6 knn_class = neighbors.KNeighborsClassifier(n_neighbors = 6, weights = 'distance') # 模型拟合 knn_class.fit(X_train, y_train) # 模型在测试数据集上的预测 predict = knn_class.predict(X_test) # 构建混淆矩阵 cm = pd.crosstab(predict,y_test) cm # 导入第三方模块 import seaborn as sns # 将混淆矩阵构造成数据框,并加上字段名和行名称,用于行或列的含义说明 cm = pd.DataFrame(cm) # 绘制热力图 sns.heatmap(cm, annot = True,cmap = 'GnBu') # 添加x轴和y轴的标签 plt.xlabel(' Real Lable') plt.ylabel(' Predict Lable') # 图形显示 plt.show() # 模型整体的预测准确率 metrics.scorer.accuracy_score(y_test, predict)
案例二:

# 读入数据 ccpp = pd.read_excel(r'CCPP.xlsx') ccpp.head() # 返回数据集的行数与列数 ccpp.shape ######################################### # 导入第三方包 from sklearn.preprocessing import minmax_scale # 对所有自变量数据作标准化处理(统一量纲) predictors = ccpp.columns[:-1] X = minmax_scale(ccpp[predictors]) ######################################### # 将数据集拆分为训练集和测试集 X_train, X_test, y_train, y_test = model_selection.train_test_split(X, ccpp.PE, test_size = 0.25, random_state = 1234) # 设置待测试的不同k值 K = np.arange(1,np.ceil(np.log2(ccpp.shape[0]))).astype(int) # 构建空的列表,用于存储平均MSE mse = [] for k in K: # 使用10重交叉验证的方法,比对每一个k值下KNN模型的计算MSE cv_result = model_selection.cross_val_score(neighbors.KNeighborsRegressor(n_neighbors = k, weights = 'distance'), X_train, y_train, cv = 10, scoring='neg_mean_squared_error') mse.append((-1*cv_result).mean()) # 从k个平均MSE中挑选出最小值所对应的下标 arg_min = np.array(mse).argmin() # 绘制不同K值与平均MSE之间的折线图 plt.plot(K, mse) # 添加点图 plt.scatter(K, mse) # 添加文字说明 plt.text(K[arg_min], mse[arg_min] + 0.5, '最佳k值为%s' %int(K[arg_min])) # 显示图形 plt.show() # 重新构建模型,并将最佳的近邻个数设置为7 knn_reg = neighbors.KNeighborsRegressor(n_neighbors = 7, weights = 'distance') # 模型拟合 knn_reg.fit(X_train, y_train) # 模型在测试集上的预测 predict = knn_reg.predict(X_test) # 计算MSE值 metrics.mean_squared_error(y_test, predict) # 对比真实值和实际值 pd.DataFrame({'Real':y_test,'Predict':predict}, columns=['Real','Predict']).head(10) # 导入第三方模块 from sklearn import tree # 预设各参数的不同选项值 max_depth = [19,21,23,25,27] min_samples_split = [2,4,6,8] min_samples_leaf = [2,4,8,10,12] parameters = {'max_depth':max_depth, 'min_samples_split':min_samples_split, 'min_samples_leaf':min_samples_leaf} # 网格搜索法,测试不同的参数值 grid_dtreg = model_selection.GridSearchCV(estimator = tree.DecisionTreeRegressor(), param_grid = parameters, cv=10) # 模型拟合 grid_dtreg.fit(X_train, y_train) # 返回最佳组合的参数值 grid_dtreg.best_params_ # 构建用于回归的决策树 CART_Reg = tree.DecisionTreeRegressor(max_depth = 25, min_samples_leaf = 10, min_samples_split = 4) # 回归树拟合 CART_Reg.fit(X_train, y_train) # 模型在测试集上的预测 pred = CART_Reg.predict(X_test) # 计算衡量模型好坏的MSE值 metrics.mean_squared_error(y_test, pred)







 浙公网安备 33010602011771号
浙公网安备 33010602011771号