题解：AT_abc346_e [ABC346E] Paint

思路

定义矩阵为 $a$。

显然不能在线处理，否则 $10^{10}$ 的复杂度一定 $\tt TLE$。

考虑每一次操作所可以覆盖的格子，离线处理。

不同的列和列是互不干扰的，行同理。

行和列是干扰的，因为覆盖的是整行整列，所以它们一定互相干扰对方。如果第 $i$ 行（颜色为 $p$）在第 $j$ 列（颜色为 $q$）之后覆盖，那么 $a_{i,j}$ 的颜色会变为 $p$ 而不是 $q$。

如果有一行被覆盖了多次，我们只需要看最后一次。

我们造一组样例：

3 4 5
1 3 2
2 3 1
2 4 3
1 3 4
2 2 3

变化顺序将如下图所示：

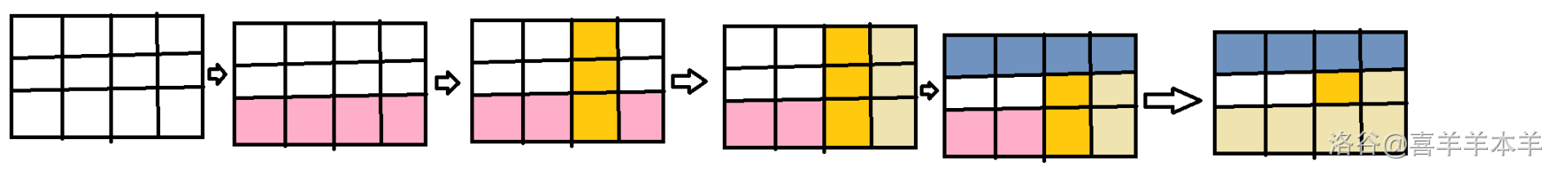
如果我们倒序考虑最终结果图，那么会发现：

• 第 $5$ 次操作因为是最后一次，所以每一个格子都能覆盖上。
• 第 $4$ 次操作虽然不是最后一次，但是后面并没有列来干扰它了，所以也是每一个格子都能覆盖上。
• 第 $3$ 次操作操作的是列，但是它后面已经有两行被提前覆盖了，所以它只能覆盖 $1$ 格。
• 第 $2$ 次同理。
• 第 $1$ 次操作覆盖的第 $3$ 行第 $5$ 次操作已经覆盖过了，一个都不能覆盖。

这就是最终的结果图。

那么，最后会留下一些为 $0$ 的颜色格子，这些该怎么考虑呢？

有两种方法。

1. 数学法：$0$ 的数量就是全部的数量 $-$ 被覆盖的数量。具体来说，如果 $m$ 行 $n$ 列被覆盖，则剩余 $0$ 数量应为 $h\times w-m\times w-n\times h+n\times m$。
2. 暴力法。我们可以看成开局的全是 $0$ 是进行了 $h+w$ 次操作，每一次都覆盖成 $0$ 造成的，这样增加了 $\operatorname{O}(h+w)$ 的时间复杂度，但是仍然可以通过。

代码实现

显然我们可以记录数组表示操作，不过我这里用了一个栈。

栈满足后进先出的原则，调试更加方便。

还有答案数组要开 $\texttt{long long}$！不要忘记输出总和！

Code（暴力法）：

#include<bits/stdc++.h>
using namespace std;
int h,l,m,opt,x,y;
long long ans[200005];
bool f[200005][3];
stack<int>st1;
stack<int>st2;
stack<int>st3;
int main(){
	cin>>h>>l>>m;
	for(int i=1;i<=h;i++){
		st1.push(1);
		st2.push(i);
		st3.push(0);
	}
	for(int i=1;i<=l;i++){
		st1.push(2);
		st2.push(i);
		st3.push(0);
	}
	while(m--){
		cin>>opt>>x>>y;
		st1.push(opt);
		st2.push(x);
		st3.push(y); 
	}
	int hang=0,lie=0;
	while(!st1.empty()){
		opt=st1.top();
		x=st2.top();
		y=st3.top();
		st1.pop();st2.pop();st3.pop();
		if(f[x][opt]==1)continue;
		f[x][opt]=1;
		if(opt==1){
			ans[y]+=(l-lie);
			hang++;
		}
		else{
			ans[y]+=(h-hang);
			lie++;
		}
	}
	int sum=0;
	for(int i=0;i<=200000;i++){
		if(ans[i]>0)sum++;
	}
	cout<<sum<<endl;
	for(int i=0;i<=200000;i++){
		if(ans[i]>0)cout<<i<<' '<<ans[i]<<endl;
	}
	return 0;
}