题解：UVA1362 Exploring Pyramids

双倍经验：P10956。

Solution UVA1362

Problem

给定一棵树的 dfs 遍历顺序，求其可能对应的树的个数。

Idea

不难发现每一次我们到达一个点，都会立即开始遍历它的子树，经过若干次遍历再回到这个点，然后进行遍历它的下一个子树（如果没有子树了就返回父亲）。

因此，一个树的 dfs 遍历序列一定形如 $\{x,y,\cdots,y,\cdots,y,x,\cdots,x\}$。

还不理解？看图：

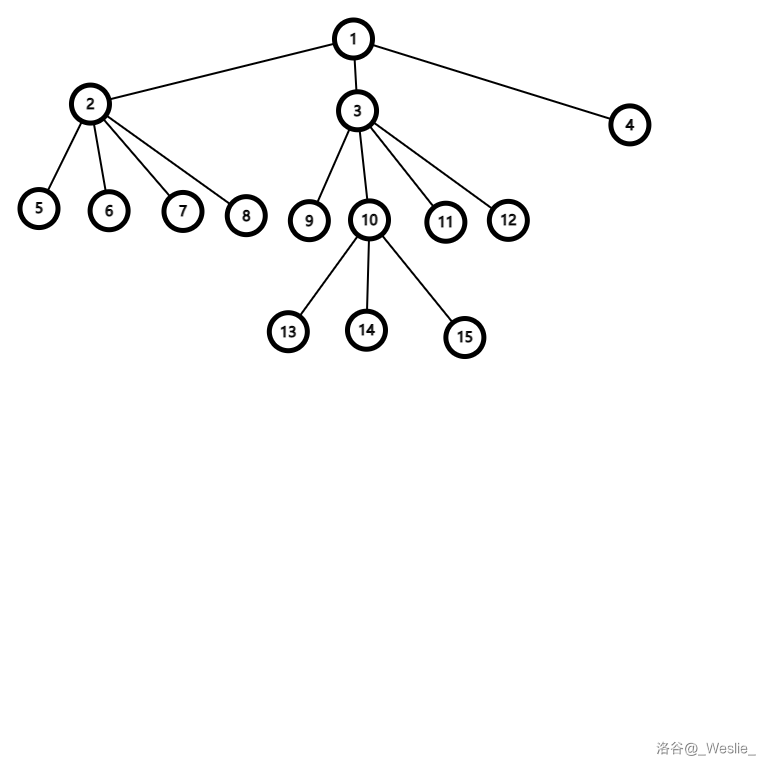
我们从点 $1$ 出发，设遍历序列为 $a$。

先遍历到 $2$，$a=\{1,2\}$。

然后遍历到 $5$，$a=\{1,2,5\}$。

然后回到 $2$，$a=\{1,2,5,2\}$。

然后依次遍历 $6$、$7$、$8$，最后回到 $1$，则 $a=\{1,2,5,2,6,2,7,2,8,2,1\}$。

然后遍历子树 $3$ 和 $4$，则 $a=\{1,2,5,2,6,2,7,2,8,2,1,3,9,3,10,13,10,14,10,15,10,3,11,3,12,3,1,4,1\}$。

因此，我们发现一个数 $x$ 一定会在遍历序列中输出 $son_x+1$ 次（其中 $son_x$ 为 $x$ 的儿子的个数）。

我们发现每个子树都是相互独立的，即一个子树的统计结果不会影响没有包含关系的另一个子树的统计结果。

这个信息显然是可合并的，所以可以区间 $dp$。

设 $dp_{i,j}$ 为 $[i,j]$ 区间的方案数。

则显然有：$dp_{i,j}=\sum_{}^{}(dp_{i,k}\times dp_{k+1,j-1})$，其中 $i\le k<j$ 且 $s_i=s_k=s_j$。

解释一下就是枚举断点，使得 $[i+1,k-1]$ 和 $[k+1,j-1]$ 变为两个不同子树。

答案就是 $dp_{1,n}$。

Code

#include<bits/stdc++.h>
using namespace std;
const int N=305,mod=1000000000;
string s;
int n;
long long dp[N][N];
int main(){
	while(cin>>s){
		n=s.length();
		s=' '+s;
		memset(dp,0,sizeof(dp));
		for(int i=1;i<=n;i++)dp[i][i]=1ll;
		for(int len=2;len<=n;len++){
			for(int i=1,j=len;j<=n;j++,i++){
				if(s[i]!=s[j])continue;
				for(int k=i;k<j;k++){
					if(s[k]!=s[i])continue;
					dp[i][j]=dp[i][j]+dp[i][k]*dp[k+1][j-1]%mod;
					dp[i][j]%=mod;
				}
			}
		} 
		printf("%lld\n",dp[1][n]);	
	}	
	return 0;
}