博弈论

\(\textup{斐波那契博弈}\)

一堆 \(n\) 个石子，每次取不超过前一次的两倍的石子，取走最后一个石子为胜。先手不能第一次取完石子。

先给结论：

当且仅当 \(n\) 为 \(\mathtt{Fibonacci}\) 数时，先手必败。

• \(\mathtt{Zeckendorf}\) 定理：一个正整数可以分解为若干个不连续的 \(\mathtt{Fibonacci}\) 数 之和。

证明如下：

\(1.\) 当 \(n\) 为 \(\mathtt{Fibonacci}\) 数时，先手必败。

数学归纳法：

设 \(n\) 是第 \(k + 1\) 个 \(\mathtt{Fibonacci}\) 数，即 \(n = f_{k + 1}= f_{k - 1} + f_{k}\)

将 \(n\) 个石子分为两堆： \(f_{k}\) 堆和 \(f_{k - 1}\) 堆。先手一定不能取大于等于 \(f_{k - 1}\) 堆的石子，因为 \(f_{k - 1} * 2 \ge f_{k}\)。

那么就考虑先手先操作 \(f_{k - 1}\) 堆，由于这是两个子问题，假设取 \(f_{k - 1}\) 先手必败成立，那么我们关心的就是后手取完 \(f_{k - 1}\) 堆时先手取不完 \(f_k\) 堆。

先手的最优策略一定是取 \(\frac{1}{3}f_{k - 1}\) 个石子，取大于 \(\frac{1}{3}f_{k - 1}\) 堆不仅可以让后手取完 \(f_{k - 1}\) 堆，而且会让后手取得更少，从而先手更难取完 \(f_k\) 堆。

那么我们就要证明 \(\frac{2}{3}f_{k - 1} < \frac{1}{2}f_k\)

\[\frac{2}{3}f_{k - 1} < \frac{1}{2}f_k \Longleftrightarrow 4f_{k - 1} < 3f_k\Longleftrightarrow \]

\[\Longrightarrow 3(f_{k - 1} + f_{k - 2}) - 4f_{k - 1} > 0 \Longleftrightarrow 3f_{k - 2} - f_{k - 1} > 0 \]

显然成立。

边界条件为 \(n = 2\) 成立。

\(2.\) 当 \(n\) 不为 \(\mathtt{Fibonacci}\) 数时，先手必胜。

根据 \(\mathtt{Zeckendorf}\) 定理，将 \(n\) 分解为 \(f_{a_1} + f_{a_2} + ... + f_{a_p}\)，且 \(a_1 > a_2 > ... > a_p\)。

因为 \(a_p + 1 < a_{p - 1}\)，有 \(2*f_{a_p} < f_{a_{p - 1}}\)，也就是说先手取完 \(f_p\) 堆后，后手取不玩 \(f_{p - 1}\) 堆，由 \(1\) 可知形成了 \(\mathtt{P}\) 态，此时先手一定能取到 \(f_{p - 1}\) 堆的最后一颗石子，也能取到接下来每一堆的最后一颗，先手必胜。

\(\textup{Nim 博弈}\)

有 \(n\) 堆石子，每堆有 \(a_i\) 个。两人取石子，每人每次选一堆当前石子数为 \(a_i\) 的堆 \(i\)， 任取 \(x\) \((1 \le x \le a_i)\) 个石子，取走最后一堆石子的人获胜。

先给出结论：当 \(a_1 \oplus a_2 \oplus ... \oplus a_n = 0\) 时，先手必败，否则必胜。

尝试证明它， 有以下三个结论：

• 当 \(a_1 + a_2 + ... + a_n = 0\) 时，没有后继状态，\(a_1 \oplus a_2 \oplus ... \oplus a_n = 0\)，必败。

• 当 \(a_1 \oplus a_2 \oplus ... \oplus a_n \ne 0\) 时，一定存在一种取石子的方法，使取完后 \(a_1 \oplus a_2 \oplus ... \oplus a_n = 0\)。

• 当 \(a_1 \oplus a_2 \oplus ... \oplus a_n = 0\) 时，一定不存在一种取石子的方法，使取完后 \(a_1 \oplus a_2 \oplus ... \oplus a_n = 0\)。

对于第二条，设 \(a_1 \oplus a_2 \oplus ... \oplus a_n = k\)。

假设要把 \(a_i\) 变为 \(a_i'\)，则 \(a_i' = a_i \oplus k\)，\(k\) 的最高位 \(1\) 为 \(j\)，显然能找到一个 \(a_i\) 满足 \(a_i\) 的第 \(j\) 位为 \(1\)，此时 \(a_i > a_i \oplus k\)，将 \(a_i\) 赋为 \(a_i \oplus k\) 即可满足异或和为 \(0\)。

\(\textup{博弈图}\)

假设我们正在进行一场酣畅淋漓的 \(\mathtt{Nim}\) 博弈，现在还剩下 \(a_1 = 1, a_2 = 1, a_3 = 2\) 的石子。可以根据接下来的操作和得到的状态画出一张如下的图。

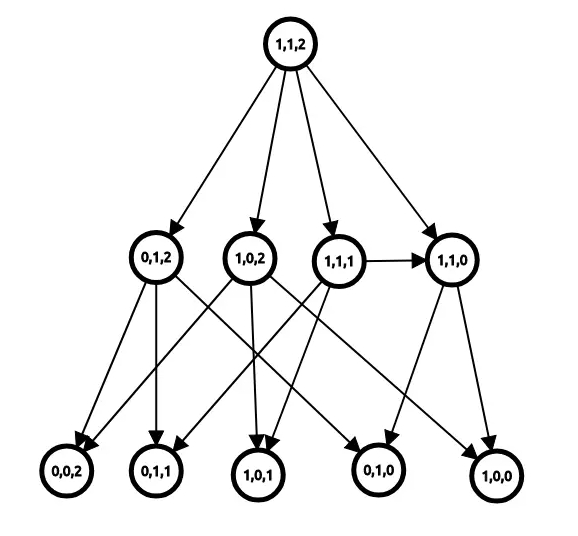
感谢 oiwiki 的馈赠

这张图很有意思，你会发现没有出边的点代表的状态都是必胜态 \((\mathtt{N})\) ——取一次就取完了。出边对应的全是必胜态的点是必败态 \((\mathtt{P})\)，而出边对应的存在必败态的点又是必胜态。

很好理解——怎么走对手都必胜，那不就是必败，能让对手必败，不就是必胜吗？

对于一些状态数和转移数都控制在合理范围内，可以用 \(\mathcal{O}(N + M)\) (状态数，转移数) 的时间通过处理 \(\mathtt{DAG}\) 来求解必胜必败态。

\(\textup{SG 函数和 SG 定理}\)

有这样一个游戏：给定一个 \(\mathtt{DAG}\) 和起点，有一个棋子在起点上，轮流通过有向图上的边移动棋子，不能移动判负。

欸，这不和上文讲的博弈图的东西很像吗？我们可以通过对必胜态和必败态的处理解决。

问题来了：有 \(n\) 个这样的组合游戏，轮流任意移动一个游戏中的棋子，所有游戏都不能移动判负。

\(\textup{mex函数}\)

给定一个数的集合 \(A = {a_1, a_2 ... a_n}\)，定义 \(\mathrm{mex}\{ A \}\) 为 \(A\) 中未出现的最小的数。

举例：\(A = \{0, 1, 4, 3, 5 \}\)，则 \(\mathrm{mex}\{ A \} = 2\)。

\(\textup{SG函数}\)

设当前状态为 \(x\)，后继状态为 \(y_1, y_2...y_m\)，则 \(SG(x) = \mathrm{mex}\{SG(y_1),SG(y_2)...SG(y_m) \}\)。

举个例子，依然是取石子游戏，只不过只有 \(1\) 堆 \(num\) 个石子，且每次只能取 \(1, 2, 4\) 个。

• \(num = 0\)，没有后继态，\(SG(0) = 0\)

• \(num = 1\)，后继态为 \(num = 0\)，\(SG(1) = 1\)

• \(num = 2\)，后继态为 \(num = 0\) 和 \(num = 1\)，\(SG(2) = \mathrm{mex}\{SG(0),SG(1)\} = 2\)。

• \(num = 3\)，后继态为 \(num = 1\) 和 \(num = 2\)，\(SG(3) = \mathrm{mex}\{SG(1),SG(2)\} = 0\)。

• \(num = 4\)，后继态为 \(num = 0\)， \(num = 2\) 和 \(num = 3\)，\(SG(3) = \mathrm{mex}\{SG(1),SG(2)\} = 1\)。

• \(...\)

你或许发现了，\(\mathtt{SG}\) 函数值为 0 时，为必败态，否则为必胜态，这也很好理解，\(SG(x) \ne 0\) 说明 \(x\) 的后继态有满足 \(SG(y) = 0\) 为必败态，则 \(x\) 为必胜态。

\(\textup{SG 定理}\)

接下来我们可以解决上面遗留的问题了：对于 \(n\) 个这样的组合游戏，该怎么求解？

先给结论：

设起点分别为 \(a_1, a_2 ... a_n\) 时，当 \(SG(a_1) \oplus SG(a_2) \oplus ... \oplus SG(a_n) = 0\) 时，先手必败，否则必胜。即一个游戏的 \(\mathtt{SG}\) 函数值等于各个游戏的 \(\mathtt{SG}\) 函数值的 \(\mathtt{Nim}\) 和。

感性理解：

如果一个状态 \(x\) 满足 \(SG(x) = w\)，则这个状态一定可以到达 \(0, 1, ... w - 1\) 的状态，那么这是不是相当于 \(\mathtt{Nim}\) 游戏中的取石子呢？

但是也有向 \(\mathtt{SG}\) 函数值较大的状态移动的操作，我们可以证明这是无效的，就好似 \(\mathtt{Nim}\) 游戏中加石子，到最后还是可以一下取走，向 \(\mathtt{SG}\) 函数值较大的状态移动，还是可以移动会所有函数值较小的状态。

\(\textup{反常游戏}\)

最常见的就是反常 \(\mathtt{Nim}\) 游戏，取走最后一堆石子的人败。

先给结论：

• 当 \(a_1 = a_2 = ... = a_n = 1\) 时，\(n\) 为奇数是 \(\mathtt{P}\) 态， \(n\) 为偶数是 \(\mathtt{N}\)。

• 当有 \(a_i > 1\) 时， \(a_1 \oplus a_2 \oplus ... \oplus a_n = 0\) 时为 \(\mathtt{P}\) 态，否则为 \(\mathtt{N}\) 态。

尝试证明：

第一条显然，因为每次会取完一堆。

对于第二条，分讨一下：

\(1.\) 只有一个 \(a_i > 1\) ：可以确定 \(a_1 \oplus a_2 \oplus ... \oplus a_n \ne 0\) ，此时为 \(\mathtt{N}\) 态，因为先手可以决定将这对取完或者留下一个，也就是说先手可以将游戏转化为第一条的情况，而且可以控制剩余石子奇偶性。

\(2.\) 有两个或以上 \(a_i > 1\) ：

• \(2.1.\ a_1 \oplus a_2 \oplus ... \oplus a_n \ne 0\)：由上文提及的 \(\mathtt{Nim}\) 和的证明可知：一定存在一种方法可以使 \(a_1' \oplus a_2' \oplus ... \oplus a_n' = 0\)，且不会取完任何一堆石子，依然剩下不小于两堆石子 \(a_i > 1\)。

• \(2.2.\ a_1 \oplus a_2 \oplus ... \oplus a_n = 0\)：任意操作肯定会使\(a_1' \oplus a_2' \oplus ... \oplus a_n' \ne 0\)，此时就又转化为 \(2.1\) 的情况，而且随着取石子的过程进行，最后一定是这种情况取完后会出现情况 \(1\)，也就是说 \(2.2\) 的状态为 \(\mathtt{P}\)态，\(2.1\) 的状态为 \(\mathtt{N}\) 态。

得证。

\(\textup{Anti-SG}\)

也就是反常游戏，决策集合为空的游戏者胜。

规定当游戏结束时 \(\mathtt{SG}\) 函数值为 \(0\)，则先手必胜当且仅当：

• \(\mathtt{SG}\) 函数不为 \(0\) 且游戏中某个单一游戏的 \(\mathtt{SG}\) 函数值大于 \(1\)。

• \(\mathtt{SG}\) 函数为 \(0\) 且没有某个单一游戏的 \(\mathtt{SG}\) 函数大于 \(1\)。

\(\textup{Multi-SG}\)

相比平常的博弈，\(\mathtt{Multi-SG}\) 增加了一个操作，将一个游戏拆成两个游戏。

结论：将状态为 \(x\) 拆分，相当于增加 \(SG(x - i) \oplus SG(i)\) 的一个状态。

因为后手可以选择两个状态中的任意一个操作，所以后继的状态的应该是这两个状态的和。那么只需求出两个后继的 \(\mathtt{SG}\) 值然后异或计入后继。

\(\textup{Every-SG}\)

有很多单一游戏，每次每个玩家需要在每一个能够操作的单一游戏上进行操作，最后结束的那个单一游戏的胜负决定整个游戏的胜负。

很明显，对于先手而言，必胜的单一游戏要延长操作次数，必败的单一游戏要减小操作次数。

所以对于每个状态 \(x\)，记录一个理想操作步数 \(stp_x\)，代表作为先手结束游戏的步数。

• \(x = 0\)，结束态，\(stp_x = 0\)

• \(SG(x) = 0\)，必败态，\(stp_x = \min \{stp_y + 1，y \in son_x\}\)

• \(SG(x) \ne 0\)，必胜态，\(stp_x = \max \{stp_y + 1，y \in son_x \& SG(y) = 0\}\)

设 \(step\) 为每个单一游戏的 \(stp\) 的最大值，如果 \(step\) 为奇数，先手必胜。

\(\textup{阶梯 Nim}\)

有这样一种 \(\mathtt{Nim}\) 博弈的变形：

有 \(n\) 层阶梯，第 \(i\) 层上有 \(a_i\) 个石子，每次操作可以选择一层上的若干石子将它们移到下一级，谁最先将石子全部移到第 \(0\) 层谁胜。

先说结论：当 \(a_1 \oplus a_3 \oplus a_5 \oplus ... \oplus a_n = 0\) 时，先手必败，否则必胜。

考虑移动偶数层的影响，假如先手移动了偶数层，则说明这些石子的移动是有必要的，那么后手就可以选择将这些石子移回偶数层，可以保证这一步操作后手是不劣的，则移动偶数层是不优的。

那么原问题就转化成普通 \(\mathtt{Nim}\) 游戏了，移动奇数层石子到偶数层，相当于将石子取走，因为石子没有移动的必要了。

\(\textup{Nim-K}\)

又有这样一种 \(\mathtt{Nim}\) 博弈的变形：

有 \(n\) 堆石子，每堆有 \(a_i\) 个。两人取石子，每人每次选 \(k\) 堆石子，每堆任取石子，取走最后一堆为胜。

结论：当二进制下每一位在 \(a\) 中 \(1\) 的个数都能被 \(k + 1\) 整除时，先手必败。

证明即是将每个 \(a_i\) 拆成二进制看，相当于每次每位最多改变 \(k\) 个 \(1\)，然后按照 \(\mathtt{Nim}\) 博弈的证明思路即可。

但注意一个点，\(k\) 阶情况下，子游戏的 \(\mathtt{SG}\) 函数只能用来分析胜负，并求必胜策略，而不能求出“ \(k\) 阶和游戏”的 \(\mathtt{SG}\) 函数。也就是说，二进制位下分别加和只是得到一组数，而非一个数。所以 \(\mathtt{Nim-K}\) 和 \(k\) 阶 \(\mathtt{SG}\) 不能混为一谈。

\(\textup{树的删边游戏}\)

\(\textup{[AGC017D] Game on Tree}\)

给定一颗树和书的根节点，每次选取一条边删除，然后删除不与根节点联通的连通块，谁删掉最后一条边为胜。

先给结论：叶节点的 \(\mathtt{SG}\) 值为 \(0\)，其余节点 \(u\) 的 \(\mathtt{SG}\) 值为 \(SG_u = \oplus_{v, v \in son_u}(SG_V + 1)\)

考虑证明：

• 叶节点无边可删， \(\mathtt{SG}\) 值为 \(0\)

• 对于节点 \(u\)，假设它只有子节点 \(v\)，删除边 \((u, v)\)，很明显剩下的根节点 \(SG_u = 0\)

• 删除 \(v\) 的其他子树，由于 \(\mathtt{SG}\) 值为 \(\{0, 1, ... SG_{v - 1}\}\) 都出现过，则 \(SG_u\) 归纳为 \(\mathrm{mex}\{1, 2, ... SG_v\}\)。

• \(u\) 有多个子节点，每一个是独立的简单游戏，则 \(SG_u = \oplus_{v, v \in son_u}(SG_V + 1)\)。

\(\textup{局部连通图的删边游戏}\)

这里的局部连通图指图由树加边而成，且没有环有公共边，也就是环是挂在树的某个节点上。

如图

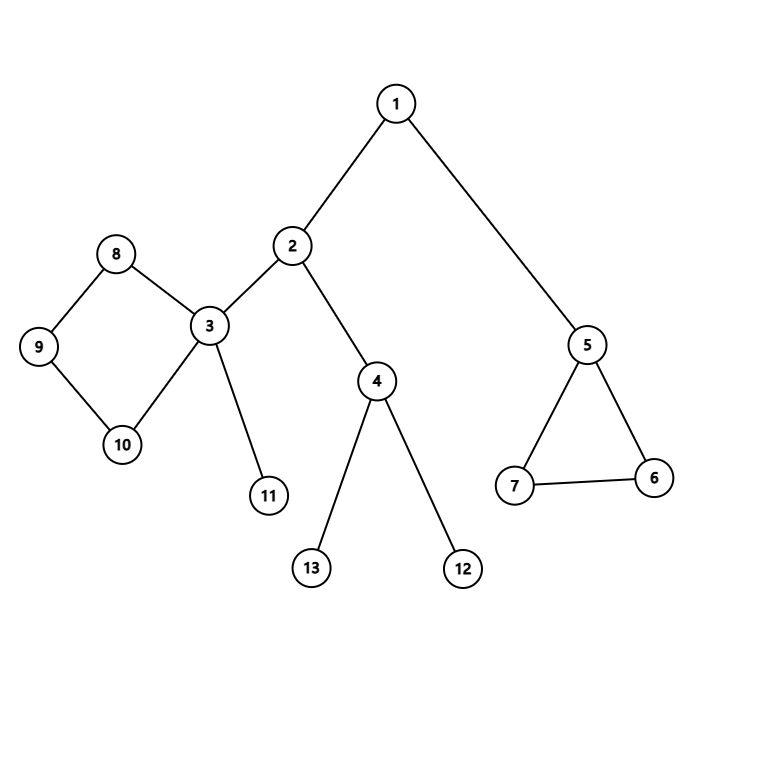
分别考虑每个环。

当断开环上的一条边时，环就转化成了两条链，分别考虑奇环和偶环，断一条边后的两条链分别同奇偶，异奇偶。

同奇偶则代表先手可以划分成长度一样的两条链，异奇偶则是先手被划分成两条一样的链，所以奇环的 \(\mathtt{SG}\) 为 \(1\)，偶环的 \(\mathtt{SG}\) 为 \(0\)。

将每个环看成一条链，原问题转化为树的删边游戏。

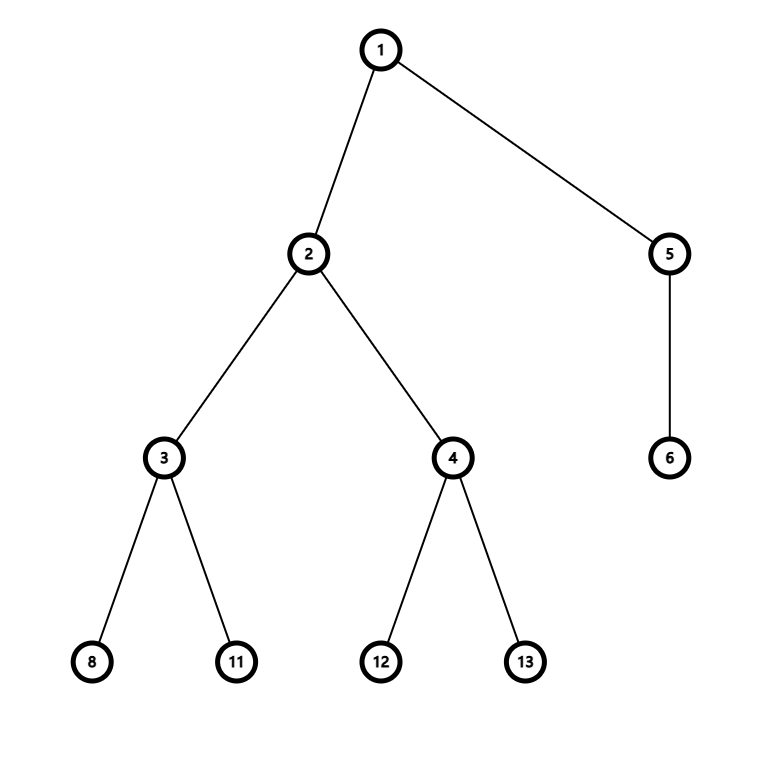
\(\textup{无向图的删边游戏}\)

去除局部连通图的限制，转化为无向图的删边游戏。

给定一个无向图，选定一个根节点，轮流断边，与根节点不连通的部分被删掉，无边可删判负。

• \(\mathtt{Fusion\ Principle}\) ： 对无向图进行如下改动：将途中任意一个偶环缩成一个新点，任意一个奇环缩成一个新点加一个新边；所有连到原先环上的边全部改为与新点相连，这样的改动不会影响图的 \(\mathtt{SG}\) 值。

关于 \(\mathtt{Fusion\ Principle}\) 的证明比较复杂，笔者水平有限，就不发表拙见了。
详细证明参考《Winning Ways for Your Mathematical Plays》系列

通过缩点的操作，原无向图就转化成了树的删边游戏。

\(\textup{例题}\)

\(\textup{[GZOI2017] 取石子游戏}\)

\(\mathtt{tag}\)：\(\mathtt{Nim}\) 博弈

考虑 \(\mathtt{Alice}\) 什么时候必败：

• 选出来的石子堆异或和为 \(0\)，根据 \(\mathtt{Nim}\) 博弈的结论，此时先手必败。

• 选出来的石子堆异或和不为 \(0\)，但指定 \(\mathtt{Alice}\) 选的第一堆选完后不能使石子堆异或和为 \(0\)。

假如选出来的石子堆异或和为 \(A\)，当指定的一堆石子 \(x\) 选完后不能使 \(A\) 变为 \(0\)，那么 \(x < A\)。

观察数据范围，发现值域很有意思，石子数和石子堆数是同阶的，这启发我们将石子数也考虑进状态。

枚举 \(\mathtt{Alice}\) 指定选的石子堆 \(x\)，设 \(f_{i, j}\) 为选了前 \(i\) 堆石子，异或和为 \(j\) 的方案数。

\[f_{i,j} = f_{i - 1, j} + [i \ne x]f_{i - 1, j \oplus a_i} \]

最后答案为 \(\sum_{x \in [1, n]}{\sum_{i\in [a_x,2^8]} {f_{n,i}}}\)

\(\textup{高手过招}\)

\(\mathtt{tag}\)：阶梯 \(\mathtt{Nim}\) 博弈

数据范围很有提示性，\(n \le 20\)，所以直接状压预处理每个状态的 \(\mathtt{SG}\) 值，时间复杂度大约是能过的。

然而这并不优雅，可以再画画图，模拟模拟样例，然后就会发现一个优雅的转化。

由于空格的数量是不变的，我们可以把空格看成台阶，移动棋子就相当于下放台阶，于是原问题就转换为了阶梯 \(\mathtt{Nim}\) 的模板。

这种通过移动交换棋子状态转换为阶梯 \(\mathtt{Nim}\) 博弈的套路挺常见的。

\(\textup{[AGC010F] Tree Game}\)

\(\mathtt{tag}\)：博弈论，贪心

先从简单的问题考虑，假设这棵树是一个菊花图。

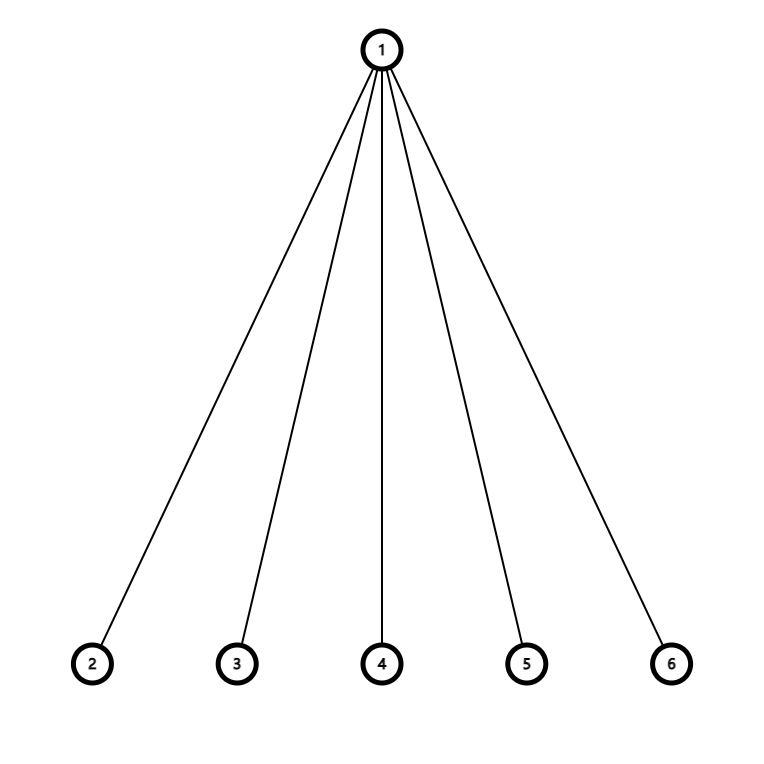
先手将棋子放在 \(1\) 号节点。现在先手要移动棋子到 \(1\) 号节点到相邻的点，由于先手可以将棋子移到任何节点，但后手只能将它移回 \(1\) 号节点，形成了一个循环。而贪心地想，为了保证游戏胜利，也就是将棋子移向没有石子的节点，先手一定只会将棋子移向同一个节点，且这个节点的石子在子节点中最少。那么先手必胜的条件就是 \(1\) 号节点的石子数大于他的子节点中石子数最少的节点的石子数。

现在考虑更一般的情况。

先手依然将棋子放在 \(1\) 号节点。依然贪心地想，假如先手将棋子移向了一个先手必胜的点，那么先手就必败了，所以先手只能将棋子移向一个先手必败的子节点。根据菊花的情况，如果先手必败的子节点中石子数的最小值如果小于了根节点，那么此时先手必败，否则必胜。

对于后手还有一种操作就是将被先手移到先手必败的子节点的棋子移回根节点，可以证明这种操作不会改变这个节点的必败态，由于减少的是字数的根节点的石子数，这个节点就更难大于他的子节点的石子数。

\(\textup{[HNOI2007] 分裂游戏}\)

\(\mathtt{tag}\)：\(\mathtt{Multi-SG}\) 博弈

比较简单的 \(\mathtt{Multi-SG}\) 博弈。

首先发现石子数的奇偶性不会影响 \(\mathtt{SG}\) 函数值，后手可以复制先手的操作。

从 \(i\) 中取出一颗石子并在 \(j, k\) 中加入一颗石子，很明显已经明示这是 \(\mathtt{Multi-SG}\) 博弈，而一颗石子只会对其后面的瓶子产生影响，且这个影响跟原来后面瓶子中的石子数没有关系，于是可以分别处理每个瓶子中的石子的 \(\mathtt{SG}\) 值。

具体地，对于每一个瓶子 \(i\)，枚举处于这一个瓶子中的一个石子的后续状态 \(j, k\)，暴力查找 \(\mathtt{mex}\) 更新。

\[sg_i = \mathrm{mex}\{sg_j \oplus sg_k, i < j \le k \le n\} \]

最后的原状态答案就是 \(\oplus_{i, a_i \% 2 = 1} (sg_i)\)

原题还要求找第一步的取法，暴力枚举 \(i, j, k\)，当将 \(i\) 分到 \(j, k\) 后后手必败，也就是异或和为 \(0\)，则说明后手必败，方案可行。

时间复杂度为 $\mathcal{O}(Tn^3) $。

\(\textup{[清华集训2016] Alice 和 Bob 又在玩游戏}\)

\(\mathtt{tag}\)：\(\mathtt{Multi-SG}\) 博弈，\(\mathtt{01 Trie}\)

首先发现一次操作相当于将一个状态分成很多个字数的状态，所以是一个很明显的 \(\mathtt{Multi-SG}\)。

直接算每一个节点剖分后的答案很明显是不现实的，设 \(G(v, u)\) 表示从 \(v\) 到 \(u\) 的节点删掉剩下的子树 \(\mathtt{SG}\) 异或值，那么 \(SG(u) = \mathrm{mex}_{v \in son(u)}{G(u, v),}\)。

考虑如何维护 \(G\)，可以用 \(\mathtt{01 Trie}\) 维护所有 \(G\) 值，更新 \(u\) 的 \(\mathtt{SG}\) 就把子树的 \(\mathtt{Trie}\) 合并，然后在 \(\mathtt{Trie}\) 中找 \(\mathrm{mex}\)，最后全体异或上删除 \(u\) 的子树异或值值，然后插入。