《概率入门》 5.2 极限定理

在本节中，我们简要讨论概率中的两个主要结果：大数定律（Law of Large Numbers LLN）和中心极限定理（Central Limit Theorem CLT）。两者都是关于独立随机变量的总和。
令 \(X_1,X_2,\cdots\) 为独立且同分布的随机变量。对于每个 n

\[S_n=X_1+\cdots+X_n \]

假设 \(\mathbb{E}X_i = μ\) 且 \(Var(X_i) = σ^2\)。我们假设 μ 和 \(σ^2\) 都是有限的。根据期望和方差的规则我们知道

\[\mathbb{E}S_n=n\mathbb{E}X_1=n\mu \]

和

\[Var(S_n)=n~Var(X_1)=n\sigma^2 \]

此外，如果 \(X_i\) 具有矩生成函数 M，则 \(S_n\) 的 MGF 简单定义如下

\[\mathbb{E}e^{e(X_1+\cdots+X_n)}=\mathbb{E}e^{sX_1}\cdots \mathbb{E}e^{sX_n}=[M(s)]^n \]

大数定律粗略地表明，对于较大的 n，\(S_n/n\) 接近 μ。这里有一个更准确的说法。

定理 5.4 ((弱)大数定律)如果 \(X_1,\cdots, X_n\) 独立同分布于期望 μ，则对于所有 \(\epsilon\) > 0

\[\lim_{n \to \infty} \mathbb{P} \left( \left| \frac{S_n}{n} - \mu \right| \geq \epsilon \right) = 0 \]

证明。首先，对于任何 z > 0 和任何正随机变量 Z，我们有

\[\begin{align*} \mathbb{E}Z &= \int_0^z t f(t) \, dt + \int_z^\infty t f(t) \, dt \geq \int_z^\infty t f(t) \, dt \\ &\geq \int_z^\infty z f(t) \, dt = z \mathbb{P}(Z \geq z), \end{align*} \]

由此立即得出如下马尔可夫不等式(Markow inequality)：如果 Z ≥ 0，那么对于所有 z > 0

$\mathbb{P}(Z \geq z) \leq \frac{\mathbb{E}Z}{z}$   (5.14)

现在取 \(Z=(S_n/n−μ)^2\) 且 \(z=\epsilon^2\)。那么，

\[\mathbb{P}(Z^2 \geq \epsilon^2) \leq \frac{\mathbb{E}\left(S_n/n - \mu\right)^2}{\epsilon^2} \]

上式左边的大小也可以写为 \(\mathbb{P}(|S_n/n − μ| ≥ \epsilon)\)，右边等于\(S_n/n\)的方差，即\(σ^2/n\)。结合得到

\[\mathbb{P} \left( \left| S_n/n - \mu \right| \geq \epsilon \right) \leq \frac{\sigma^2}{n \epsilon^2} \]

对于任何 \(\epsilon>0\)。当 n → ∞ 时，商 \(\frac{\sigma^2}{n\epsilon^2}\) 趋于零，因此 \(\mathbb{P}(|S_n/n-\mu|\geq \epsilon)\) 也趋于零，这一点已被证明。

还有一个强大数定律(strong law of large numbers)，它隐含着弱定律，但更难证明。它规定如下：

\[\mathbb{P} \left( \lim_{n \to \infty} \frac{S_n}{n} = \mu \right) = 1 \]

当 n → ∞，意味着结果集 ω 满足 \(\frac{S_(ω)}{n} \to \mu\) 的概率为一。换句话说，如果我们要运行计算机模拟，那么我们模拟的所有路径都会收敛到 μ。

中心极限定理描述了\(S_n\)（或 \(S_n/n\)）的近似分布。大致是这么说的：

大量独立同分布随机变量之和近似服从正态分布

这里有一个更准确的说法。

定理 5.5（中心极限定理 Central Limit Therem） 如果 \(X_1,\cdots, X_n\) 独立同分布，期望为 μ 且方差 \(σ^2 < \infty\)，则对于所有 x ∈ R，

\[\lim_{n \to \infty} \mathbb{P} \left( \frac{S_n - n \mu}{\sigma \sqrt{n}} \leq x \right) = \Phi(x) \]

其中 Φ 是标准正态分布的 cdf

换句话说，\(S_n\) 近似服从正态分布，期望为 nμ，方差为 \(nσ^2\)。

证明。（草图） 一般地假设 μ = 0 且 σ = 1。这相当于用 \((X_n − μ)/σ\) 替换\(X_n\)。 MGF 在 s = 0 附近的泰勒展开式(Taylor-expansion)为

\[M(s) = \mathbb{E} e^{s X_1} = 1 + s \mathbb{E} X_1 + \frac{1}{2} s^2 \mathbb{E} X_1^2 + o(s^2) = 1 + \frac{1}{2} s^2 + o(s^2) \]

其中 o(·) 是 \(lim_{x↓0} o(x)/x = 0\) 的函数。因为 \(X_1, X_2,\cdots\) 独立同分布，因此 $ S_n/\sqrt{n}$ 的 MGF 满足

\[\begin{align*} \mathbb{E} \exp \left( s \frac{S_n}{\sqrt{n}} \right) &= \mathbb{E} \exp \left( \frac{s}{\sqrt{n}} (X_1 + \cdots + X_n) \right) = \prod_{i=1}^n \mathbb{E} \exp \left( \frac{s}{\sqrt{n}} X_i \right) \\ &= M^n \left( \frac{s}{\sqrt{n}} \right) = \left[ 1 + \frac{s^2}{2n} + o\left(\frac{s^2}{n}\right) \right]^n \end{align*} \]

对于 n → ∞，它收敛于\(e^{s^2/2}\)，这是标准正态分布的 MGF。因此，$ S_n/\sqrt{n}$ 的 cdf 收敛于 Φ 是合理的。为了使这一论点严谨，需要证明矩生成函数的收敛意味着 cdf 的收敛。此外，由于对于某些分布，MGF 不存在于 0 邻域内，因此需要用一种更灵活的变换来代替上面论证中的 MGF，即傅立叶变换(Fourier transform)，也称为特征函数(characteristic function)：\(r \mapsto \mathbb{E}e^{irX} , r \in R\)。

要了解 CLT 的实际情况，请考虑图 5.4。第一张图片显示了具有 U[0, 1] 分布的 \(X_i\) 的 pdf 的 \(S_1,\cdots,S_4\)。第二个显示了 Exp(1) 分布相同情况，我们清楚地看到收敛到钟形曲线

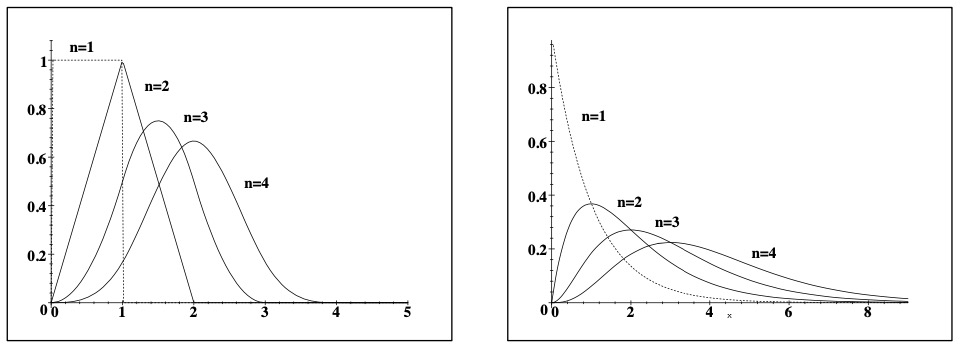
图 5.4：均匀分布和指数分布的 CLT 图

CLT 不限于连续分布。例如，图 5.5 显示了成功概率为 1/2 的伯努利分布的 $X_i$ 的 cdf $S_{30}$。注意$S_{30}$ ∼ Bin(30, 1/2)，参见例 4.3。

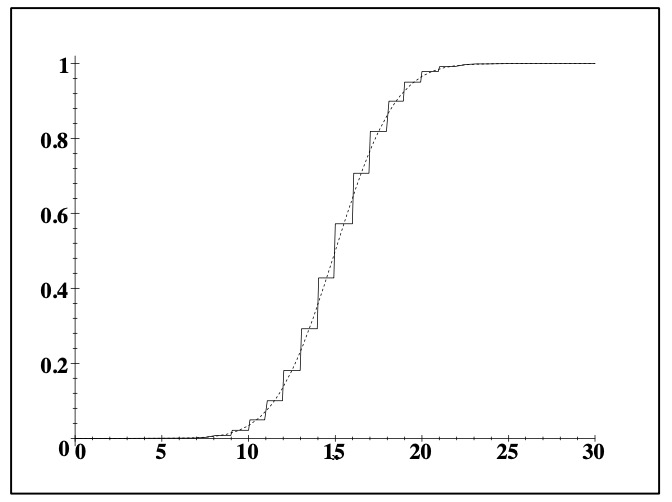
图 5.5：Bin(20, 1/2) 分布的 cdf 及其正态近似

一般来说，我们得到：

定理 5.6 令 X ∼ Bin(n, p)。对于大 n 我们得到

\[\mathbb{P}(X \leq k)\approx \mathbb{P}(Y\leq k) \]

其中 Y ∼ N(np,np(1−p)) 。根据经验，如果 np 和 n(1 − p) 都大于 5，则近似是准确的。