《概率入门 随机变量函数和极限定理》 5.1 联合正态随机变量

假设 \(X_1,\cdots,X_n\) 是随机实验的测量值。通常我们只对测量的某些功能感兴趣，而不是所有测量本身。例如，如果 \(X_1,\cdots,X_n\) 是某种类型钓鱼线强度的重复测量值，那么我们真正感兴趣的不是 \(X_1,\cdots,X_n\) 的各个值而是数量，如平均强度 (\(X_1,\cdots,X_n\))/n、最小强度 min(\(X_1,\cdots,X_n\)) 和最大强度 max(\(X_1,\cdots,X_n\)) 。请注意，这些数量又是随机变量。这些随机变量的分布原则上可以从 \(X_i\) 的联合分布中推导出来。我们举了很多例子。

示例 5.1 设 X 为具有 pdf \(f_X\) 的连续随机变量，并设 Y =aX+b，其中 \(a \neq 0\)。我们希望确定 Y 的 pdf \(f_Y\)。我们首先用 X 的 cdf 来表示 Y 的 cdf。首先假设 a > 0。对于任何 y，我们有

\[F_Y(y)=\mathbb{P}(Y\leq y)=\mathbb{P}(X\leq(y-b)/a)=F_X((y-b)/a) \]

对 y 求导我们得到 \(f_Y(y)=f_X((y-b)/a)/a\)。对于所有 a < 0 我们类似得到 \(f_Y(y)=f_X((y-b)/a)/(-a)\)，因此一般来说

$f_Y(y)=\frac{1}{|a|}f_X\left(\frac{y-b}{a}\right)$  (5.1)

示例 5.2 令 X ∼ N(0, 1)。我们希望确定 \(Y=X^2\) 的分布。我们可以使用与上例相同的技术，但首先请注意，Y 只能取 [0, ∞) 中的值。对于 y > 0 我们有

\[\begin{align*} F_Y(y)&=\mathbb{P}(Y\leq y)=\mathbb{P}(-\sqrt y \leq X \leq \sqrt y) \\ &=F_X(\sqrt y)-F_X(-\sqrt y)=2F_X(\sqrt y) -1 \end{align*} \]

对 y 求导我们得出

\[\begin{align*} f_Y(y)&=2f_X(\sqrt y)\frac{1}{2\sqrt y}=\frac{1}{\sqrt{2 \pi}}exp\left(-\frac{1}{2}(\sqrt y)^2\right)\frac{1}{\sqrt y} \\ &=\frac{(1/2)^{1/2}y^{-1/2}e^{-y/2}}{Γ(1/2)} \end{align*} \]

这正是卡方分布(\(χ_1^2\)-distribution)的 pdf 公式。因此\(Y \sim χ_1^2\)

示例 5.3（最小值和最大值）假设 \(X_1,\cdots,X_n\) 是独立的并且有 cdf F。令 Y = min(\(X_1,\cdots,X_n\)) 且 Z = max(\(X_1,\cdots,X_n\))。 Y和Z的cdf很容易获得。首先，请注意，当且仅当所有 \(X_i\) 都小于 z 时，{\(X_i\)} 的最大值才小于某个数字 Z。因此，

\[\mathbb{P}(Z \leq z)=\mathbb{P}(X_1 \leq z,X_2\leq z,\cdots,X_n\leq z)=\mathbb{P}(X_1\leq z)\mathbb{P}(X_2\leq z)\cdots \mathbb{P}(X_n\leq z) \]

其中第二个方程是根据独立性假设得出的。由此可见

\[F_Z(z)=(F(z))^n \]

类似的，

\[\mathbb{P}(Y>y)=\mathbb{P}(X_1>y,X_2>y,\cdots,X_n>y)=\mathbb{P}(X_1>y)\mathbb{P}(X_2>y)\cdots \mathbb{P}(X_n>y) \]

因此

\[F_Y(y)=1-(1-F(y))^n \]

示例5.4 在第3章中，我们看到了随机变量函数的一个重要应用：生成随机变量的逆变换方法。即 U ∼ U(0, 1)， F 为连续且严格递增 cdf。那么 \(Y=F^{-1}(U)\) 是一个具有 cdf F 的随机变量。

我们可以使用模拟来了解一个或多个随机变量的函数的分布，如以下示例中所述。

示例 5.5 设 X 和 Y 独立且 U(0,1) 均分布。 Z = X + Y 的 pdf 是什么样的？请注意，Z 取 (0,2) 中的值。下面的 matlab 线从 Z 的分布中绘制 10,000 次，并绘制数据的直方图（图 5.1）

hist(rand(1,10000)+rand(1,10000),50)

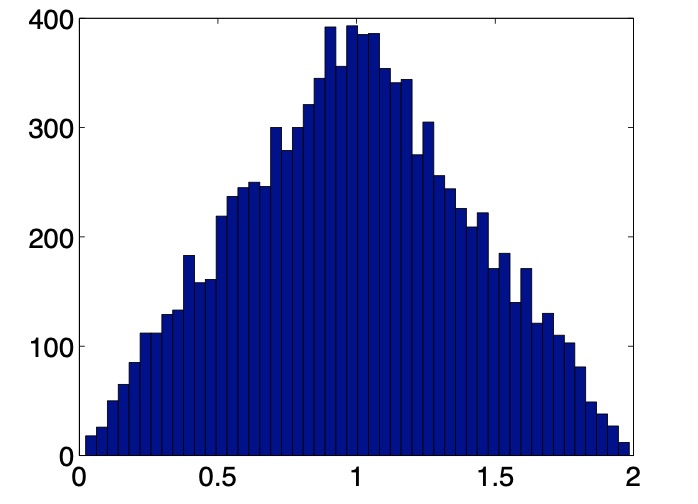
图 5.1 添加两个均匀随机变量的直方图

这看起来非常像一个三角形。也许 Z = X + Y 的真实 pdf 具有三角形形状？这确实很容易证明。也就是说，首先观察到 Z 的 pdf 必须围绕 1 对称。因此，要找到 pdf，只需找到 z ∈ [0, 1] 的形式即可。取这样一个z。然后，见图5.2，

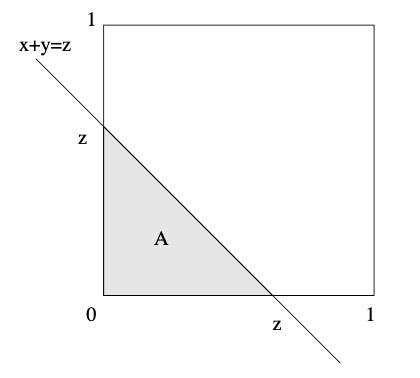
图 5.2：随机点 (X, Y ) 一定位于集合 A 中

$$ F_Z(z)=\mathbb{P}(Z\leq z)=\mathbb{P}((X,Y) \in A)=\int \int_Af(x,y)~dxdy=area(A)=\frac{1}{2}z^2 $$ 其中使用了正方形 [0, 1] × [0, 1] 上的联合密度 f(x,y) 等于 1 的事实。通过对 cdf $F_Z$ 求导，我们得到 pdf $f_Z$ $$ f_Z(z)=z,~z \in [0,1] $$ 并通过对称性 $$ f_Z(z)=2-z,~z \in [1,2] $$ 这确实是一个三角形密度。如果我们重新调整直方图的比例，使条形图下方的总面积为 1，则与真实分布的拟合将会非常好。

线性变换(Linear Transformations)

令 \(\mathbf{x}=(x_1,\cdots,x_n)^T\) 为 \(\mathbb{R}^n\) 中的（列）向量，A 为 (n × m) 矩阵。映射 x → z，其中

\[\mathbf{z}=A\mathbf{x} \]

被称为线性变换。现在考虑一个线性向量 \(\mathbf{X}=(X_1,\cdots,X_n)^T\)，并且令

\[\mathbf{Z}=A\mathbf{X} \]

那么 \(\mathbf{Z}\) 是 \(\mathbb{R}^m\) 中的随机向量。同样，原则上，如果我们知道 \(\mathbf{X}\) 的联合分布，那么我们就可以推导出 \(\mathbf{Z}\) 的联合分布。首先让我们看看期望向量和协方差矩阵是如何变换的。

定理 5.1 如果 X 具有期望向量 \(\mu_X\) 和协方差矩阵 \(\Sigma_X\)，则 \(\mathbf{Z}=A\mathbf{X}\) 的期望向量和协方差矩阵分别为

$\mathbf{\mu}_Z=A\mathbf{\mu}_X$    (5.2)

和

$\Sigma_Z=A\Sigma_XA^T$    (5.3)

证明。我们有 $\mu_Z=\mathbb{E}Z=\mathbb{E}A\mathbf{X}=A\mu_\mathbf{X}$ 和 $$ \begin{align*} \Sigma_{\mathbf{Z}}&=\mathbb{E}(\mathbf{Z}-\mu_{\mathbf{Z}})(\mathbf{Z}-\mu_{\mathbf{Z}})^T=\mathbb{E}A(\mathbf{X}-\mu_{\mathbf{X}})(A(\mathbf{X}-\mu_{\mathbf{X}}))^T \\ &=A\mathbb{E}(\mathbf{X}-\mu_{\mathbf{X}})(\mathbf{X}-\mu_{\mathbf{X}})^TA^T \\ &=A\Sigma_{\mathbf{X}}A^T \end{align*} $$ 由此完全可以证明。

从现在开始假设 A 是可逆 (n×n)−矩阵。如果 X 的联合密度为 \(f_\mathbf{X}\)，那么 Z 的联合密度 \(f_\mathbf{Z}\) 是多少？

考虑图 5.3。对于任何固定的 x，令 z = Ax。因此，\(\mathbf{x}=A^{-1}\mathbf{z}\)。考虑 n 维立方体 \(C=[z_1,z_1+h] \times \cdots \times[z_n,z_n+h]\)。令 D 为 C 在 \(A^{-1}\) 下的图，例如平行六面体(parallelepiped)的所有点 x ，存在 \(A\mathbf{x} \in C\)。那么，

\[\mathbb{P}(\mathbf{Z} \in C) \approx h^nf_Z(\mathbf{z}) \]

现在回想一下线性代数，任何具有“体积”V 的 n 维矩形都可以转化为具有体积 V |A| 的 n 维平行六面体，其中 |A| := |det(A)|。因此，

\[\mathbb{P}(\mathbf{Z} \in C) =\mathbb{P}(\mathbf{X} \in D) \approx h^n|A^{-1}|f_X(x)=h^n|A|^{-1}f_X(x) \]

令 h 趋近于 0 我们得出

$f_Z(z)=\frac{f_X(A^{-1}\mathbf{z})}{|A|}, \mathbf{z} \in \mathbb{R}^n$  (5.4)

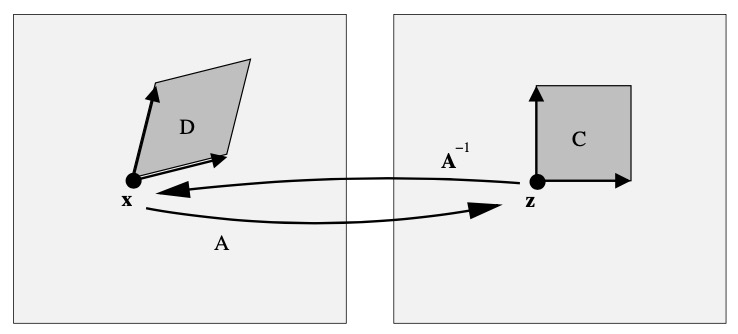
图 5.3 线性转换

一般转换

我们可以将线性转换技术应用于一般转换 \(\mathbf{x}\mapsto \mathbf{g}(\mathbf{x})\)，写出：

\[\begin{pmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{pmatrix} \mapsto \begin{pmatrix} g_1(\mathbf{x}) \\ g_2(\mathbf{x}) \\ \vdots \\ g_n(\mathbf{x}) \end{pmatrix} \]

对于固定的 \(\mathbf{x}\)，令 \(\mathbf{z}=\mathbf{g}(\mathbf{x})\)。假设 \(\mathbf{g}\) 是可逆的，那么 \(\mathbf{x}=\mathbf{g}^{-1}(\mathbf{z})\)。任何位于 \(\mathbf{x}\) 体积为 V 的无穷小 n 维矩形可以转换为位于 \(\mathbf{z}\)，体积为 \(V|J_{\mathbf{x}}(\mathbf{g})|\) 的n 维平行六面体，其中 \(J_{\mathbf{x}}(\mathbf{g})\) 是转换 \(\mathbf{g}\) 在 \(\mathbf{x}\) 处的雅可比矩阵(matrix of Jacobi)：

\[\begin{align*} J_{\mathbf{x}}(\mathbf{g}) = \begin{bmatrix} \frac{\partial g_1}{\partial x_1} & \cdots & \frac{\partial g_1}{\partial x_n} \\ \vdots & \cdots & \vdots \\ \frac{\partial g_n}{\partial x_1} & \cdots & \frac{\partial g_n}{\partial x_n} \end{bmatrix} \end{align*} \]

现在考虑一个随机列向量 \(\mathbf{Z}=\mathbf{g}(\mathbf{X})\)。令 C 为围绕 z 的小立方体，体积为 \(h^n\)。令 D 为 C 在 \(g^{-1}\) 下的图。然后，与线性情况一样，

\[\mathbb{P}(\mathbf{Z} \in C) \approx h^n~f_\mathbf{Z}(\mathbf{z}) \approx h^n|J_\mathbf{z}(\mathbf{g}^{-1})|f_\mathbf{X}(\mathbf{x}) \]

因此，我们得到转换法则

\[f_\mathbf{Z}(\mathbf{z})=f_\mathbf{X}(\mathbf{g}^{-1}(\mathbf{z}))|J_\mathbf{z}(\mathbf{g}^{-1})|,\mathbf{z} \in \mathbb{R}^n \]

(请注意：\(|J_\mathbf{z}(\mathbf{g}^{-1})|=1/|J_\mathbf{x}(\mathbf{g})|\))

备注 5.1 在大多数坐标变换中，给出的是 \(\mathbf{g}^{-1}\)——即 \(\mathbf{x}\) 作为 \(\mathbf{z}\) 的函数的表达式——而不是 \(\mathbf{g}\)。

示例 5.6 (Box-Muller) 令 X 和 Y 为两个独立的标准正态随机变量。 (X, Y ) 是平面上的随机点。设(R,\(\Theta\))为相应的极坐标。 R 和 \(\Theta\) 的联合 pdf \(f_{R,\Theta}\) 如下

\[f_{R, \Theta}(r, \theta) = \frac{1}{2\pi} e^{-r^2 / 2} r, \quad \text{对于 } r \geq 0 \text{ 且 } \theta \in [0, 2\pi) \]

即，根据 r 和 θ 指定 x 和 y 得到

$x = r~cos\theta\text{ 且 } y=r~sin\theta$  (5.6)

该坐标变换的雅可比行列式(Jacobian)是 $$ \det \begin{bmatrix} \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \theta} \\ \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \theta} \end{bmatrix} = \begin{vmatrix} \cos \theta & -r \sin \theta \\ \sin \theta & r \cos \theta \end{vmatrix} = r $$ 现在的结果来自转换规则 (5.5)，注意到 X 和 Y 的联合 pdf 为 $f_{X,Y}(x,y)=\frac{1}{2\pi}e^{-(x^2+y^2)/2}$。不难验证 R 和 $\Theta$ 是独立的，即 $\Theta$ ∼ U[0, 2π) 且 $\mathbb{P}(R>r)=e^{-r^2/2}$。这意味着 R 与 $\sqrt V$ 具有相同的分布，其中 V～Exp(1/2)。即$\mathbb{P}(\sqrt V>v)=\mathbb{P}(V>v^2)=e^{-v^2/2}$。 θ 和 R 都很容易生成，并通过（5.6）转换为独立的标准正态随机变量。

5.1 联合正态随机变量

在本节中，我们将仔细研究正态分布的随机变量及其属性。此外，我们还将介绍正态分布的随机向量。

将正态分布随机变量视为标准正态随机变量的简单变换是有帮助的。例如，令 X ∼ N(0, 1)。那么，X 的密度 \(f_X\) 由如下

\[f_X(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}} \]

现在考虑转换

\[Z=\mu +\sigma X \]

那么，根据(5.1) Z 有密度

\[f_Z(z)=\frac{1}{\sqrt{2\pi \sigma^2}}e^{-\frac{(z-\mu)^2}{2\sigma^2}} \]

换句话说，\(Z \sim N(\mu,\sigma^2)\)。我们也可以这样写，如果 \(Z ∼ N(μ, σ^2)\)，那么 \((Z-\mu)/\sigma \sim N(0,1)\)。该标准化(standardisation)过程已在第 2.6.3 节中提到。

让我们将其推广到 n 维。令 \(X_1,\cdots,X_n\) 为独立的标准正态随机变量。\(X=(X_1,\cdots,X_n)^T\) 的联合 pdf 如下

$f_\mathbf{X}(\mathbf{x})=(2\pi)^{-n/2}e^{-\frac{1}{2}\mathbf{x}^T\mathbf{x}},~\mathbf{x}\in \mathbb{R}^n$    (5.7)

考虑转换

$\mathbf{Z}=\mathbf{\mu}+B\mathbf{X}$    (5.8)

对于某些 (m×n) 矩阵 B。请注意，根据定理 5.1，Z 具有期望向量 μ 和协方差矩阵 $\Sigma=BB^T$ 。任何 (5.8) 形式的随机向量都被认为具有联合正态（或多变量正态）分布。我们写作 Z ∼ N(μ, Σ)。

假设 B 是可逆 (n × n) 矩阵。然后，根据 (5.4)，Y = Z − μ 的密度如下

\[f_\mathbf{Y}(\mathbf{y})=\frac{1}{|B|=\sqrt{(2\pi)^n}}e^{-\frac{1}{2}(B^{-1}\mathbf{y})^TB^{-1}\mathbf{y}}=\frac{1}{|B|\sqrt{(2\pi)^n}}e^{-\frac{1}{2}\mathbf{y}^T(B^{-1)^T}B^{-1}}\mathbf{y} \]

我们有 \(|B| = \sqrt{|Σ|}\) 且 \((B^{-1})^TB^{-1}=(B^T)^{-1}B^{-1}=(BB^T)^{-1}=\Sigma^{-1}\)，因此

\[f_\mathbf{Y}(\mathbf{y})=\frac{1}{\sqrt{(2\pi)^n|\Sigma|}}e^{-\frac{1}{2}\mathbf{y}^T\Sigma^{-1}\mathbf{y}} \]

因为 Z 是通过 Y 简单地添加一个常数向量 μ 获得，我们有 \(f_\mathbf{Z}(\mathbf{z})=f_\mathbf{Y}(\mathbf{z}-\mu)\)，因此

$f_\mathbf{z}(\mathbf{z})=\frac{1}{\sqrt{(2\pi)^n|\Sigma|}}e^{-\frac{1}{2}(\mathbf{z}-\mu)^T\Sigma^{-1}(\mathbf{z}-\mu)},\mathbf{z}\in\mathbb{R}^n$  (5.9)

请注意，该公式与一维情况非常相似。

示例 5.7 考虑 \(\mathbf{μ} = (μ_1, μ_2)^T\) 的二维情况，并且

$B = \begin{pmatrix} \sigma_1 & 0 \\ \sigma_2 \rho & \sigma_2 \sqrt{1 - \rho^2} \end{pmatrix}$  (5.10)

现在协方差矩阵是

$\Sigma = \begin{pmatrix} \sigma_1^2 & \rho \sigma_1 \sigma_2 \\ \rho \sigma_1 \sigma_2 & \sigma_2^2 \end{pmatrix}$  (5.11)

因此，密度为

$f_z(z) = \frac{1}{2 \pi \sigma_1 \sigma_2 \sqrt{1 - \rho^2}} \exp \left\{ - \frac{1}{2(1 - \rho^2)} \left( \frac{(z_1 - \mu_1)^2}{\sigma_1^2} - 2\rho \frac{(z_1 - \mu_1)(z_2 - \mu_2)}{\sigma_1 \sigma_2} + \frac{(z_2 - \mu_2)^2}{\sigma_2^2} \right) \right\}$  (5.12)

这是密度的一些图片，对于 和，以及不同的 ρ。

我们说 $(Z_1 , Z_2 )^T$ 具有二元正态(bivariate normal)分布。请注意，在此示例中 $\mathbb{E}Z_i=\mu_i,~i=1,2$。此外，由于我们选择了 B，使得协方差矩阵具有 (5.11) 的形式，因此我们有 $Var(Z_i) = σ_i^2,~i = 1,2$，并且 $ρ(Z_1,Z_2) = ρ$。我们很快就会看到 $Z_1$ 和 $Z_2$ 都服从正态分布。

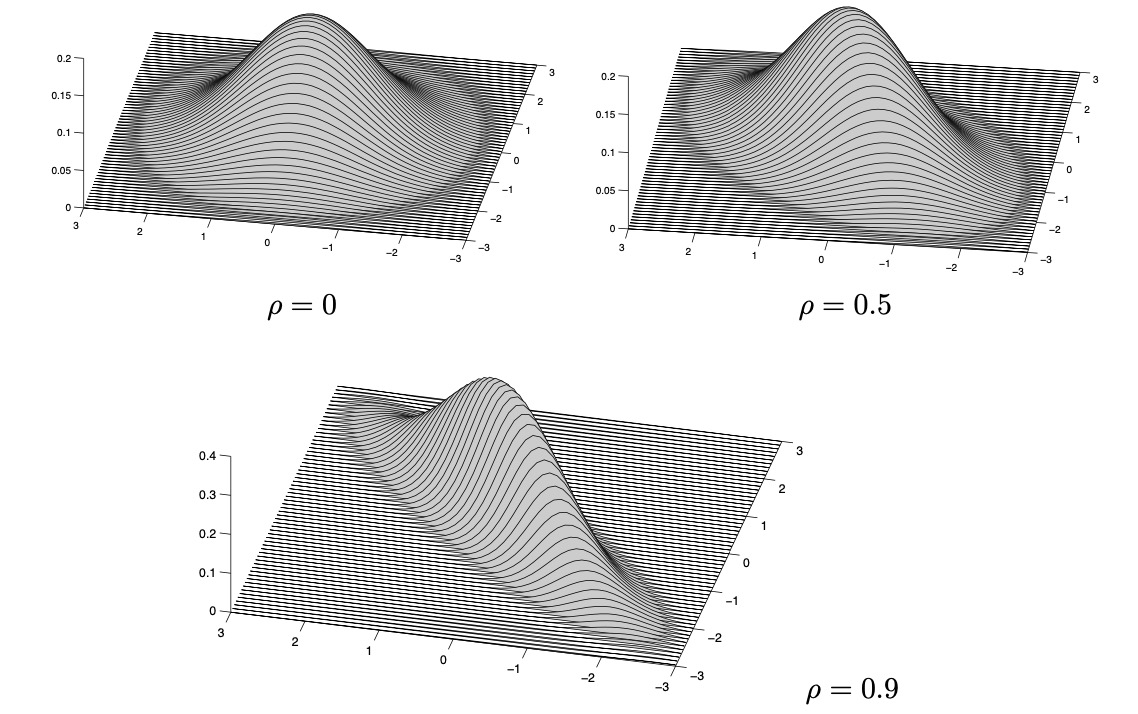
将以下内容与表 4.1 的属性 8 进行比较。

定理 5.2 如果 \(Z_1\) 和 \(Z_2\) 满足联合正态分布，则

\[Cov(Z_1, Z_2) = 0 ⇒ Z_1 ~ Z_2 \text{ 相互独立} \]

证明。如果\(Cov(Z_1 , Z_2 ) = 0\)，则 (5.10) 中的 B 是对角矩阵(diagonal matrix)。因此，简单地说，\(Z_1 = σ_1X_1\) 和 \(Z_2 = σ_2X_2\) 是独立的。
正态分布最（也许不是最）重要的属性之一是独立正态随机变量的线性组合呈正态分布。这里有一个更精确的表述。

定理 5.3 如果 \(X_i ∼ N(μ_i, σ_i^2)\) 对于 i = 1, 2, … , n 独立，那么

$Y=a+\sum_{i=1}^nb_iX_i \sim N \left(a+\sum_{i=1}^nb_i\mu_i,\sum_{i=1}^nb_i^2\sigma_i^2\right)$  (5.13)

证明。证明这一点的最简单方法是使用矩生成函数。首先，回想一下 $N(μ, σ^2)$ 分布的随机变量 X 的 MGF 如下 $$ M_X(s)=e^{\mu s+\frac{1}{2}\sigma^2s^2} $$ 令 $M_Y$ 为 Y 的矩生成函数。因为 $X_1,\cdots,X_n$ 是独立的，我们得出 $$ \begin{align*} M_Y(s) &= \mathbb{E} \exp \left\{ as + \sum_{i=1}^n b_i X_i s \right\} \\ &= e^{as} \prod_{i=1}^n M_{X_i}(b_i s) \\ &= e^{as} \prod_{i=1}^n \exp \left\{ \mu_i (b_i s) + \frac{1}{2} \sigma_i^2 (b_i s)^2 \right\} \\ &= \exp \left\{ sa + s \sum_{i=1}^n b_i \mu_i + \frac{1}{2} \sum_{i=1}^n b_i^2 \sigma_i^2 s^2 \right\} \end{align*} $$ 这里正态分布的 MGF 来自(5.13)

备注 5.2 请注意，根据定理 4.3 和 4.6，我们已经在 (5.13) 中建立了 Y 的期望和方差。但现在我们发现分布是正态的。

示例 5.8 一台机器生产直径为 N(1, 0.01)（厘米）的滚珠轴承。将滚珠放在直径为 N(1.1, 0.04) 的筛子上。假设球和筛子的直径彼此独立。
问题：球掉下来的概率是多少？
答案：设 X ∼ N(1, 0.01) 和 Y ∼ N(1.1, 0.04)。我们需要计算 P(Y >X)=P(Y −X>0)。但是，Z:=Y − X ∼ N(0.1,0.05)。因此

\[\mathbb{P}(Z>0)=\mathbb{P}\left(\frac{Z-0.1}{\sqrt{0.05}}>\frac{-0.1}{\sqrt{0.05}}\right)=Φ(0.447)\approx 0.67 \]

这里Φ是 N(0,1) 分布的 cdf。