《概率分布》2.5 一些重要的离散分布

在本节中，我们给出许多重要的离散分布并列出了它们的一些属性。请注意，每个分布的 pmf 取决于一个或多个参数；所以实际上我们正在处理分布系列。

2.5.1 伯努利分布(Bernoulli Distribution)

如果 X 只能取值 0 和 1，则我们说 X 成功的概率 p 具有伯努利分布，概率为

\[\mathbb{P}(X=1)=p=1-\mathbb{P}(X=0) \]

我们写作 X ∼ Ber(p)。尽管很简单，但这是概率中最重要的分布之一！它模拟了一次抛硬币实验。 cdf 如图 2.5 所示。


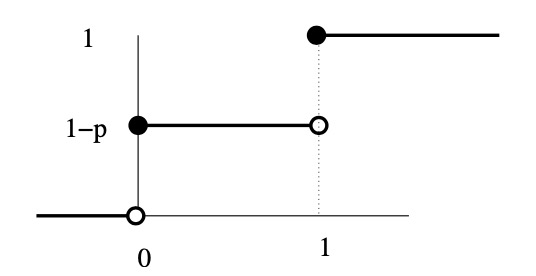
图 2.5 伯努利分布的 cdf

这里有一些属性
  1. 期望是 \(\mathbb{E}X = 0\mathbb{P}(X=0)+1\mathbb{P}(X=1)=0\times(1-p)+1 \times p=p\)
  2. 方差是\(Var(X)=\mathbb{E}X^2-(\mathbb{E}X)^2=\mathbb{E}X-(\mathbb{E}X)^2=p-p^2=p(1-p)\)。（注意 \(X^2=X\)）
  3. PGF 定义为 \(G(z)=z^0(1-p)+z^1p=1-p+zp\)。

2.5.2 二项式分布(Binomial Distribution)

考虑 n 次抛硬币的序列。如果 X 是记录正面总数的随机变量，且“正面”的概率为 p，则我们称 X 具有参数为 n 和 p 的二项式分布，写作X ∼ Bin(n, p)。概率质量函数 X 为：

$f(x)=\mathbb{P}(X=x)=\binom{n}{x}p^x(1-p)^{n-x}, x=0,1,\cdots ,n$    (2.4)

这是从示例 1.15 和 2.2 得出的。图 2.6 给出了 pmf 图表的示例。


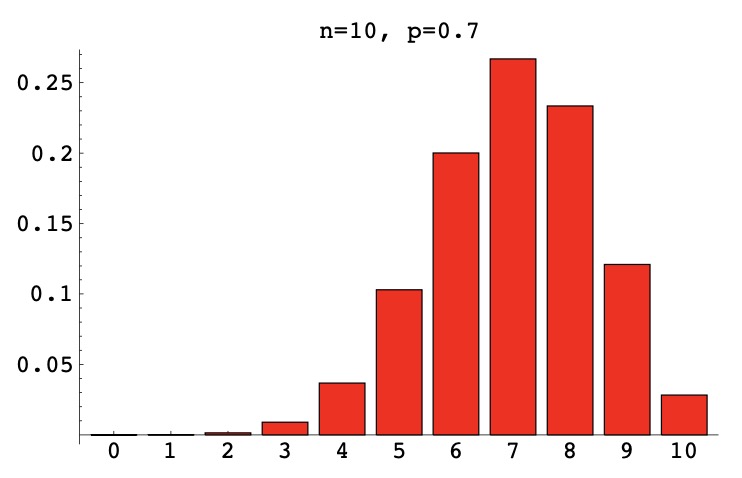
图 2.6 Bin(10,0.7)分布的pmf

以下是二项式分布的一些重要属性。在我们讨论了多个随机变量之后，其中一些属性可以更容易地证明。
  1. 期望是 \(\mathbb{E}X=np\)。这是一个非常直观的结果。如果 p 表示任意一次抛硬币的成功概率，则 n 次抛硬币的期望成功次数（正面）为 np。为了证明这一点，我们可以简单地计算总和

\[\sum_{x=0}^n\binom{n}{x}p^x(1-p)^{n-x} \]

但这并不优雅。我们将在第 4 章中看到，X 可以看作是 n 个独立 Ber(p) 随机变量的和 \(X=X_1+\cdots +X_n\)，其中 \(X_i\) 表示第 i 次抛掷是否成功，\(i=1,\cdots ,n\)。我们还将证明这样一个总和的期望是期望的总和，因此，

\[\mathbb{E}X = \mathbb{E}(X_1 + \cdots + X_n) = \mathbb{E}X_1 + \cdots + \mathbb{E}X_n = \underbrace{p + \cdots + p}_{n \text{ times}} = np \]

  1. X的方差是 Var(X) = np(1-p)。证明的方式与期望相似：

\[\begin{align*} Var(X)&=Var(X_1+\cdots +X_n)=Var(X_1)+\cdots +Var(X_n) \\ &= \underbrace{p(1-p)+ \cdots +p(1-p)}_{n \text{ times}}=np(1-p) \end{align*} \]

  1. X 的概率生成函数为 \(G(z)=(1-p+zp)^n\)。同样，在第 4 章中考虑多个随机变量后，我们可以轻松证明这一点。即，

\[\begin{align*} G(z)&=\mathbb{E}z^X=\mathbb{E}z^{X_1+\cdots +X_n}=\mathbb{E}z^{X_1} \cdots \mathbb{E}z^{X_n} \\ &= (1-p+zp) \times \cdots \times (1-p+zp)=(1-p+zp)^n \end{align*} \]

然而，我们也可以使用牛顿二项式公式轻松证明它：

\[(a+b)^n=\sum_{k=0}^n \binom{n}{k}a^kb^{n-k} \]

具体来说，

\[G(z)=\sum_{k=0}^nz^k\binom{n}{k}p^k(1-p)^{n-k}=\sum_{k=0}^n\binom{n}{k}(zp)^k(1-p)^{n-k}=(1-p+zp)^n \]

请注意，一旦我们获得了 PGF，我们就可以获得期望和方差 G′(1) = np 和 \(G''(1)+G'(1)-(G'(1))^2=(n-1)np^2+np-n^2p^2=np(1-p)\)。

2.5.3 几何分布(Geometric distribution)

我们再次观察抛硬币的序列，但计算不同的东西。令 X 为第一次正面出现前所需的抛掷次数。然后

$\mathbb{P}(X=x)=(1-p)^{x-1}p,x=1,2,3,\cdots$  (2.5)

因为唯一所需要的序列形式为 $$\underbrace {ttt \cdots t}_{x-1}h$$ 其概率为 $(1-p)^{x-1}p$。另请参见1.6.3小节的示例 1.16。这样的随机变量 X 被称为具有参数 p 的几何分布。我们写作 X ∼ G(p)。图 2.7 给出了 pdf 图形的示例


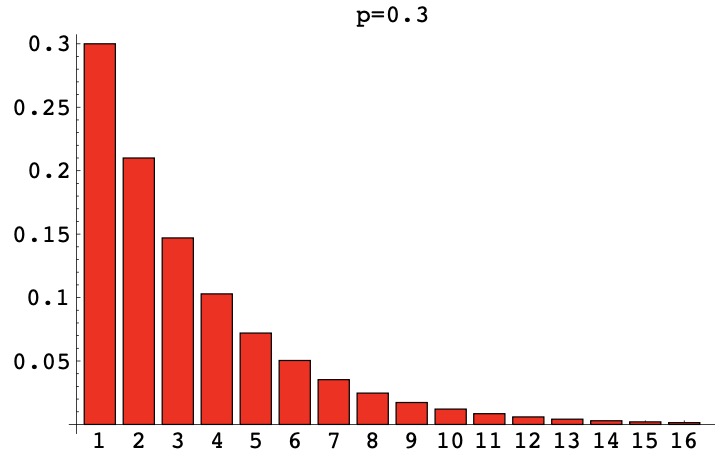
图 2.7 G(0.3)分布的pmf

我们给出了更多的属性，包括几何分布的期望、方差和 PGF。从 PGF 开始是最简单的：
  1. PGF为

\[G(z)=\sum_{x=1}^\infty z^xp(1-p)^{x-1}=zp\sum_{k-0}^\infty(z(1-p))^k=\frac{zp}{1-z(1-p)} \]

根据总所周知的几何求和(geometric sums)：\(1+a+a^2+\cdots = \frac{1}{1-a},|a|< 1\)

  1. 因此期望为 \(\mathbb{E}X=G'(1)=\frac{1}{p}\)
    这是一个直观的结果。如果成功概率为 p，我们预计在成功出现之前等待 1/p 次抛出。

  2. 通过对 PGF 进行两次微分，我们可以得到方差：

\[Var(X)=G''(1)+G'(1)-(G''(1))^2=\frac{2(1-p)}{p^2}+\frac{1}{p}-\frac{1}{p^2}=\frac{1-p}{p^2} \]

  1. 需要超过 k 次抛掷才能成功的概率为 \(\mathbb{P}(X>k)=(1-p)^k\)
    从 {X > k} 对应于 k 次连续失败的事件这一事实可以看出这一点。

几何分布的最后一个值得特别关注的属性是无记忆属性(mempryless property)。再想想抛硬币实验。假设我们已经抛了 k 次硬币，但没有成功（正面）。在成功之前我们需要多于 x 次额外的抛掷的概率是多少？显然，答案与从头开始时需要超过 x 次抛掷的概率相同，即\(\mathbb{P}(X>x)=(1-p)^x\)，与 k 无关。我们已经经历过 k 次失败的事实并不意味着在下一次试验中获得成功的可能性更大。换句话说，硬币对所发生的事情没有记忆，因此称为“无记忆属性”。从数学上讲，这意味着对于任何,

\[\mathbb{P}(X>k+x|X>k)=\mathbb{P}(X>x) \]

证明。根据条件概率的定义

\[\mathbb{P}(X>k+x|X>k)=\frac{\mathbb{P}(\{X>k+x\}\cap\{X>k\})}{\mathbb{P}(X>k)} \]

现在，事件 {X > k + x} 是 {X > k} 的子集，因此它们的交集是 {X > k + x}。此外，事件 {X > k + x} 和 {X > k} 的概率分别为 \((1-p)^{k+x}\) 和 \((1-p)^k\)，因此可证

\[\mathbb{P}(X>k+x|X>k)=\frac{(1-p)^{k+x}}{(1-p)^k}=(1-p)^x=\mathbb{P}(X>x) \]

2.5.4 泊松分布(Poisson Distribution)

随机变量X满足

$\mathbb{P}(X=x)= \frac{\lambda ^x}{x!}e^{-\lambda}, x= 0,1,2, \cdots$   (2.6)

对于固定 λ > 0）则说 X 具有泊松分布。我们写作X～Poi(λ)。泊松分布用于许多概率模型中，并且可以在以下情况被视为大 n 时 Bin(n, μ/n) 的“极限”：考虑一个抛硬币实验，其中我们成功抛硬币 n 次概率 λ/n。令 X 为成功次数。然后，正如我们所见，X ∼ Bin(n, λ/n)。换句话说，

\[\begin{align*} \mathbb{P}(X = k) &= \binom{n}{k} \left( \frac{\lambda}{n} \right)^k \left( 1 - \frac{\lambda}{n} \right)^{n-k} \\ &= \frac{\lambda^k}{k!} \frac{n \times (n-1) \times \cdots \times (n-k+1)}{n \times n \times \cdots \times n} \left( 1 - \frac{\lambda}{n} \right)^n \left( 1 - \frac{\lambda}{n} \right)^{-k} \end{align*} \]

当 n → ∞ 时，第二个和第四个因数趋近 1，第三个因数趋近 \(e^{-\lambda}\)（这是指数函数的定义属性之一）。因此，我们得出

\[\lim_{n \to \infty} \mathbb{P}(X = k) = \frac{\lambda^k}{k!} e^{-\lambda} \]

这表明泊松分布是二项式分布的一种极限情况。

图 2.8 给出了其 pmf 图表的示例


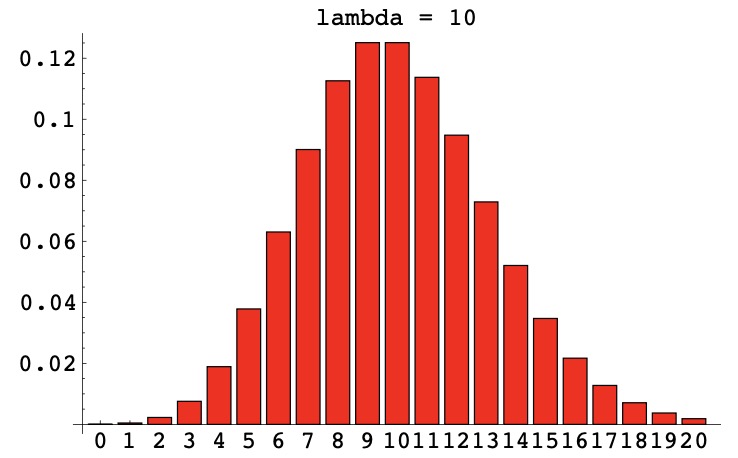
图 2.8 Poi(10)分布的 pdf

我们得出一些属性。
  1. 根据示例2.8 推导出PGF：\(G(z)=e^{-\lambda(1-z)}\)
  2. 由此得出期望为 EX = G′(1) = λ。直观的解释是，对应的抛硬币实验的平均成功次数为 np = n(λ/n) = λ。
  3. 上述论点表明方差应该是 n(λ/n)(1 − λ/n) → λ。事实确实如此，因为

\[Var(X)=G''(1)+G'(1)-(G'(1))^2=\lambda^2+\lambda-\lambda^2=\lambda \]

因此，泊松分布的方差和期望是相同的。

2.5.5 超几何分布(Hypergeometric Distribution)

当随机变量 X 具有参数 N、n 和 r 并且对于\(max\{0,r+n-N\} \leq k \leq min\{n,r\}\)满足

\[\mathbb{P}(X=k)=\frac{\binom{r}{k}\binom{N-r}{n-k}}{\binom{N}{n}} \]

时，我们称 X 具有超几何分布。
我们写作X～Hyp(n,r,N)。超几何分布用于以下场景。

考虑一个有 N 个球的瓮，其中 r 个是红色的。我们从瓮中随机抽取 n 个球，不放回。 n 个选定的球中红球的数量具有 Hyp(n, r, N ) 分布。也就是说，如果我们将红球编号为 1, …, r ，其余球编号为 r+1,...,N ，则随机实验的结果总数为 \(\binom{N}{n}\)，每个结果都有相同可能性。 “k 个球是红球”的事件结果数为 \(\binom{r}{k} \times \binom{N-r}{n-k}\) ，因为 k 个球必须从 r 个红球中抽取，而剩余的 n − k 个球必须抽取从 N − k 个非红球中抽取。我们得到表格：

红 非红 总计
选中 k n - k n
未选中 r - k N - n - r + k N - n
总计 r N - r N

示例 2.9 从一整副 52 张牌中选择五张牌。令 X 为 A 的数量。那么 X ∼ Hyp(n = 5,r = 4,N = 52)。

k 0 1 2 3 4 Σ
P(X = k) 0.659 0.299 0.040 0.002 0.000 1

超几何分布的期望和方差为

\[\mathbb{E}X=n\frac{r}{N} \]

和

\[Var(X)=n\frac{r}{N}(1-\frac{r}{N})\frac{N-n}{N-1} \]

请注意，这与二项式情况的期望和方差非常相似，其中 p = r/N。证明将在第 4 章中给出（参见示例 4.7 和 4.10）。

posted @ 2024-12-31 11:57  李思默  阅读(132)  评论(0)    收藏  举报