《概率入门》 1.3 事件（Events）

通常我们对单一结果不感兴趣，但对结果集中的某一个是否发生感兴趣。这种样本空间的子集被称为事件。事件将用大写字母 A，B，C ，… 表示。如果实验的结果是 A 中的一个，我们就说事件 A 发生。

事件的示例有：

1. 两个骰子之和为 10 或以上的事件，
   A = {(4, 6), (5, 5), (5, 6), (6, 4), (6, 5), (6, 6)}.
2. 机器寿命少于1000天的事件，
   A = [0, 1000).
3. 五十名入选者中有五人是左撇子的事件，
   A = {5}.

示例1.5（抛硬币） 假设一枚硬币被抛3次，我们“记录”每一个正面(head)和反面(tail)（不仅仅是正面或反面的数量）。样本空间可以写为
Ω = {HHH,HHT,HTH,HTT,THH,THT,TTH,TTT}

这里，如 HTH 表示第一次抛掷是正面，第二次是反面，第三次是正面。另一种样本空间是长度为 3 的二进制向量 {0,1}³ 的集合，例如，HTH 对应于 (1,0,1)，THH 对应于 (0,1,1)。
第三次抛掷正面的事件 A 是
A = {HHH,HTH,THH,TTH}

由于事件是集合，我们可以对它们应用通常的集合运算：

1. 集合 A ∪ B（A union B）是A或B或两者都发生的事件，
2. 集合 A ∩ B（A intersection B）是 A 和 B 都发生的事件，
3. 事件 （A^c complement）是 A 不发生的事件，
4. 如果 A⊂B(A is a subset of B)，则事件 A 表示(imply)事件 B。

没有共同结果的两个事件 A 和 B，即 A ∩ B = ∅，称为不相交事件(disjoint events)。

示例 1.6 假设我们连续掷两个骰子。样本空间为 Ω = {(1,1),(1,2),...,(1,6),(2,1),...,(6,6)}。将 A = {(6,1),...,(6,6)} 作为第一个骰子为 6 的事件，并且将 B = {(1,6),...,(1,6) } 作为第二个骰子为 6 的事件。则 A∩B = {(6,1),...,(6,6)}∩{(1,6),...,(6,6) } = {(6, 6)} 是两个抛掷都为6的事件.

这在在维恩图(Venn diagram)中描述事件非常有用，如图 1.8 所示：

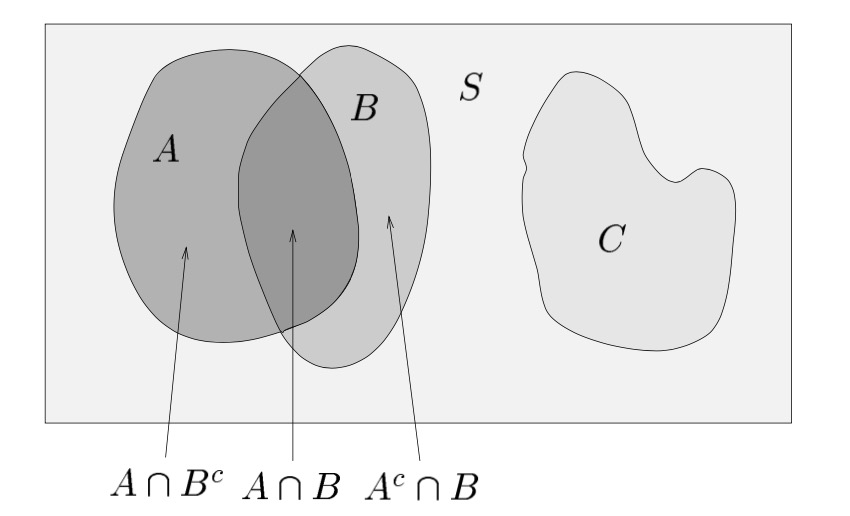
图 1.8 维恩图

在这个维恩图中我们可以看到
(i) A ∩ C = ∅ 因此事件 A 和 C 不相交。

(ii) (A∩B^c)∩(A^c ∩B) = ∅ 因此事件 A∩B^c 和 A^c ∩B 不相交。

示例 1.7（系统可靠性） 图 1.9 描述了三个系统，每个系统由 3 个不可靠的组件组成。串型(series)系统当且仅当所有组件都工作时才工作；并型(parallel)系统当且仅当至少一个组件工作就会工作；2-out-of-3 系统当且仅当 3 个组件中的 2 个可以工作则可以工作。

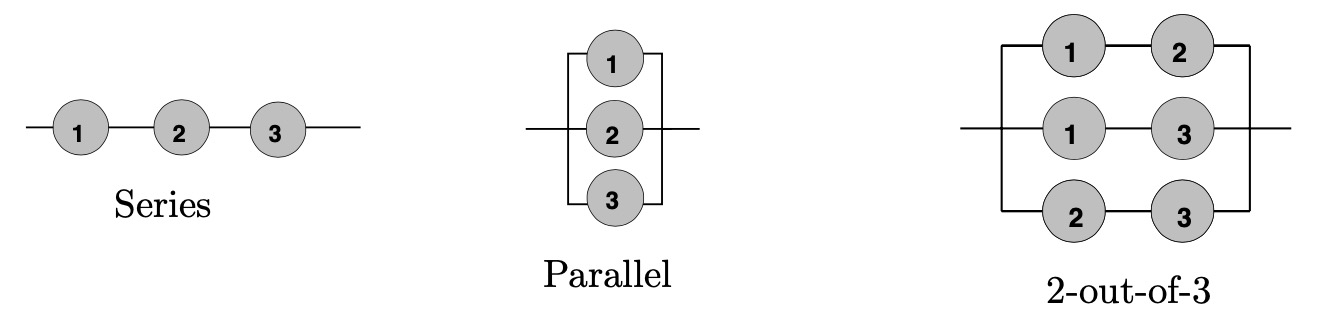
图 1.9 三个不可靠系统

A_i为第 i 个组件工作的事件，i = 1, 2, 3；D_a、D_b、D_c 分别为串型、并型和 2-out-of–3 系统工作的事件。然后，
 D_a = A₁ ∩ A₂ ∩ A₃ ,
然后，
 D_b = A₁ ∪ A₂ ∪ A₃ .
同时
 D_c = (A₁ ∩ A₂ ∩ A₃) ∪ (A₁^c ∩ A₂ ∩ A₃) ∪ (A₁ ∩ A₂^c ∩ A₃) ∪ (A₁ ∩ A₂ ∩ A₃^c)
  = (A₁ ∩ A₂) ∪ (A₁ ∩ A₃) ∪ (A₂ ∩ A₃).

集合(sets)理论中两个有用的结果如下，源自 De Morgan：（摩根定理）

如果 {A_i} 是事件（集合）的集合，那么
\(\left( \bigcup_{i} A_i \right)^c = \bigcap_{i} A_i^c\) （1.1）
并且
\(\left( \bigcap_{i} A_i \right)^c = \bigcup_{i} A_i^c\) （1.2）

这可以通过维恩图轻松证明。请注意，如果我们将 A_i 解释为组件工作的事件，那么 (1.1) 的左侧就是对应并行系统不工作的事件。右侧是所有组件都无法工作的事件。显然这两个事件是相同的。