《概率入门 - 随机实验和概率模型》 1.1 随机实验

由于涉及的公式众多,一些细节翻译可能会有错误,包括原本也存在一些语法上的勘误,希望发现的读者能够指出。
注释:
符号“:=”表示“定义为”
“iid”表示“independent and identically and distributed 独立同分布”
概率的基本概念是随机实验:其结果无法提前确定,但仍需进行分析的实验。
随机实验的例子有:
- 掷骰子,
- 测量布里斯班1月份的降雨量,
- 统计在固定时间段内到达电话交换机的呼叫数量,
- 随机抽取50人,观察左撇子的数量,
- 随机选择十个人并测量他们的身高。
示例 1.1(抛硬币) 最基本的随机实验是抛硬币多次(例如 n 次)。事实上,概率论的大部分内容都可以基于这个简单的实验,正如我们将在后续章节中看到的那样。为了更好地理解这个实验的行为方式,我们可以在数字计算机上进行它,例如在 Matlab 中。下面的简单 Matlab 程序模拟了公平地抛掷 100 次硬币的序列(即正面和反面的可能性相同),并将结果绘制在条形图中。
x = (rand(1,100) < 1/2)
bar(x)
这里 x 是一个包涵 1 和 0 的向量(vector),表示正面和反面。图 1.1 给出了该实验的三个典型结果。
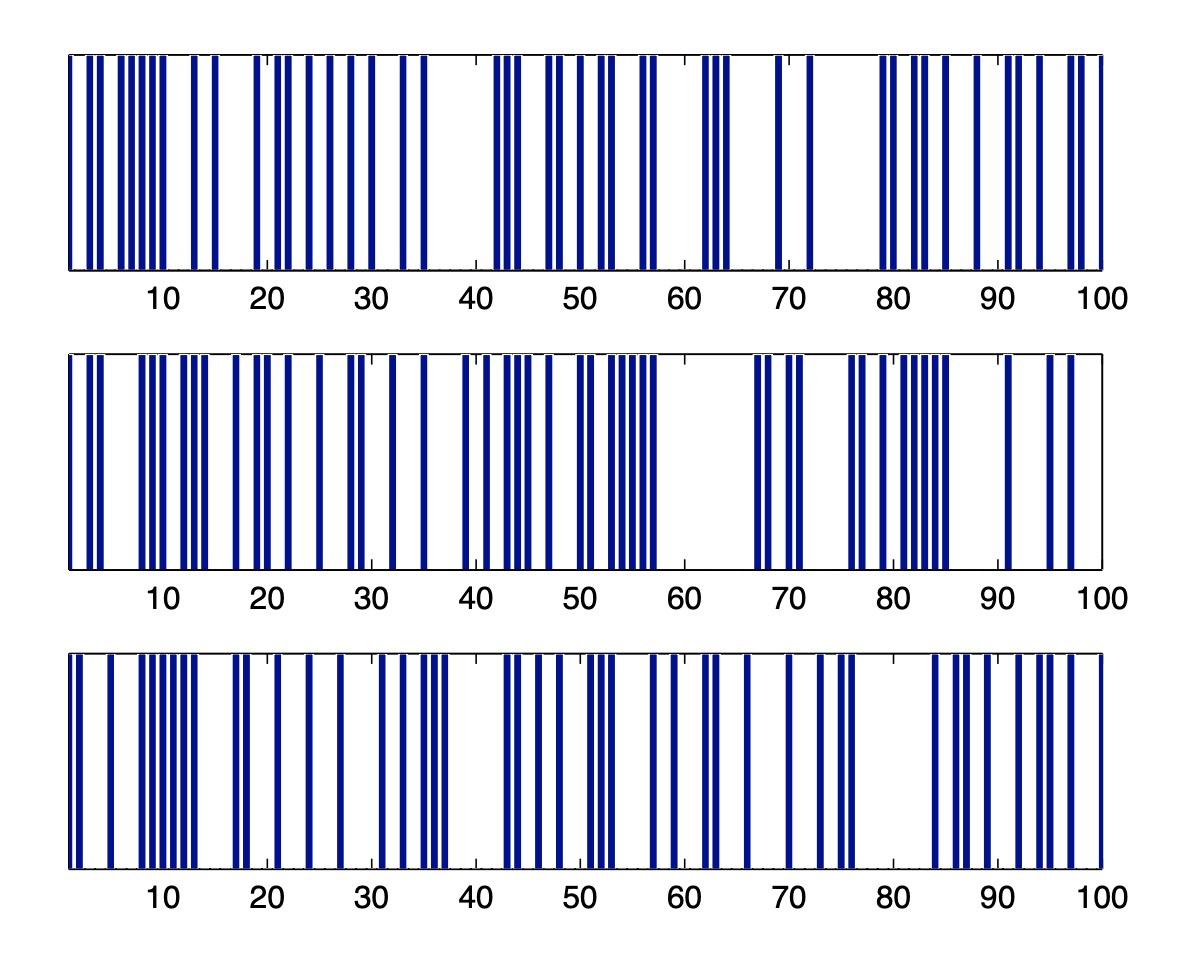
图 1.1:三个实验,每个实验一枚的硬币被抛掷 100 次。黑条表示“正面”(=1) 出现。
y = cumsum(x)./[1:100]
plot(y)
三次实验的结果如图 1.2 所示。请注意,抛出正面的平均次数看起来收敛于 1/2,但存在大量随机波动。
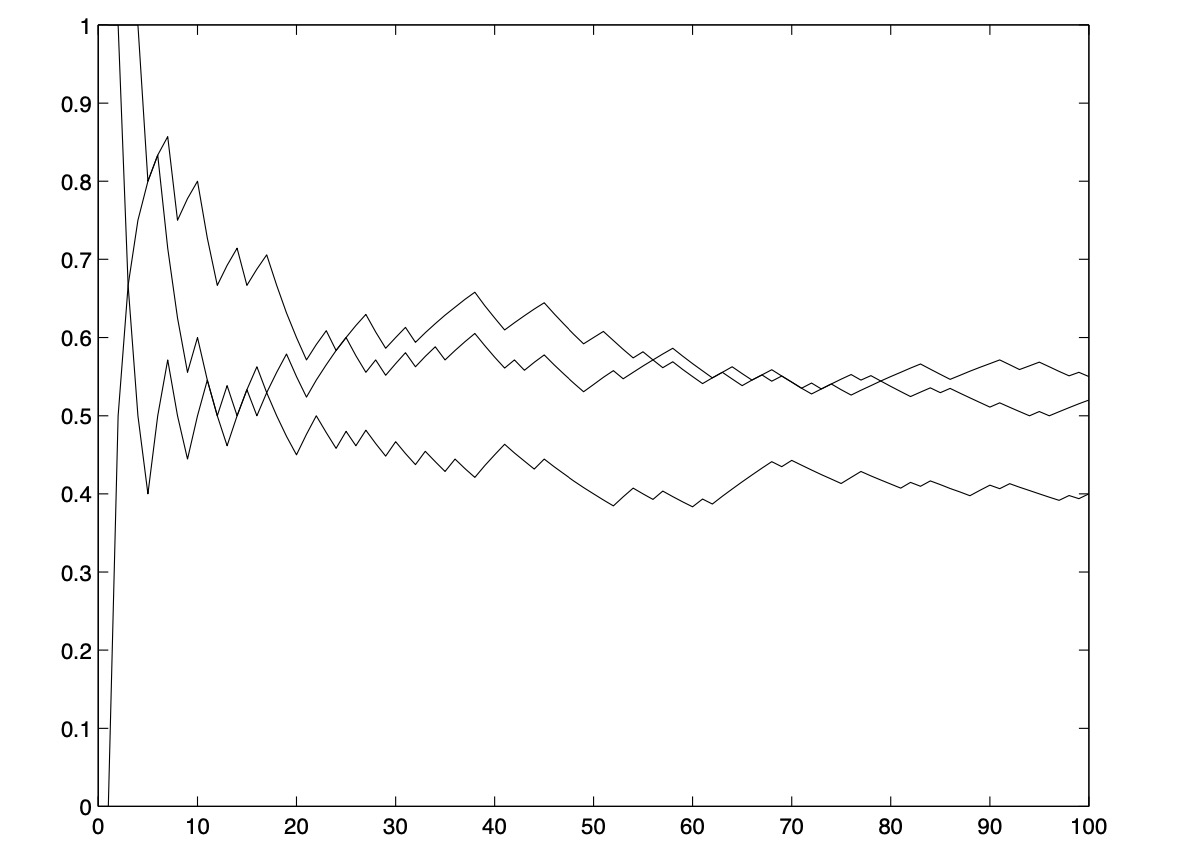
图 1.2:n 次抛掷中抛出正面的平均数量,其中 n = 1,. 。 。 , 100。
示例 1.2(控制图 Control Chart) 控制图(见图 1.3)通常在制造业中作为一种质量控制手段。测量产品的每小时平均产量(例如 10 袋糖的平均重量),以评估产品是否仍然“受控”,例如机器是否平均将正确数量的糖放置在袋子里。当产品 > 控制上限或 < 控制下限时,会发出产品失控的警报,例如,需要调整机器,因为它在袋子中放入的糖过多或不足。问题是如何设置控制范围,因为随机过程自然会围绕其“中心”或“目标”线波动。
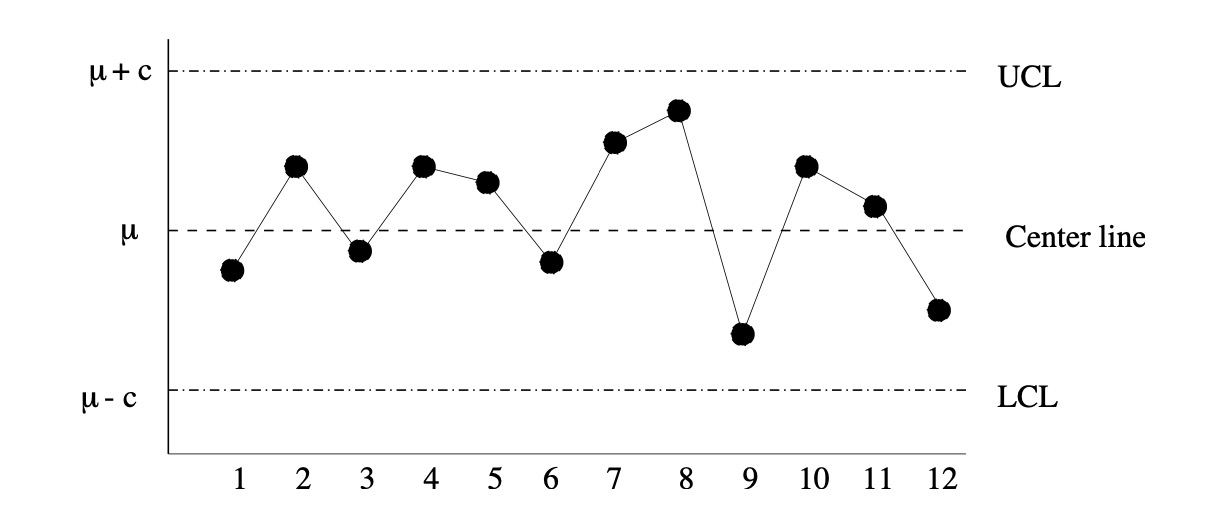
图 1.3 控制图
示例 1.3(机器寿命) 假设对 1000 个相同组件进行长达 50,000 小时的故障监控。这种随机实验的结果通常总结为累积寿命表图,分别如表 1.1 和图 1.3 所示。这里 Fˆ(t) 表示在时间 t 失效的组件的比例。一个问题是如何通过连续函数 F 来建模 Fˆ(t) ,以表示一个典型组件的寿命分布。
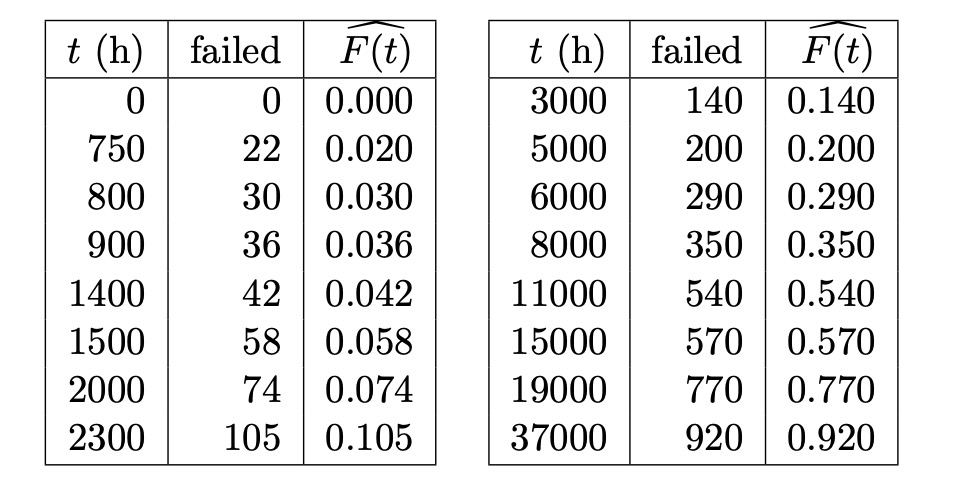
表 1.1 累积寿命表
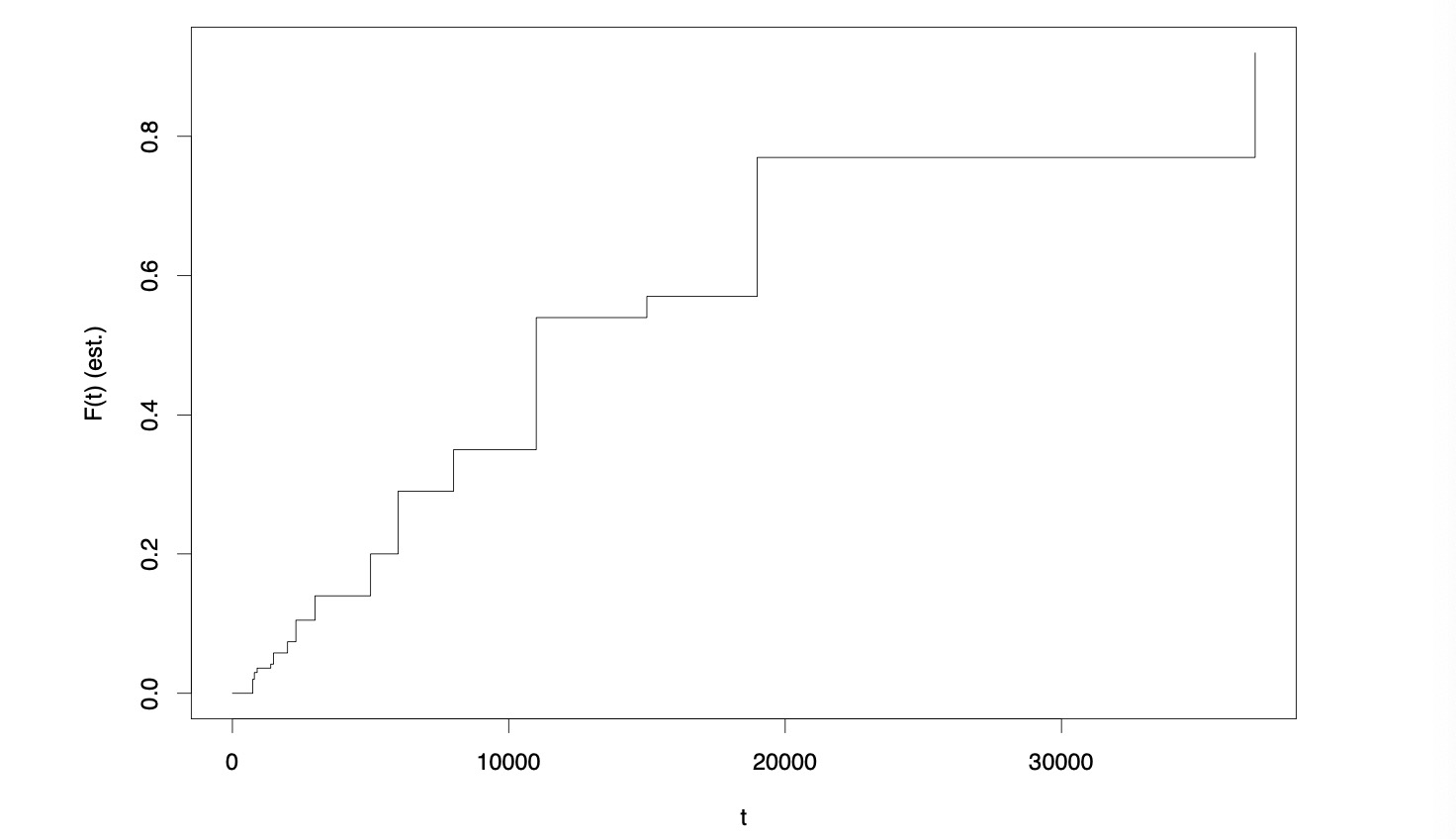
图 1.4 累积寿命表
示例 1.4 一架 4 引擎飞机仅靠每个机翼上的一个引擎就能飞行。所有引擎都不可靠。
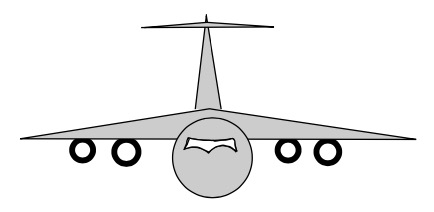
图 1.5:一架有 4 个不可靠引擎的飞机
下面是另外两张随机性的图片。第一个是计算机生成的“植物”,它看起来非常像真正的植物。第二个是真实数据,描述了某些通信链路传输的字节数。一个有趣的特征是,数据可以表现出“分形(fractal)”行为,也就是说,如果将数据统计(aggregated)为更小或更大的时间间隔,就会出现类似的图片。
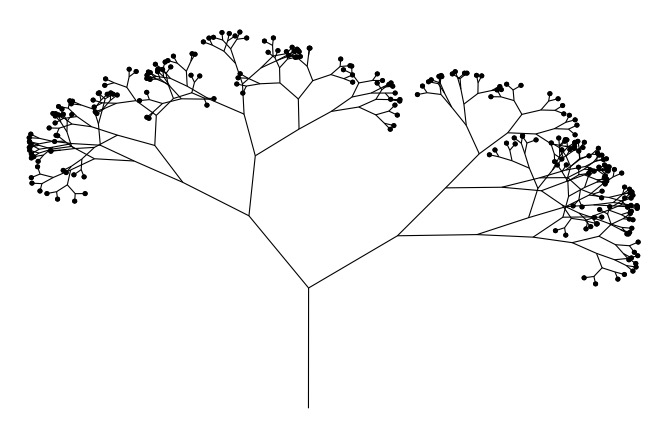
图 1.6 植物生长
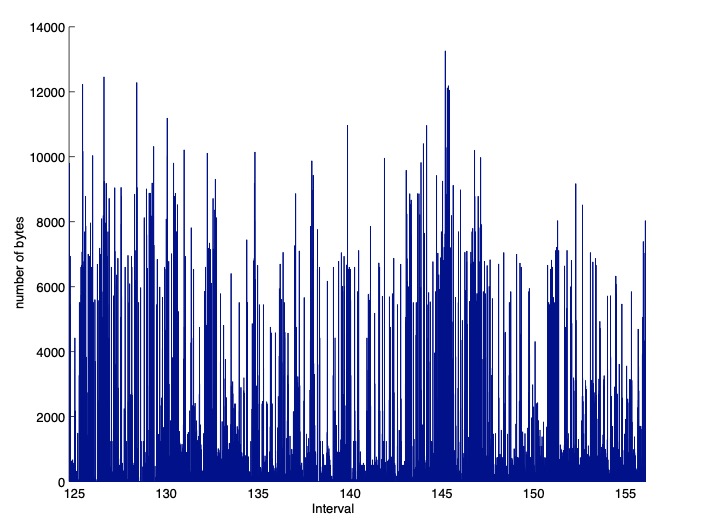
图 1.7 传输数据
我们希望通过适当的数学模型来描述这些实验。这些模型由三个构建块组成:样本空间(sample space)、一组事件(events)和概率(probability)。我们现在将描述每个对象。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号