使用朴素贝叶斯算法简单实现垃圾邮件过滤之算法介绍

一、算法介绍

朴素贝叶斯法，简称NB算法，是贝叶斯决策理论的一部分，是基于贝叶斯定理与特征条件独立假设的分类方法：

首先理解两个概念：

· 先验概率是指根据以往经验和分析得到的概率，它往往作为“由因求果”问题中的“因”出现；

· 后验概率是指在得到“结果”的信息后重新修正的概率，是“执果寻因”问题中的“因” 。

1 贝叶斯定理

贝叶斯理论是以18世纪的一位神学家托马斯贝叶斯(Thomas Bayes)命名。通常，事件A在事件B（发生）的条件下的概率，与事件B在事件A（发生）的条件下的概率是不一样的；然而，这两者是有确定的关系的，贝叶斯定理就是这种关系的陈述。贝叶斯公式：

 

或者可以一般地表示为：

 

 

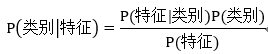
以邮件过滤为例：

·Pr(S)   ：垃圾邮件的概率；

·Pr(H)   ：正常邮件的概率；

·Pr(W|S) ：垃圾邮件中，词汇W的概率；

·Pr(W|H) ：正常邮件中，词汇W的概率；

·Pr(S|W) ：邮件为垃圾邮件(spam)的概率，在已知词汇W的条件下。

 

2 特征条件独立

给定样本的属性之间是相互独立的，比如：以判定邮件是否为垃圾邮件为例，其中判定的方法为根据邮件中出现的词语判定是否为垃圾邮件；给定的一封样本邮件，特征条件独立就是指邮件中不同的词出现的概率相互之间是不受影响的，即一个词的出现不会影响另一个词的出现。（虽然此条件往往不成立，但是NB算法依然取得了较好的分类效果）。

3 基本定义

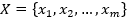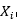首先基于特征条件独立，假设学习输入或输出的联合概率分布；然后基于此模型，对给定的待分类的样本，求解在出现的条件下各个类别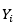出现的概率，哪个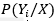的概率最大，就把它归到哪个类别。

·设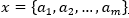为一个待分类项，每个a为x的一个特征属性。

·有类别集合。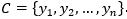

·计算。

·如果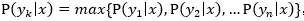，则 。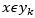

 

计算第3步中的各个条件概率时可以这么做：

·找到一个已知分类的待分类项集合，这个集合叫做训练样本集。

·统计得到在各类别下各个特征属性的条件概率估计。即：

 

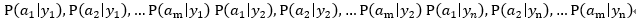
·如果各个特征属性是条件独立的，则根据贝叶斯定理有如下推导：

 

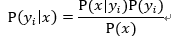
因为分母对于所有类别为常数，因此只要将分子最大化即可。又因为各特征属性是条件独立的，所以有：

 

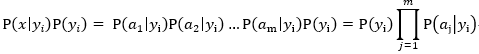
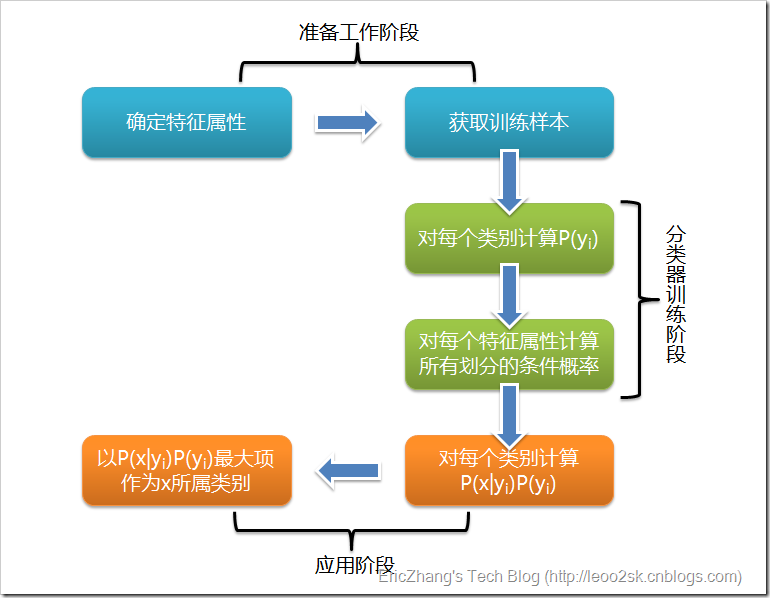
这些过程可用下图概括：

4 优缺点

朴素贝叶斯的主要优点有：

·朴素贝叶斯模型发源于古典数学理论，有稳定的分类效率。

·对小规模的数据表现很好，能个处理多分类任务，适合增量式训练。

·对缺失数据不太敏感，算法比较简单，常用于文本分类。

朴素贝叶斯的主要缺点有：　　　

·理论上朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此。因为朴素贝叶斯模型给定输出类别的情况下，假设属性之间相互独立，这个假设在实际应用中往往是不成立的，在属性个数比较多或者属性之间相关性较大时，分类效果并不好。而在属性相关性较小时，朴素贝叶斯性能最为良好。对于这一点，有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。

·需要知道先验概率，且先验概率很多时候取决于假设，假设的模型可以有很多种，因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。

·由于是通过先验和数据来决定后验的概率从而决定分类，所以分类决策存在一定的错误率。

·对输入数据的表达形式很敏感。