树状数组
树状数组
树状数组,又称二叉索引树(Binary Indexed Tree,BIT)
是一种用来维护序列动态前缀和的数据结构
一、找序列中第k小: P1168 中位数 - 洛谷
先离散化原数组,然后运用到树上倍增找第k小
//离散化
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
b[i]=a[i];//副本
}
sort(a+1,a+1+n);//排序
tot=unique(a+1,a+1+n)-a-1;//去重
for(int i=1;i<=n;i++){
b[i]=lower_bound(a+1,a+1+tot,b[i])-a;//将原来的数按相对大小变为1~n的数
}
因为先输入的数不用和后边比较,所以一边加点一边输出前奇数项的中位数
for(int i=1;i<=n;i++){
add(b[i],1);//动态加点
if(i&1){
int res=select((i+1)>>1);//找第k小
cout<<a[res]<<endl;
}
}
select函数找第k小
int select(const T &k) {
int x = 0;
T cur{};
for (int i = 1 << __lg(n); i; i /= 2) {
if (x + i <= n && cur + a[x + i] < k) {
x += i;
cur = cur + a[x];
}
}
return x+1;
//因为需要找>=k的最小x,就是求<k的最大x +1
}
};
完整代码:
int n,m,q,tot;
int a[N],b[N],c[N];
void add(int x,int v){
for(;x<=n;x+=lowbit(x)) c[x]+=v;
}
int query(int x){
int sum=0;
for(;x;x-=lowbit(x)) sum+=c[x];
return sum;
}
int query(int l,int r){
return query(r)-query(l-1);
}
int select(int k) {
//找前缀和<=k最大的x 前缀和必须单增
//树状数组中a[x]维护的是[x-lowbit(x)+1,x]的区间和
int x=0,cur=0;
for (int i=(1<<__lg(n));i;i>>=1) {
if(x+i<=tot&&cur+c[x+i]<k) {
//a[x+i]为[x+1,x+i]的区间和,i为2的幂
//倍增枚举二进制位扩展
x+=i;
cur=cur+c[x];
}
}
return x+1;
}
void solve(){
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
b[i]=a[i];
}
sort(a+1,a+1+n);
tot=unique(a+1,a+1+n)-a-1;
for(int i=1;i<=n;i++){
b[i]=lower_bound(a+1,a+1+tot,b[i])-a;
// cout<<b[i]<<' ';
}
// cout<<endl;
for(int i=1;i<=n;i++){
add(b[i],1);
if(i&1){
int res=select((i+1)>>1);
cout<<a[res]<<endl;
}
}
}
二、维护前缀和: [P6225 eJOI 2019] 异或橙子 - 洛谷
首先对于一般的维护前缀和问题,求[l,r]区间的前缀和就是query(r)^query(l-1)
有一个最重要点的我们要知道: 树状数组其实就是差分,对于简单的区间改的问题一般都是一阶差分,后面会讲二阶差分问题,如果能明白差分的原理和会推出怎么差分,几阶差分,差分怎么得出原数组,怎么用树状数组维护,那是最好的。
对于本题而言,我们需要求的是总异或和, 即a1⊕a2⊕a3⊕(a1⊕a2)⊕(a2⊕a3)⊕(a1⊕a2⊕a3)
我们发现对于[l,r]区间的总异或和就是a1^a3,2被消完了
再举几个例子:
[1,3] : a1^a3
[1,4] : 相比于[1,3]多异或的a4^(a3^a4)^(a2^a3^a4)^(a1^a2^a3^a4)=a1^a3 即(a1^a3)^(a1^a3)=0
欸?居然是0,而且根据异或的规律,对于一个数x,异或奇数次后是x,异或偶数次后是0
再比如:
[2,4] : 就是a2^a4
根据我们所观察出来的,大胆假设然后去验证就好了,我们发现,当 l 和 r 同是奇数或偶数时,结果就是奇数或偶数的前缀和,因为只有这两种情况时,区间中的下标为偶数或奇数的出现了偶数次,即异或为0,剩下的出现奇数次即为答案
那么对于 l 和 r 一个奇一个偶时,结果就是0
所以对于本题,只需要分别维护下标为奇数和偶数的前缀和,然后根据 l 和 r 的关系求出答案就好了
代码如下:
const int N=2e5+10;
int n,q;
int a[N],odd[N],even[N];
void add(int x,int v){
for(int i=x;i<=n;i+=lowbit(i)){
if(x&1) odd[i]^=v;
else even[i]^=v;
}
}
int query(int x,int v[]){
int sum=0;
for(int i=x;i;i-=lowbit(i)){
sum^=v[i];
}
return sum;
}
int query(int l,int r){
if(l&1) return (query(r,odd)^query(l-1,odd));
return (query(r,even)^query(l-1,even));
}
void solve(){
cin>>n>>q;
for(int i=1;i<=n;i++){
cin>>a[i];
add(i,a[i]);
}
while(q--){
int op,x,y;
cin>>op>>x>>y;
if(op==1){
add(x,y^a[x]);
a[x]=y;
}
if(op==2){
if((x&1)!=(y&1)){
cout<<0<<endl;
continue;
}
cout<<query(x,y)<<endl;
}
}
}
三、差分加上等差数列(二阶差分): P1438 无聊的数列 - 洛谷
对$[l,r]$区间加一个首项为k,公差为d的等差数列,如下表:
| l | l+1 | …… | x | …… | r | r+1 | r+2 | |
|---|---|---|---|---|---|---|---|---|
| 增加 | k | d+k | xd+k | (r-l)d+k | 0 | 0 | ||
| 一阶差分 | k | d | d | d | d | d | -(r-l)d-k | 0 |
| 二阶差分 | k | d-k | 0 | 0 | 0 | 0 | -(r-l+1)d-k | (r-l)k |
观察发现,想要对差分加一个等差数列,只需要令二阶差分的c[l]+=k,c[l+1]+=d-k,c[r+1]+=-(r-l+1)d-k,c[r+2]+=(r-l)d+k
这样就能维护这个前缀和了,
想要查第p个数是多少只需要前缀和两次就可以了,
关于怎么推的参考博客: P1438 无聊的数列 题解(改) - 洛谷专栏
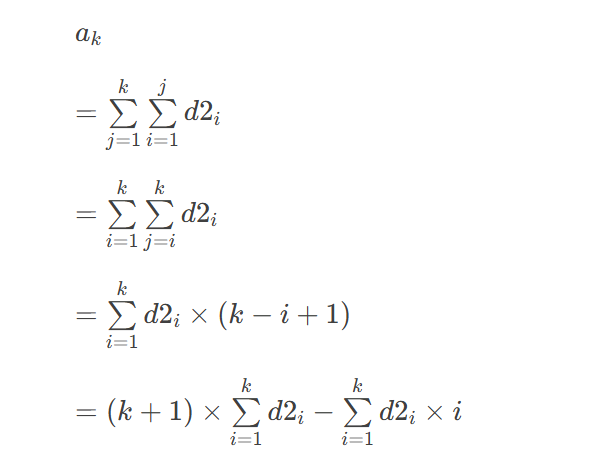
所以我们可以用两个数组分别维护二阶差分c[i]和d[i]=i*c[i],
代码如下:
int n,m;
int a[N],b[N],c[N],d[N];
void add(int x,int v){
for(int i=x;i<=n;i+=lowbit(i)){
c[i]+=v;
d[i]+=x*v;
}
}
int query(int x){
int sum=0;
for(int i=x;i;i-=lowbit(i)){
sum+=(x+1)*c[i]-d[i];
}
return sum;
}
void solve(){
cin>>n>>m;
for(int i=1;i<=n;i++){
cin>>a[i];
b[i]=a[i]-a[i-1];//一阶差分
add(i,b[i]-b[i-1]);//加入二阶差分
}
while(m--){
int op;
cin>>op;
if(op==1){
int l,r,k,d;
cin>>l>>r>>k>>d;
add(l,k);
add(l+1,d-k);
add(r+1,-(r-l+1)*d-k);
add(r+2,k+(r-l)*d);
}else{
int p;
cin>>p;
cout<<query(p)<<endl;
}
}
}
四、离线处理+查询区间中种类数 : [P1972 SDOI2009] HH的项链 - 洛谷
为节省效率,我们用离线处理
先将所有要查询的区间存入并按r的升序排序
同时我们加点的时候需要用pre[]]数组记录a[i]上次出现的位置,如果第一次出现就是0,然后我们需要知道的是,如果区间中出现相同值,那么我们选择将最右边的值记为1,前边的为0,这样按r从小到大扫的时候就可以一直保持区间中出现那个值了,不必再回找了。
最开始的时候设一个起点begin=1,然后到每个r扫过去并记录答案就好了
还有一点就是,我们c[i]数组记录的是a[i]是否出现,出现+1,不出现为0,多出现只需要将上个位置-=,这个位置+1
完整代码:
#include <bits/stdc++.h>
using namespace std;
//-------------------------------------------------------------------------------------------
#define int long long
#define R ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define P pair<int,int>
#define lowbit(x) (x&(-x))
#define dbg1(x) cout<<"# "<<x<<endl
#define dbg2(x,y) cout<<"# "<<x<<" "<<y<<endl
#define endl '\n'
const int mod=998244353;
const int N=1e6+10;
const int INF=0x3f3f3f3f3f3f3f3f;
const int inf=0x3f3f3f3f;
//--------------------------------------------------------------------------------------
int n,q;
int a[N],c[N],pre[N],ans[N];
struct info{
int l,r,id;
friend bool operator < (info a,info b){
return a.r<b.r;
}
}res[N];
inline int read(){
int x=0;char c=getchar();
while (c<'0'||c>'9') c=getchar();
while (c>='0'&&c<='9') x=(x<<1)+(x<<3)+c-48,c=getchar();
return x;
}
inline void write(int x){
if (x>=10) write(x/10);
putchar(x%10+48);
}//快读快输
void add(int x,int v){
for(;x<N;x+=lowbit(x)) c[x]+=v;
}
int query(int x){
int sum=0;
for(;x;x-=lowbit(x)) sum+=c[x];
return sum;
}
int query(int l,int r){
return query(r)-query(l-1);
}
void solve(){
n=read();
for(int i=1;i<=n;i++){
a[i]=read();
}
q=read();
for(int i=1;i<=q;i++){
res[i].id=i;
res[i].l=read();
res[i].r=read();
}
sort(res+1,res+1+q);//排序
int beg=1;//起点
for(int i=1;i<=q;i++){
for(int j=beg;j<=res[i].r;j++){
add(j,1);
if(pre[a[j]]) add(pre[a[j]],-1);//如果出现过,将上个位置-1
pre[a[j]]=j;
}
ans[res[i].id]=query(res[i].l,res[i].r);
beg=res[i].r+1;
}
for(int i=1;i<=q;i++){
cout<<ans[i]<<endl;
}
}
signed main(){
R;
// freopen("jia.in","r",stdin);
// freopen("jia.out","w",stdout);
int T=1;
//cin>>T;
for(int i=1;i<=T;i++){
solve();
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号