IDEA加密算法原理

一、简述

IDEA的全称是International Data Encryption Algorithm，也叫做国际加密算法

这种算法是在DES算法的基础上发展出来的，类似于三重DES

数据块加密算法

二、加密步骤

1、产生密钥

2、加解密过程

 

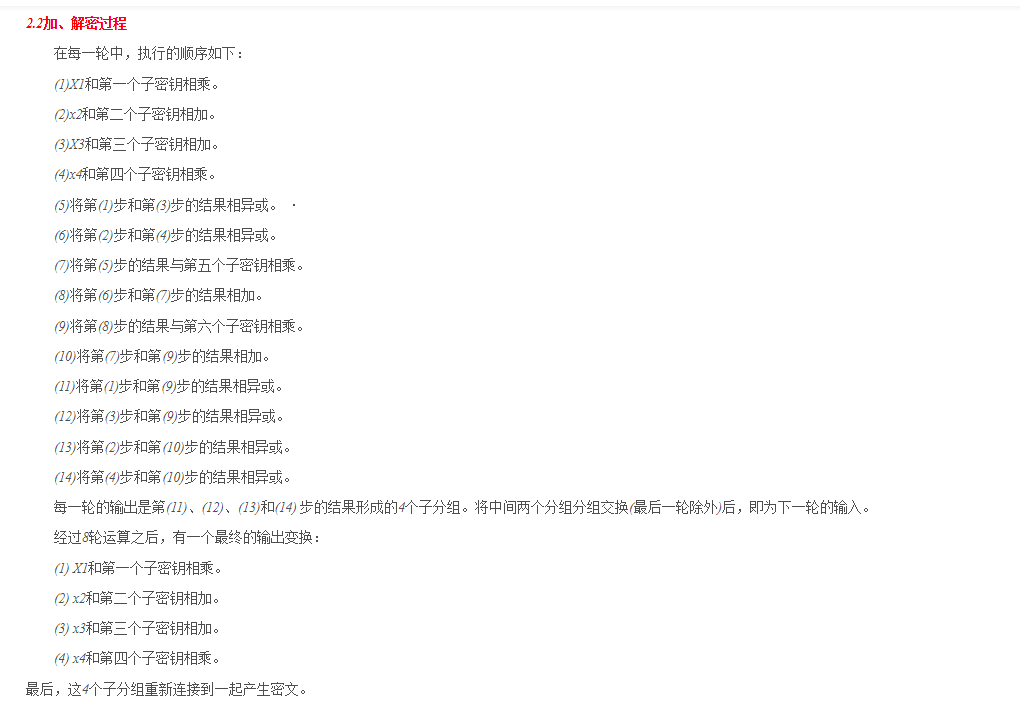
三、代码实现(抄的网上的代码)

#include<iostream>
#include<bitset>
#include<math.h>
using namespace std;
typedef bitset<16> code; //16位
typedef bitset<128> key; //128位秘钥
 
bitset<16> sub_key[52];  //52个子秘钥
bitset<16> inv_sub_key[52];//52个逆子秘钥
bitset<64> plaint_txt;
 
//异或运算
code XOR(code code_1, code code_2)
{
    return code_1 ^ code_2;
}
 
//加法运算
code Plus(code code_1, code code_2)
{
    int tmp = 0;
    code result;
    for (int i = 0; i < 16; i++) //二进制转换成十进制
    {
        tmp += code_1[i] * pow(2, i) + code_2[i] * pow(2, i);
    }
    tmp %= 65536;
    bitset<16>binary(tmp); //转换成二进制
    for (int i = 0; i < 16; i++)
        result[i] = binary[i];
 
    return result;
}
 
//逆加法
code invPlus(code code_in)
{
    int tmp = 0;
    code result;
    for (int i = 0; i < 16; i++) //二进制转换成十进制
        tmp += code_in[i] * pow(2, i);
    tmp = 65536 - tmp;
    bitset<16>binary(tmp); //转换成二进制
    for (int i = 0; i < 16; i++)
        result[i] = binary[i];
 
    return result;
 
}
//乘法运算
code Times(code code_1, code code_2)
{
    code result;
    long long tmp;
    long long tmp_1 = 0, tmp_2 = 0;
    for (int i = 0; i < 16; i++)  //二进制转换成十进制
    {
        tmp_1 += code_1[i] * pow(2, i);
        tmp_2 += code_2[i] * pow(2, i);
    }
    if (code_1 == 0)
        tmp_1 = 65536;
    if (code_2 == 0)
        tmp_2 = 65536;
 
    tmp = (tmp_1 * tmp_2) % 65537;
    if (tmp == 65536)  //如果得到最大值即等价于0x0000
        result = 0x0000;
    else
    {
        bitset<16>binary(tmp); //转换成二进制
        for (int i = 0; i < 16; i++)
            result[i] = binary[i];
    }
    return result;
}
 
void Exgcd(int a, int b, int& x, int& y) //欧几里得扩展算法
{
    if (!b)
        x = 1, y = 0;
    else
        Exgcd(b, a % b, y, x), y -= a / b * x;
}
//利用欧几里得扩展算法求乘法的逆
code invTimes(code code_in)
{
    code result;
    int tmp = 0;
    for (int i = 0; i < 16; i++)  //首先转换成十进制
        tmp += code_in[i] * pow(2, i);
 
    int x, y;
    int p = 65537;
    Exgcd(tmp, p, x, y);
    x = (x % p + p) % p;  //x即为tmp在 (mod65537) 的乘法逆
    bitset<16>binary(x); //转换成二进制
    for (int j = 0; j < 16; j++)
        result[j] = binary[j];
 
    return result;
}
//子秘钥生成
void subkeys_get(code keys_input[8])//输入8个16bit组
{
    key keys;
    for (int i = 0; i < 8; i++)  //转化成128位
    {
        for (int j = 0; j < 16; j++)
        {
            keys[j + 16 * i] = keys_input[7 - i][j];
        }
    }
    for (int i = 0; i < 8; i++)  //前8个子秘钥（不移动）
    {
        for (int j = 0; j < 16; j++)
            sub_key[i][15 - j] = keys[127 - (j + 16 * i)];
    }
    for (int i = 0; i < 5; i++)  //中间40个子秘钥（）每次循环左移25位
    {
        key tmp_keys = keys >> 103;
        keys = (keys << 25) | (tmp_keys);
        for (int j = (8 + 8 * i); j < (8 * (i + 2)); j++)
        {
            for (int k = 0; k < 16; k++)
                sub_key[j][15 - k] = keys[127 - (k + 16 * (j - 8 - 8 * i))];
        }
    }
    key tmp_keys = keys >> 103;   //最后一次循环左移取前四个
    keys = (keys << 25) | (tmp_keys);
    for (int i = 48; i < 52; i++)
    {
        for (int j = 0; j < 16; j++)
            sub_key[i][15 - j] = keys[127 - (j + 16 * (i - 48))];
    }
}
void inv_subkeys_get(code sub_key[52])  //将52个子秘钥调用
{
    //生成逆子秘钥
    for (int i = 6; i < 48; i = i + 6)   //U_1, U_2, U_3, U_4   (2 <= i <= 8)
    {
        inv_sub_key[i] = invTimes(sub_key[48 - i]);
        inv_sub_key[i + 1] = invPlus(sub_key[50 - i]);
        inv_sub_key[i + 2] = invPlus(sub_key[49 - i]);
        inv_sub_key[i + 3] = invTimes(sub_key[51 - i]);
    }
    for (int i = 0; i < 48; i = i + 6)    //U_5, U_6   (1 <= i <= 8)
    {
        inv_sub_key[i + 4] = sub_key[46 - i];
        inv_sub_key[i + 5] = sub_key[47 - i];
    }
    //U_1, U_2, U_3, U_4   (i = 1, 9)
    inv_sub_key[0] = invTimes(sub_key[48]);
    inv_sub_key[1] = invPlus(sub_key[49]);
    inv_sub_key[2] = invPlus(sub_key[50]);
    inv_sub_key[3] = invTimes(sub_key[51]);
 
    inv_sub_key[48] = invTimes(sub_key[0]);
    inv_sub_key[49] = invPlus(sub_key[1]);
    inv_sub_key[50] = invPlus(sub_key[2]);
    inv_sub_key[51] = invTimes(sub_key[3]);
 
}
//加密
bitset<64> encrypt(bitset<64> plaint)
{
    bitset<16> I_1, I_2, I_3, I_4;
    bitset<64> cipher;
    for (int i = 0; i < 16; i++) //明文分成4个16位(I_1, I_2, I_3, I_4)
    {
        I_1[15 - i] = plaint[63 - i];
        I_2[15 - i] = plaint[47 - i];
        I_3[15 - i] = plaint[31 - i];
        I_4[15 - i] = plaint[15 - i];
    }
    for (int i = 0; i < 48; i = i + 6)  //轮结构运算
    {
        bitset<16> tmp_1 = Times(sub_key[i], I_1);
        bitset<16> tmp_2 = Plus(sub_key[i + 1], I_2);
        bitset<16> tmp_3 = Plus(sub_key[i + 2], I_3);
        bitset<16> tmp_4 = Times(sub_key[i + 3], I_4);
        bitset<16> tmp_5 = XOR(tmp_1, tmp_3);
        bitset<16> tmp_6 = XOR(tmp_2, tmp_4);
        bitset<16> tmp_7 = Times(sub_key[i + 4], tmp_5);
        bitset<16> tmp_8 = Plus(tmp_6, tmp_7);
        bitset<16> tmp_9 = Times(tmp_8, sub_key[i + 5]);
        bitset<16> tmp_10 = Plus(tmp_7, tmp_9);
        I_1 = XOR(tmp_1, tmp_9);
        I_2 = XOR(tmp_3, tmp_9);
        I_3 = XOR(tmp_2, tmp_10);
        I_4 = XOR(tmp_4, tmp_10);
    }
    //输出变换
    bitset<16> Y_1 = Times(I_1, sub_key[48]);
    bitset<16> Y_2 = Plus(I_3, sub_key[49]);
    bitset<16> Y_3 = Plus(I_2, sub_key[50]);
    bitset<16> Y_4 = Times(I_4, sub_key[51]);
 
    for (int i = 0; i < 16; i++) //整合4个输出成密文
    {
        cipher[i] = Y_4[i];
        cipher[i + 16] = Y_3[i];
        cipher[i + 32] = Y_2[i];
        cipher[i + 48] = Y_1[i];
    }
    return cipher;
}
//解密（过程与加密一致，子秘钥变成逆子秘钥）
bitset<64> dencrypt(bitset<64> cipher)
{
 
    //解密
    bitset<16> I_1, I_2, I_3, I_4;
    bitset<64> plaint;
    for (int i = 0; i < 16; i++)
    {
        I_1[15 - i] = cipher[63 - i];
        I_2[15 - i] = cipher[47 - i];
        I_3[15 - i] = cipher[31 - i];
        I_4[i] = cipher[i];
    }
    for (int i = 0; i < 48; i = i + 6)
    {
        bitset<16> tmp_1 = Times(inv_sub_key[i], I_1);
        bitset<16> tmp_2 = Plus(inv_sub_key[i + 1], I_2);
        bitset<16> tmp_3 = Plus(inv_sub_key[i + 2], I_3);
        bitset<16> tmp_4 = Times(inv_sub_key[i + 3], I_4);
        bitset<16> tmp_5 = XOR(tmp_1, tmp_3);
        bitset<16> tmp_6 = XOR(tmp_2, tmp_4);
        bitset<16> tmp_7 = Times(inv_sub_key[i + 4], tmp_5);
        bitset<16> tmp_8 = Plus(tmp_6, tmp_7);
        bitset<16> tmp_9 = Times(tmp_8, inv_sub_key[i + 5]);
        bitset<16> tmp_10 = Plus(tmp_7, tmp_9);
        I_1 = XOR(tmp_1, tmp_9);
        I_2 = XOR(tmp_3, tmp_9);
        I_3 = XOR(tmp_2, tmp_10);
        I_4 = XOR(tmp_4, tmp_10);
    }
    bitset<16> Y_1 = Times(I_1, inv_sub_key[48]);
    bitset<16> Y_2 = Plus(I_3, inv_sub_key[49]);
    bitset<16> Y_3 = Plus(I_2, inv_sub_key[50]);
    bitset<16> Y_4 = Times(I_4, inv_sub_key[51]);
 
    for (int i = 0; i < 16; i++)
    {
        plaint[i] = Y_4[i];
        plaint[i + 16] = Y_3[i];
        plaint[i + 32] = Y_2[i];
        plaint[i + 48] = Y_1[i];
    }
    return  plaint;
 
}
int main()
{
    plaint_txt = 0xa6224adf2f28df73;//64位明文
    //plaint_txt = 0xa795 8723 1f2c 6d73 ;
    cout << "明文：" << endl << plaint_txt << endl;
    code keys_input[8] = { 0x151a, 0x048b, 0x71a1, 0xf9c7, 0x5266, 0xbfd6, 0x24a2, 0xdff1 };//128位秘钥
    
    subkeys_get(keys_input); //生成子秘钥
    inv_subkeys_get(sub_key);//生成逆子秘钥
 
    bitset<64> cipher = encrypt(plaint_txt); //加密得到密文cipher
    cout << "加密得到的密文为：" << endl << cipher << endl;
 
    bitset<64> plaint = dencrypt(cipher);   //解密得到明文plaint
    cout << "解密得到：" << endl << plaint << endl;
 
    return 0;
}

四、特征

1、% 65537 或 % 0x10001

2、有顺序的相乘、相加、相加、相乘操作