图论三种做法:朴素版Dijkstra、堆优化(优先队列)Dijkstra、spfa(队列优化版Bellman-Ford)
【模板】单源最短路径
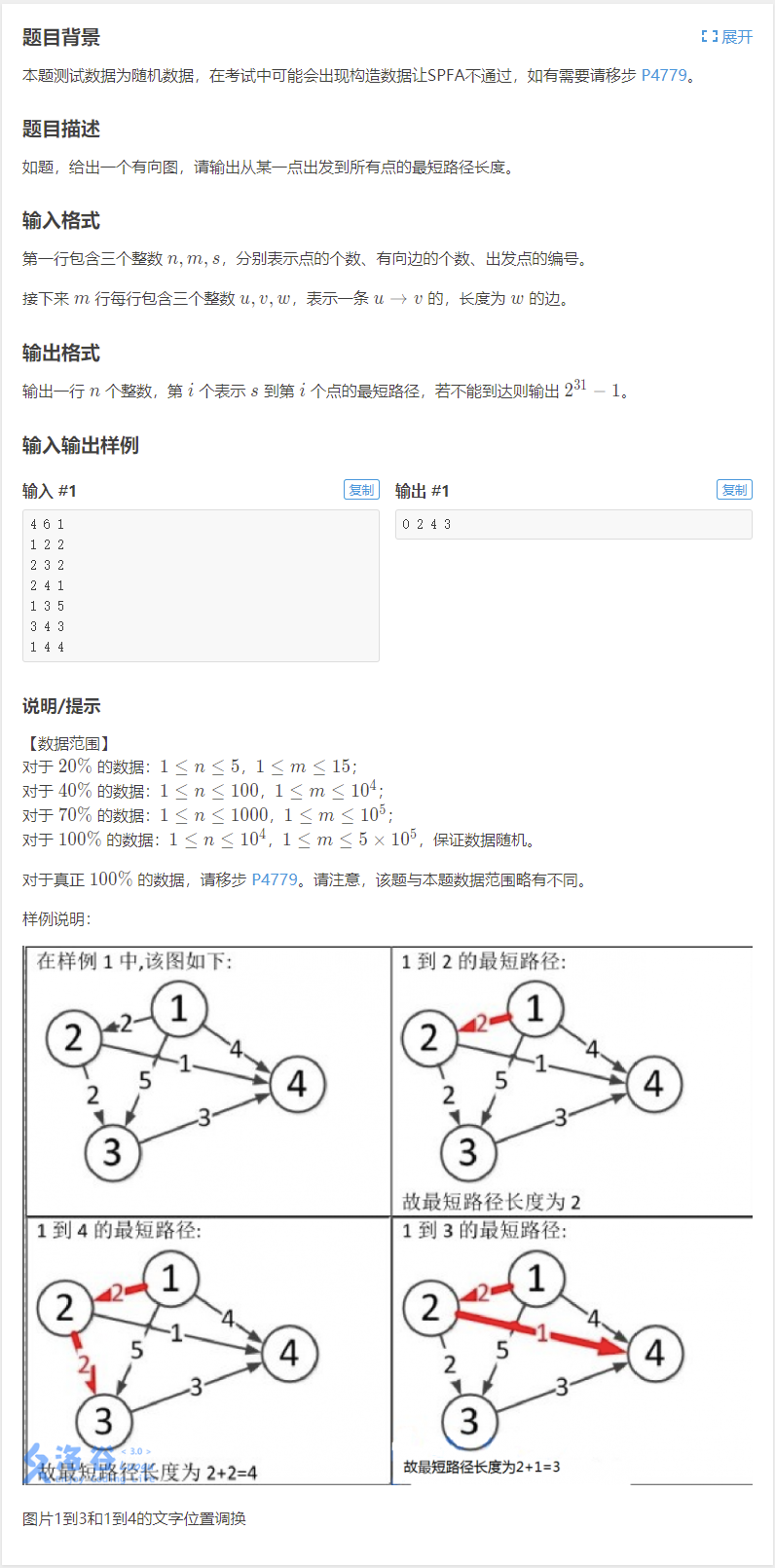
题目传送门:P3371 【模板】单源最短路径(弱)
//1、朴素版Dijkstra #include <iostream> #include <cstring> using namespace std; const int N = 2001, INF = 0x3f3f3f3f; int n, m, S, dist[N], d[N][N]; bool st[N]; void dijkstra() { memset(dist, 0x3f, sizeof dist); dist[S] = 0; for(int i = 0; i < n; i ++) { int t = -1; for(int j = 1; j <= n; j ++) if(!st[j] && (t == -1 || dist[t] > dist[j])) t = j; st[t] = true; for(int j = 1; j <= n; j ++) if(dist[j] > dist[t] + d[t][j]) dist[j] = dist[t] + d[t][j]; } } int main() { cin >> n >> m >> S; memset(d, 0x3f, sizeof d);//注意两点之间的值也要初始化,不然得到的结果全部为0 while(m --) { int a, b, c; cin >> a >> b >> c; d[a][b] = min(d[a][b], c); } dijkstra(); for(int i = 1; i <= n; i ++) { if(dist[i] == 0x3f3f3f3f) cout << 2147483647 << ' '; // 2147483647 = (1 << 31) - 1; else cout << dist[i] << ' '; } cout << endl; return 0; } //2、堆优化版Dijkstra(优先队列) #include <iostream> #include <cstring> #include <queue> using namespace std; const int N = 10001, M = 5e5 + 10, INF = 0x3f3f3f3f; typedef pair<int, int> PII; int n, m, S, d[N], e[M], ne[M], h[N], w[M], idx; bool st[N]; void add(int a, int b, int c) { e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++; } void dijkstra() { memset(d, 0x3f, sizeof d); d[S] = 0; priority_queue<PII, vector<PII>, greater<PII> > q; q.push({0, S}); while(q.size()) { PII t = q.top(); q.pop(); int ver = t.second, distance = t.first; if(st[ver]) continue; st[ver] = true; for(int i = h[ver]; ~i; i = ne[i]) { int j = e[i]; if(d[j] > distance + w[i]) { d[j] = distance + w[i]; if(!st[j]) { q.push({d[j], j}); } } } } } int main() { cin >> n >> m >> S; memset(h, -1, sizeof h); while(m --) { int a, b, c; cin >> a >> b >> c; add(a, b, c); } dijkstra(); for(int i = 1; i <= n; i ++) { if(d[i] == 0x3f3f3f3f) cout << 2147483647 << ' '; else cout << d[i] << ' '; } cout << endl; return 0; } //3、spfa:队列优化版bellman-ford #include <iostream> #include <cstring> #include <queue> using namespace std; const int N = 10001, M = 5e5 + 10, INF = 0x3f3f3f3f; int n, m, S, d[N], e[M], ne[M], h[N], w[M], idx; bool st[N]; void add(int a, int b, int c) { e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++; } void spfa() { memset(d, INF, sizeof d); d[S] = 0; queue<int> q; q.push(S); st[S] = true; while(q.size()) { int t = q.front(); q.pop(); st[t] = false; //spfa可以入队多次,所以入队设为true,出队设为false for(int i = h[t]; ~i; i = ne[i]) { int j = e[i]; if(d[j] > d[t] + w[i]) //注意不要用d[j] = min(d[j], d[t] + w[i]),会超时,if判断比min、max操作快。 { d[j] = d[t] + w[i]; if(!st[j]) { q.push(j); st[j] = true; } } } } } int main() { cin >> n >> m >> S; memset(h, -1,sizeof h); while(m --) { int a, b, c; cin >> a >> b >> c; add(a, b, c); } spfa(); for(int i = 1; i <= n; i ++) { if(d[i] == 0x3f3f3f3f) cout << 2147483647 << ' '; else cout << d[i] << ' '; } cout << endl; return 0; }
注意有些题目可能会卡spfa,因为时间复杂度是O(k * m),最坏情况下会变为O(n * m)。
所以最保险的做法还是堆优化(优先队列)的dijkstra
以下代码可以同时AC P3371 【模板】单源最短路径(弱化版)和 P4779 【模板】单源最短路径(标准版)
//堆优化dijkstra #include <iostream> #include <cstring> #include <queue> using namespace std; typedef pair<int, int> PII; const int N = 1e5 + 10, M = 5e5 + 10, INF = 0x3f3f3f3f; int n, m, S, e[M], ne[M], h[N], w[M], idx, d[N]; bool st[N]; void add(int a, int b, int c) { e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx ++; } void dijkstra() { memset(d, 0x3f, sizeof d); priority_queue<PII, vector<PII>, greater<PII> > q; d[S] = 0; q.push({0, S}); while(q.size()) { PII t = q.top(); q.pop(); int ver = t.second, distance = t.first; if(st[ver]) continue; //dijstra每个点只走一次,所出队后设为true,不再走了 st[ver] = true; for(int i = h[ver]; ~i; i = ne[i]) { int j = e[i]; if(d[j] > distance + w[i]) { d[j] = distance + w[i]; if(!st[j]) //走到的j点是不是没有走过 { q.push({d[j], j}); } } } } } int main() { cin >> n >> m >> S; memset(h, -1, sizeof h); while(m --) { int a, b, c; cin >> a >> b >> c; add(a, b, c); } dijkstra(); for(int i = 1; i <= n; i ++) { if(d[i] == 0x3f3f3f3f) cout << 2147483647 << ' '; else cout << d[i] << ' '; } }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号