【CodeForces训练记录】Codeforces Round 1017 (Div. 4)
训练情况
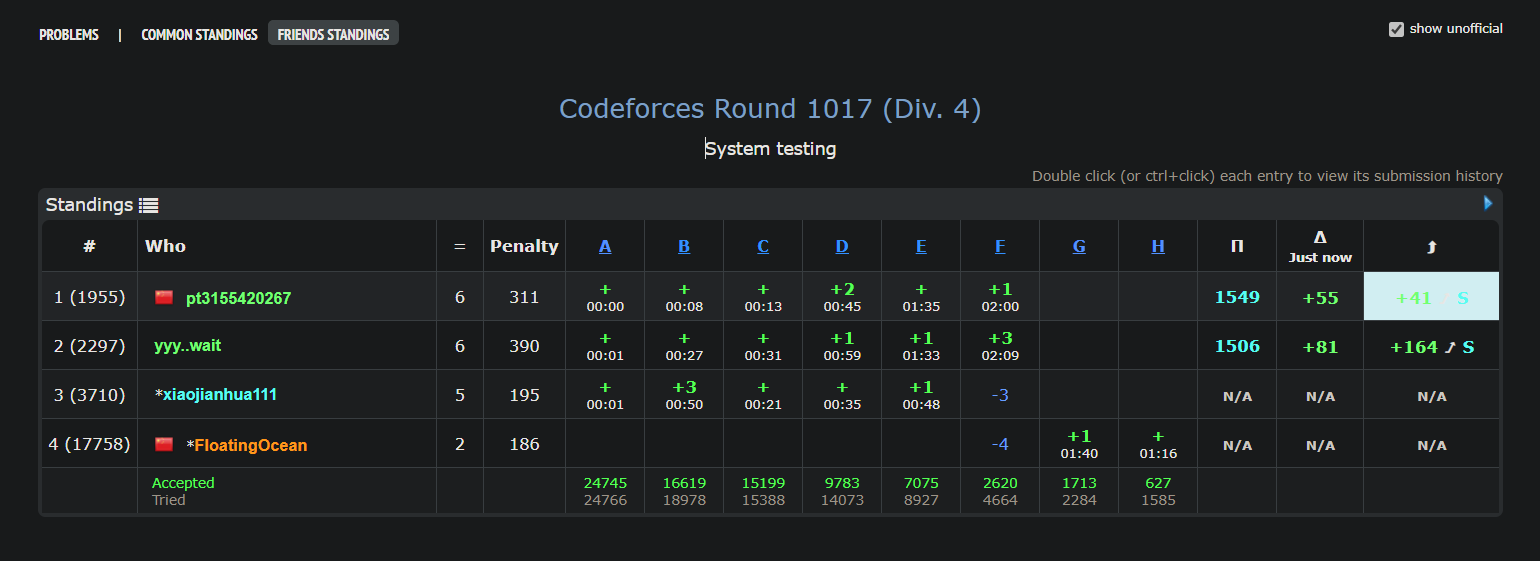
赛后反思
模拟题感觉最近总是写不好,复杂代码实现不大行,感觉D题写成一坨了,但是一坨还是调出来了,F题狗运构造出来了
A题
输出三个字符串的首字母
点击查看代码
#include <bits/stdc++.h>
// #define int long long
#define endl '\n'
using namespace std;
void solve(){
string a,b,c; cin>>a>>b>>c;
cout<<a[0]<<b[0]<<c[0]<<endl;
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int T; cin>>T; while(T--)
solve();
return 0;
}
B题
显然对于任意一种情况都可以,只要保证 \([l,r]\) 覆盖到 \(0\),前后线段长度差刚好为 \(n-m\) 即可,所以我们考虑移动左边界,如果超过 \(0\) 再手动修正一下即可
点击查看代码
#include <bits/stdc++.h>
// #define int long long
#define endl '\n'
using namespace std;
void solve(){
int n,m,l,r; cin>>n>>m>>l>>r;
int ll = l + (n-m);
int rr = r;
if(ll > 0) rr -= ll,ll = 0;
cout<<ll<<" "<<rr<<endl;
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int T; cin>>T; while(T--)
solve();
return 0;
}
C题
二维数组的 \(i+j\) 位是 \(a_{i,j}\),直接开一个数组存起来即可,对于 \(i=1\) 不会更新,因为 \(i+j\) 至少是 \(2\),所以我们根据后面填的数直接判断排列的第一个是什么
点击查看代码
#include <bits/stdc++.h>
// #define int long long
#define endl '\n'
using namespace std;
void solve(){
int n; cin>>n;
vector<vector<int>> a(n + 1,vector<int>(n + 1));
vector<int> ans(2*n + 1),v(2*n+1);
for(int i = 1;i<=n;i++){
for(int j = 1;j<=n;j++){
cin>>a[i][j];
ans[i+j] = a[i][j];
}
}
for(int i = 2;i<=2*n;i++) v[ans[i]]++;
for(int i = 1;i<=2*n;i++){
if(!v[i]){
ans[1] = i;
break;
}
}
for(int i = 1;i<=2*n;i++) cout<<ans[i]<<" "; cout<<endl;
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int T; cin>>T; while(T--)
solve();
return 0;
}
D题
这题怒码 67 行,感觉写的不是很好,开了两个队列储存连续的 \(L\) 和 \(R\),合法的条件首先是两个队列长度要相等,其次是连续的个数,上面的不能超过下面的,或者下面的个数超过上面的两倍,这两个情况判一下不合法即可
点击查看代码
#include <bits/stdc++.h>
// #define int long long
#define endl '\n'
using namespace std;
void solve(){
string s,t; cin>>s>>t;
s+='#'; t+='#';
queue<pair<char,int>> q1;
queue<pair<char,int>> q2;
int cnt[2];
cnt[0] = (s[0] == 'L');
cnt[1] = (s[0] == 'R');
for(int i = 1;i<s.size();i++){
if(s[i] != s[i-1]){
if(s[i-1] == 'L') q1.push({'L',cnt[0]});
else if(s[i-1] == 'R') q1.push({'R',cnt[1]});
cnt[0] = (s[i] == 'L');
cnt[1] = (s[i] == 'R');
} else {
if(s[i] == 'L') cnt[0]++;
else if(s[i] == 'R') cnt[1]++;
}
}
cnt[0] = (t[0] == 'L');
cnt[1] = (t[0] == 'R');
for(int i = 1;i<t.size();i++){
if(t[i] != t[i-1]){
if(t[i-1] == 'L') q2.push({'L',cnt[0]});
else if(t[i-1] == 'R') q2.push({'R',cnt[1]});
cnt[0] = (t[i] == 'L');
cnt[1] = (t[i] == 'R');
} else {
if(t[i] == 'L') cnt[0]++;
else if(t[i] == 'R') cnt[1]++;
}
}
bool flag = true;
if(q2.size() != q1.size()){
cout<<"NO"<<endl;
return;
}
while(q1.size()){
if(q1.front().first != q2.front().first){
flag = false;
break;
}
// cout<<q1.front().second<<" "<<q2.front().second<<endl;
if(2*q1.front().second < q2.front().second || q1.front().second > q2.front().second){
flag = false;
break;
}
q1.pop(); q2.pop();
}
if(flag) cout<<"YES"<<endl;
else cout<<"NO"<<endl;
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int T; cin>>T; while(T--)
solve();
return 0;
}
E题
考虑异或的按位贡献,我们转二进制统计某一位 0/1 出现次数,我们发现异或对答案的贡献是两个数不同,所以我们前缀和优化一下(或者总和扣掉那个数也行),我们枚举 \(a_k\),通过按位的贡献 \(O(1)\) 计算答案
点击查看代码
#include <bits/stdc++.h>
#define int long long
#define endl '\n'
using namespace std;
void solve(){
int n; cin>>n;
vector<int> a(n + 1);
vector<vector<int>> p0(n + 1,vector<int>(32)),p1(n + 1,vector<int>(32));
for(int i = 1;i<=n;i++) cin>>a[i];
for(int i = 1;i<=n;i++){
for(int j = 0;j<32;j++){
if((1ll<<j)&a[i]){
p1[i][j]++;
} else {
p0[i][j]++;
}
}
}
for(int i = 1;i<=n;i++){
for(int j = 0;j<32;j++){
p0[i][j] += p0[i-1][j];
p1[i][j] += p1[i-1][j];
}
}
int ans = 0;
for(int i = 1;i<=n;i++){
int now = 0;
for(int j = 0;j<32;j++){
if((1ll<<j)&a[i]){
now += p0[i-1][j] * (1ll<<j);
now += (p0[n][j] - p0[i][j]) * (1ll<<j);
} else {
now += p1[i-1][j] * (1ll<<j);
now += (p1[n][j] - p1[i][j]) * (1ll<<j);
}
}
ans = max(now,ans);
}
cout<<ans<<endl;
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int T; cin>>T; while(T--)
solve();
return 0;
}
F题
首先我们考虑按照二维数组从左到右从上到下编号,序号是 \((i-1) \times m + j\),将 \(1 \sim k\) 按照序号顺序依次排下去,首先如果 \(m\) 不是 \(k\) 的倍数,这样每一行都会有错开,能保证上下不重复,如果 \(m\) 是 \(k\) 的倍数,则我们每一行手动往右边错开一位即可
点击查看代码
#include <bits/stdc++.h>
// #define int long long
#define endl '\n'
using namespace std;
const int P = 3e5;
void solve(){
int n,m,k; cin>>n>>m>>k;
if(m % k == 0){
for(int i = 1;i<=n;i++){
for(int j = 1;j<=m;j++){
cout<<(j+i-1)%k+1<<" ";
}
cout<<endl;
}
return;
}
for(int i = 1;i<=n;i++){
for(int j = 1;j<=m;j++){
cout<<((i-1)*m+j-1)%k+1<<" ";
}
cout<<endl;
}
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(0),cout.tie(0);
int T; cin>>T; while(T--)
solve();
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号