【vjudge训练记录】大一寒假专项训练——DFS

训练情况

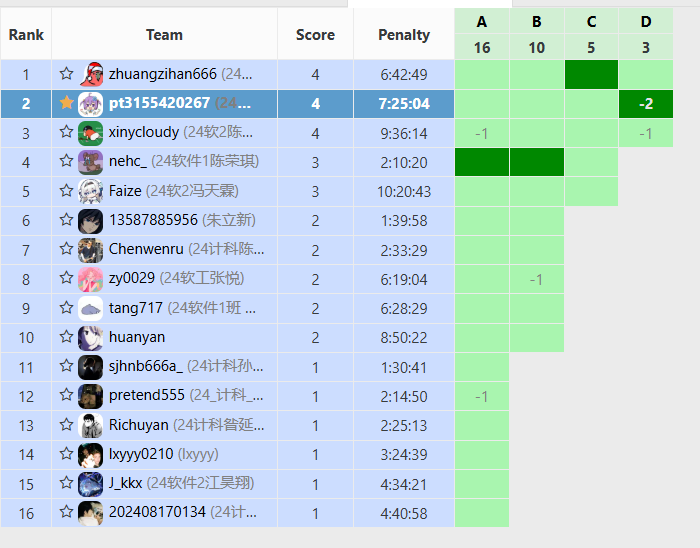
A题

全排列模板题，DFS函数传参目前在第几位，将当前位置设成 \(1 \sim n\) 中未被使用的数字，标记这个数字已使用 ，再递归下一位，同时记得回溯，在递归之后要把标记取消掉。直到递归出口当前位置 > n 时输出方案返回，代码时间复杂度 \(O(n!)\)

点击查看代码

#include <bits/stdc++.h>
// #define int long long
#define endl '\n'

using namespace std;

const int N = 11;

int n;
int a[N];
bool v[N];

void dfs(int x){
    if(x > n){
        for(int i = 1;i<=n;i++) cout<<setw(5)<<a[i];
        cout<<endl;
        return;
    }
    for(int i = 1;i<=n;i++){
        if(v[i]) continue;
        v[i] = 1;
        a[x] = i;
        dfs(x + 1);
        a[x] = 0;
        v[i] = 0;
    }
}

void solve(){
    cin>>n;
    dfs(1);
}

signed main(){
    // int T; cin>>T; while(T--)
    solve();
    return 0;
}

B题

二进制枚举 \(01\) 串，同上一题，只是不需要判断重复数字，值域在 \([0,1]\) 方法同上题，代码时间复杂度 \(O(2^n)\)

点击查看代码

#include <bits/stdc++.h>
// #define int long long
#define endl '\n'

using namespace std;

const int N = 11;

int n;
int a[N];

void dfs(int x){
    if(x > n){
        for(int i = 1;i<=n;i++){
            if(a[i]) cout<<"Y";
            else cout<<"N";
        }
        cout<<endl;
        return;
    }
    for(int i = 0;i<=1;i++){
        a[x] = i;
        dfs(x + 1);
        a[x] = 0;
    }
}

void solve(){
    cin>>n;
    dfs(1);
}

signed main(){
    // int T; cin>>T; while(T--)
    solve();
    return 0;
}

C题

DFS记忆化搜索，DFS函数传参 \((x,y)\) 表示当前位置坐标，表示滑雪起点为 \((x,y)\) 的最长长度，当前位置在雪场范围内可以往上下左右四个方向走，但是需要高度小于当前位置，直接递归下去直到无路可走时返回，注意每次返回的时候路径长度都要+1取大值，此时我们提交发现超时无法通过本题，这时有一个小优化，我们可以再开一个数组记录当前位置的最长路径长度，如果遇到直接返回值，不需要继续DFS搜索递归下去

点击查看代码

#include <bits/stdc++.h>
// #define int long long
#define endl '\n'

using namespace std;

const int N = 103;

int n,m;
int a[N][N];
int d[N][N];

int u[4][2] = {{-1,0},{0,-1},{1,0},{0,1}};

bool pd(int x,int y,int xx,int yy){
    return x>=1&&x<=n&&y>=1&&y<=m&&a[xx][yy]<a[x][y];
}

int dfs(int x,int y){
    if(d[x][y] != -1) return d[x][y];
    int now = 1;
    for(int i = 0;i<4;i++){
        int xx = x + u[i][0];
        int yy = y + u[i][1];
        if(!pd(xx,yy,x,y)) continue;
        now = max(now,dfs(xx,yy)+1);
    }
    d[x][y] = now;
    return now;
}

void solve(){
    cin>>n>>m;
    for(int i = 1;i<=n;i++){
        for(int j = 1;j<=m;j++){
            cin>>a[i][j];
            d[i][j] = -1;
        }
    }
    int ans = 0;
    for(int i = 1;i<=n;i++){
        for(int j = 1;j<=m;j++){
            ans = max(ans,dfs(i,j));
        }
    }
    cout<<ans<<endl;
}

signed main(){
    // int T; cin>>T; while(T--)
    solve();
    return 0;
}

D题

我们观察到燃放方案较少，我们可以考虑 \(01\) 二进制枚举，代表这个燃放方案放还是不放，如果为合法方案则更新答案最小值，判断合法时我们只需要把所有选择的燃放方案的 \(1\) 全部合在一起，去判断空地是否存在未燃放，或者摆杂物的地方燃放了，代码实现较复杂，详情见代码，代码时间复杂度 \(O(2^qqnm)\)

点击查看代码

#include <bits/stdc++.h>
// #define int long long
#define endl '\n'

using namespace std;

const int N = 11;

int n,m,q;
int d[N];
string s[N];
string t[N][N];
int ans = 100;
vector<int> opt;

void pd(){
    int cnt = 0;
    for(int i = 1;i<=q;i++) if(d[i]) cnt++;
    char v[N][N]; for(int i = 0;i<n;i++) for(int j = 0;j<m;j++) v[i][j]='0';
    for(int i = 1;i<=q;i++){
        if(!d[i]) continue;
        for(int j = 0;j<n;j++){
            for(int k = 0;k<m;k++){
                if(t[i][j][k] == '1') v[j][k] = '1';
            }
        }
    }
    for(int i = 0;i<n;i++){
        for(int j = 0;j<m;j++){
            if(s[i][j] == v[i][j]) return;
        }
    }
    if(cnt < ans){
        ans = cnt;
        opt.clear();
        for(int i = 1;i<=q;i++) if(d[i]) opt.emplace_back(i);
    }
}

void dfs(int x){
    if(x > q){
        pd();
        return;
    }
    for(int i = 0;i<=1;i++){
        d[x] = i;
        dfs(x + 1);
        d[x] = 0;
    }
}

void solve(){
    cin>>n>>m>>q;
    for(int i = 0;i<n;i++) cin>>s[i];
    for(int i = 1;i<=q;i++){
        for(int j = 0;j<n;j++) cin>>t[i][j];
    }
    dfs(1);
    if(ans==100) cout<<-1<<endl;
    else {
        cout<<ans<<endl;
        for(int i = 0;i<opt.size();i++) cout<<opt[i]<<" ";
    }
}

signed main(){
    // int T; cin>>T; while(T--)
    solve();
    return 0;
}