【牛客训练记录】牛客周赛 Round 69

训练情况

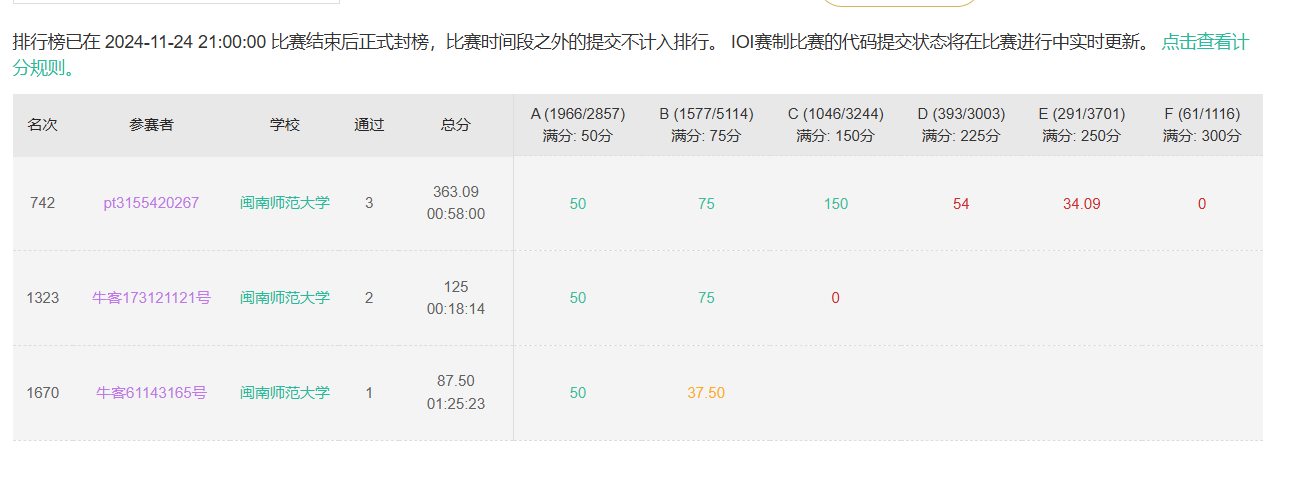
赛后反思

好吧，D 题没想到二进制枚举，以为 \(O(2^knm)\) 不可做。。。

A题

要求要等差数列，我们先求公差，为两元素的最大值-最小值，再在最大值的基础上加上公差即可。

#include <bits/stdc++.h>
// #define int long long
#define endl '\n'

using namespace std;

void solve(){
    int a,b; cin>>a>>b;
    cout<<max(a,b) + max(a,b) - min(a,b);
}

signed main(){
    // int T; cin>>T; while(T--)
    solve();
    return 0;
}

B题

我竟然没想到 scanf ，我超，这题直接 scanf 读入两个 long long 再相减即可，写了字符串做法，字符串做法就是找 , ，之后把字符串变成数字，答案是 \(b-a-1\)。

#include <bits/stdc++.h>
#define int long long
#define endl '\n'

using namespace std;

void solve(){
    string s; cin>>s;
    int n = s.size();
    int pos = 0;
    for(int i = 0;i<n;i++){
        if(s[i] == ','){
            pos = i;
            break;
        }
    }
    int a = 0;
    for(int i = pos+1;i<n;i++){
        if(s[i] == ',') break;
        a*=10;
        a+=s[i] - '0';
    }
    for(int i = n-1;i;i--){
        if(s[i] == ','){
            pos = i;
            break;
        }
    }
    int b = 0;
    for(int i = pos+1;i<n;i++){
        b*=10;
        b+=s[i] - '0';
    }
    cout<<b-a-1<<endl;
}

signed main(){
    // int T; cin>>T; while(T--)
    solve();
    return 0;
}

C题

我们考虑可以将终点关于水面进行对称，已知中点和一边，求另外一边的公式为 \(2 \times mid - l\)，所以我们直接 \(2 \times m - z\) 求出对称的另一点高度，所以向量就是 \((x,y,2m-z)\)，求三数的 gcd 再除化成最简即可，这题 int 会溢出，需要开 long long。

#include <bits/stdc++.h>
#define int long long
#define endl '\n'

using namespace std;

void solve(){
    int n,m; cin>>n>>m;
    for(int i = 1;i<=n;i++){
        int x,y,z; cin>>x>>y>>z;
        int ansx = x;
        int ansy = y;
        int ansz = 2*m-z;
        int g = __gcd(ansx,__gcd(ansy,ansz));
        cout<<ansx/g<<" "<<ansy/g<<" "<<ansz/g<<endl;
    }
}

signed main(){
    // int T; cin>>T; while(T--)
    solve();
    return 0;
}