【牛客训练记录】北京信息科技大学第十六届程序设计竞赛
训练情况
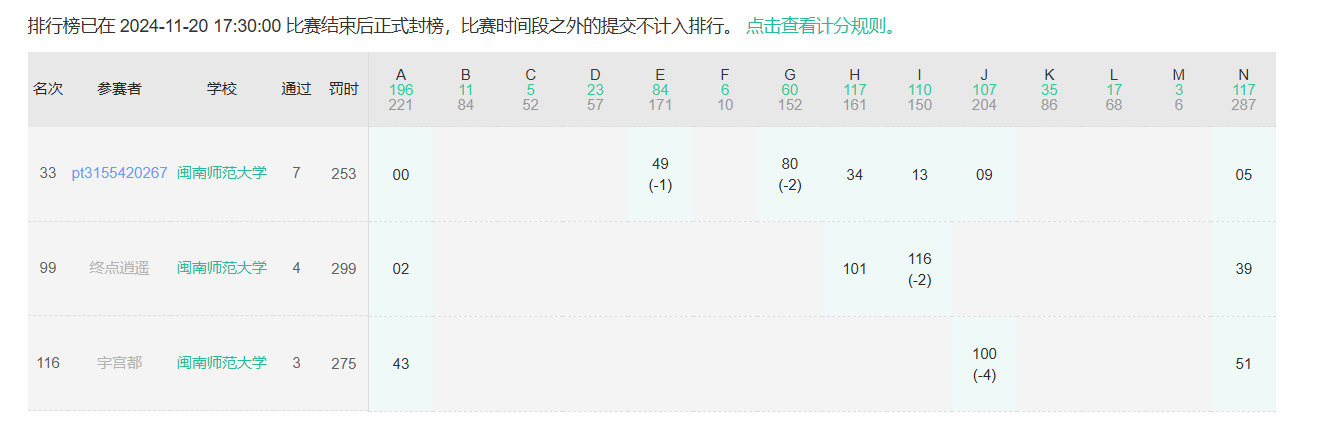
赛后反思
K题是简单DP,没看出来
A题
分类讨论找不同
#include <bits/stdc++.h>
#define int long long
using namespace std;
void solve(){
int a,b,c; cin>>a>>b>>c;
if(a==b) cout<<c<<endl;
else if(b == c) cout<<a<<endl;
else cout<<b<<endl;
}
signed main(){
// int T; cin>>T; while(T--)
solve();
return 0;
}
E题
我们每次可以选择区间 \([1,i]\) 进行翻转,要使得序列最后有序,首先我们必须将有序的部分放到后面,因为区间 \([1,i]\) 操作会使前面的部分翻转,导致原有的有序性被破坏,所以我们考虑先把序列翻转成 \([n,n-1,n-2,\cdots,3,2,1]\) 这种,所以我们直接循环 \(1 \sim n\) 找对应数的下标,将其先翻转到第一个,然后再翻转区间 \([1,n-i+1]\) 把这个数字放在后面的有序部分,这样子接下来的操作不会影响到后面的有序部分,最后再进行一次区间 \([1,n]\) 翻转即可。
#include <bits/stdc++.h>
#define int long long
using namespace std;
void solve(){
int n; cin>>n;
int tot = n;
vector<int> a(n + 1);
for(int i = 1;i<=n;i++) cin>>a[i];
vector<int> ans;
for(int i = 1;i<=n;i++){
for(int j = 1;j<=n-i+1;j++){
if(a[j] == i){
if(j == n-i+1) continue;
ans.push_back(j);
reverse(a.begin() + 1,a.begin() + 1 + j);
ans.push_back(n-i+1);
reverse(a.begin() + 1,a.begin() + 1 + n - i + 1);
}
}
}
ans.push_back(n);
cout<<ans.size()<<endl;
for(auto i:ans) cout<<i<<" ";
cout<<endl;
}
signed main(){
int T; cin>>T; while(T--)
solve();
return 0;
}
G题
这题我们容易想到贪心的思维,因为因为长度为 \(n\) 的数组进行 MEX 元素最大的值域只能到 \(n\),所以对于较大的元素我们是不需要 MEX 的,首先我们对数组进行排序,再求一个后缀和,枚举 MEX 的值,对于小于边界的部分进行 MEX,大于边界的部分直接求和,所以最后的答案就是 \(i^2+\sum_{j=i}^{n}a_j\) 取大值即可。
#include <bits/stdc++.h>
#define int long long
using namespace std;
void solve(){
int n; cin>>n;
vector<int> a(n + 1);
for(int i = 1;i<=n;i++) cin>>a[i];
sort(a.begin() + 1,a.end());
vector<int> suf(n + 3);
suf[n] = a[n];
for(int i = n-1;i;i--) suf[i] = suf[i+1] + a[i];
int ans = 0;
for(int i = 0;i<=n;i++){
ans = max(ans,i*i+suf[i+1]);
// cout<<i*i<<" "<<suf[i+1]<<endl;
}
cout<<ans<<endl;
}
signed main(){
int T; cin>>T; while(T--)
solve();
return 0;
}
H题
这题我们单独考虑进位对答案的贡献,对于一个数 \(x\),首先肯定需要 \(x\) 秒,接下来就是考虑进位的情况了,最低位对答案的多余贡献为 \(\lfloor \frac{x}{10} \rfloor\) ,比如 \(12345\) 这个数显然最低位会进位 \(1234\) 次,其次的低位会进位 \(123\) 次,依次类推,所以 \(12345\) 的答案就是 \(12345 + 1234 + 123 + 12 + 1\),我们使用 while 循环对答案进行累加即可。
#include <bits/stdc++.h>
#define int long long
using namespace std;
void solve(){
int x; cin>>x;
int ans = x;
while(x){
x/=10;
ans+=x;
}
cout<<ans<<endl;
}
signed main(){
int T; cin>>T; while(T--)
solve();
return 0;
}
I题
我们直接模拟,开一个变量记录当前位置,往某一边先往某一边再改方向即可。
#include <bits/stdc++.h>
#define int long long
using namespace std;
void solve(){
int n,k; cin>>n>>k;
char s[n+1];
getchar();
for(int i = 1;i<=n;i++) cin>>s[i];
int pos = k;
int ans = 0;
while(pos>=1&&pos<=n){
if(s[pos] == '<'){
s[pos] = '>';
pos--;
} else if(s[pos] == '>'){
s[pos] = '<';
pos++;
}
ans++;
}
cout<<ans<<endl;
}
signed main(){
int T; cin>>T; while(T--)
solve();
return 0;
}
J题
这题每一个段的长度都是最后一个数字,这题我们考虑倒着想,最后一段的长度就是最后一个元素,那我们就可以从后面往前推导每一段了,所以我们从最后面开始往前看看是否能划分即可。
#include <bits/stdc++.h>
#define int long long
using namespace std;
void solve(){
int n; cin>>n;
vector<int> a(n + 1);
for(int i = 1;i<=n;i++) cin>>a[i];
int pos = n;
int ans = 0;
while(pos>0){
pos -= a[pos];
ans++;
}
if(pos==0) cout<<ans<<endl;
else cout<<-1<<endl;
}
signed main(){
int T; cin>>T; while(T--)
solve();
return 0;
}
K题
段首和段尾都可以代表段长度,这题需要用到DP(动态规划)的算法,dp[i] 代表 1 ~ i 的最大段数,首先我们对 dp 数组进行全部初始化成无穷大,对于每一个位置 i,只要 i - a[i] 和 i + a[i] - 1 没有超出边界,对于每一个位置 i 可以从 i 位置往左 a[i] 个位置 往右 a[i] 个位置转移而来,所以动态规划状态转移方程为 dp[i]=min(dp[i],dp[i-a[i]]+1) / dp[i+a[i]-1]=min(dp[i+a[i]-1],dp[i-1]+1) ,最后我们判断 dp[n] 即(1~n)是否被更新过,如果是无穷大就是无解输出 -1,否则就是有解,直接输出 dp[n] 的值即可。
#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define pb push_back
#define se second
#define fi first
//#define int long long
const int inf = 1e9 + 10;
void solve(){
int n;cin >> n;
vector<int> a(n + 1);
for(int i = 1 ; i <= n ; i++) cin >> a[i];
vector<int> dp(n + 1 , inf);
dp[0] = 0;
for(int i = 1 ; i <= n ; i++){
if(i + a[i] - 1 <= n ){
dp[i + a[i] - 1] = min(dp[i + a[i] - 1] , dp[i - 1] + 1);
}
if(i - a[i] + 1 > 0){
dp[i] = min(dp[i] , dp[i - a[i]] + 1);
}
}
cout << (dp[n] == inf ? -1 : dp[n]) << '\n';
}
signed main(){
ios::sync_with_stdio(false);
cin.tie(0);cout.tie(0);
int t = 1;
cin >> t;
while(t--){
solve();
}
return 0;
}
N题
分成两段,取每段下标最大的,所以我们 \(a_n\) 肯定会被选到,要保证答案最大,所以另一段我们就从下标 \(1 \sim n-1\) 中选最大的即可。
#include <bits/stdc++.h>
#define int long long
using namespace std;
void solve(){
int n; cin>>n;
vector<int> a(n + 1);
for(int i = 1;i<=n;i++) cin>>a[i];
int mi = a[1];
for(int i = 2;i<n;i++) mi = min(mi,a[i]);
cout<<mi+a[n]<<endl;
}
signed main(){
int T; cin>>T; while(T--)
solve();
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号