FFT(快速傅里叶变换)学习笔记
FFT(快速傅里叶变换)学习笔记
时间:2019.5.8
\(FFT\)(快速傅里叶变换)是一种用于处理多项式的快速算法
多项式乘法:给定一个 \(n\) 次多项式 \(F(x)\),和一个 \(m\) 次多项式 \(G(x)\)。
请求出 \(F(x)\) 和 \(G(x)\) 的卷积。
卷积是啥?能吃吗 qwq?
看完这篇文章,你就会明白如何用 \(FFT\) 解决这道题了。不过,在正式讲解前,我先问大家两个问题:
一个数字,它的 \(n\) 次方是 \(1\),请问它是什么?
我们知道,一个 \(2\) 次的方程可能会有 \(2\) 个解,\(3\) 次的方程可能会有 \(3\) 个解……那么这个问题会有 \(n\) 个解吗?
多项式
\(FFT\) 所指的 “多项式” 一般都是只有一元的多项式(即只有 \(x\) 一个字母),形如:
这是一个 \(n - 1\) 次 \(n\) 项式。下文的多项式也是指这样的式子。
乘法
多项式的乘法,在数学上称为 “卷积” 。
举个例子吧。
所以说,其实卷积就是多项式普通地相乘起来。
如果要让你计算两个多项式相乘的结果(还是一个多项式),你会怎么做?
我会暴力!ovo
// 让 a * b = c
// a[i] 表示 x^i 项的系数,b、c 同理
k = n + m // 结果多项式的次数,刚好等于两个多项式次数的总和
for (int i = 0; i <= k; i++) {
c[i] = 0;
for (int j = 0; j <= n; j++) {
c[i] += a[j] * b[i - j]; // 嗯?
}
}
不要吐槽 2 格缩进QAQ感到奇怪?为什么让 c[i] += a[j] * b[i - j] 呢?我们不妨手推一下样例试试(高能预警):
我们将 \(F\)、\(G\) 和 \(H\) 的系数拿出来看看?
好吧……可能不是很明显,但是 \(H\) 的第 \(i\) 项系数的确等于 \(\displaystyle \sum _ {j + k = i} f _ j g _ k\)。想想多项式乘在一起的过程吧。现在能够明白代码的意思了吗?
但,但暴力的复杂度明显是 \(\mathrm {O} (N ^ 2)\) 的啊……有没有更快的算法呢?
圆与复数
一个数字,它的 \(n\) 次方是 \(1\),请问它是什么?
你会说:它是 1。嗯,当 \(n\) 是偶数时,还可能是 -1,还有吗…好像没了。
听说过 \(i\) 吗?它也许能给我们一些启示。
i 的故事
定义 \(i ^ 2 = -1\)。
咦,不可能啊?实数的平方不是非负吗?没关系,这个 \(i\) 不是实数,实数的法则管不了它。
大家也许听说,\(i\) 的名字叫 虚数。
复数
实数和虚数的组合叫做复数。
比如 \(2 + 3i\) ,一次乘法,还有一次加法。
\(1 + 2 i ^ 2 + 3 i ^ 3 + 4 i ^ 4\)?不存在的。别忘了 \(i ^ 2 = -1\)!
真是奇怪的数……一个复数一般用形如 \(a + bi\) 的形式表示。正如实数对应着数轴上的点一样,每一个复数与平面上的一个点 \((a, b)\) 对应。这个平面被称为“复平面”。图中 \(2 + 3i\) 就对应着点 \((2, 3)\)。
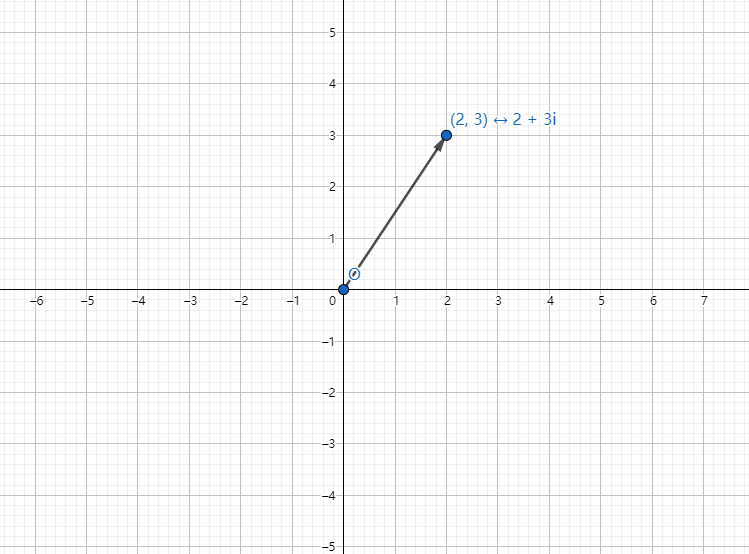
复数的 模长 指它的长度(到原点的距离),辐角 指它与原点的连线,与 \(x\) 轴(逆时针)的夹角。
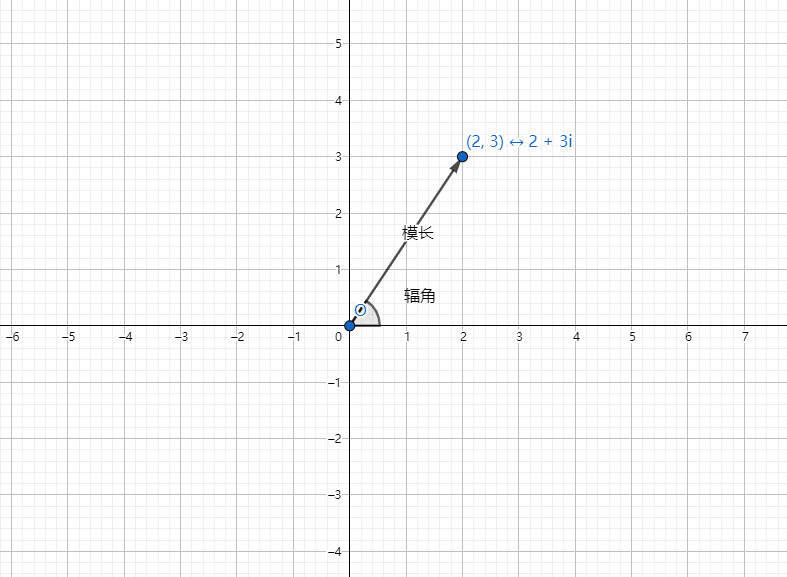
代码实现?用结构体存储复数,分别存下实部和虚部就行了。注意要用 double,以后会用到浮点数。
struct Complex {
double r, i; // 实部和虚部。r 和 i 分别是英文中“实部”和“虚部”的首字母。
// 以下是构造函数,看不懂不要紧。
Complex() : r(0), i(0) {}
Complex(double r, double i) : r(r), i(i) {}
Complex(const Complex& c) : r(c.r), i(c.i) {}
};
运算 - 加减法
既然是数,那肯定也有运算吧!复数既有加减法,又有乘除法。
(\(FFT\) 中用不到复数的除法,我们这里不讲。)
让我们试一试,将两个复数相加减会怎样?如果有两个复数分别是\(a _ 0 + b _ 0 i\) 和 \(a _ 1 + b _ 1 i\),加减得到:
\((a _ 0 + b _ 0 i) + (a _ 1 + b _ 1 i) = a _ 0 + b _ 0 i + a _ 1 + b _ 1 i = (a _ 0 + a _ 1) + (b _ 0 + b _ 1) i\)。嗯,实部虚部分别相加。
\((a _ 0 + b _ 0 i) - (a _ 1 + b _ 1 i) = a _ 0 + b _ 0 i - a _ 1 - b _ 1 i = (a _ 0 - a _ 1) + (b _ 0 - b _ 1) i\)。嗯,实部虚部分别相减。
(不要怕,简单的拆括号和合并同类项而已)
诶?我们说复数对应平面上的点,那么复数加减有什么几何意义吗?
如图,有两个复数 \(2 + 3i\) 和 \(3 + 1i\)。
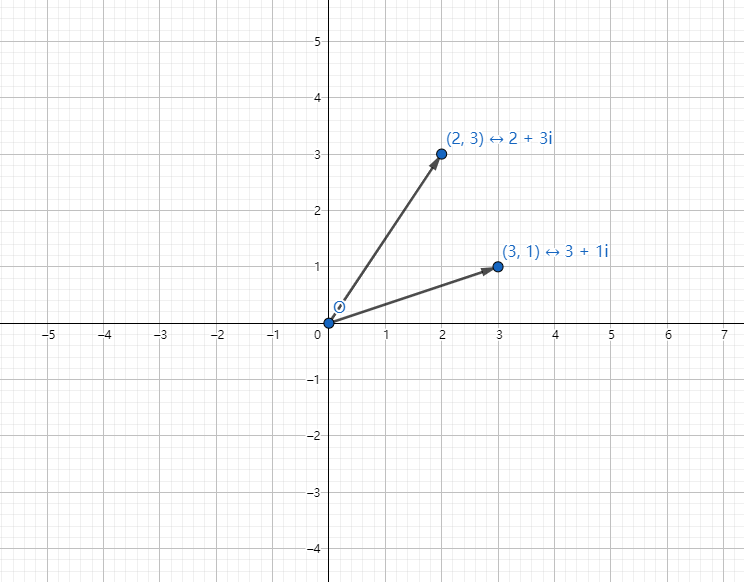
观察它们相加的结果,\((2 + 3i) + (3 + 1i) = 5 + 4i\)
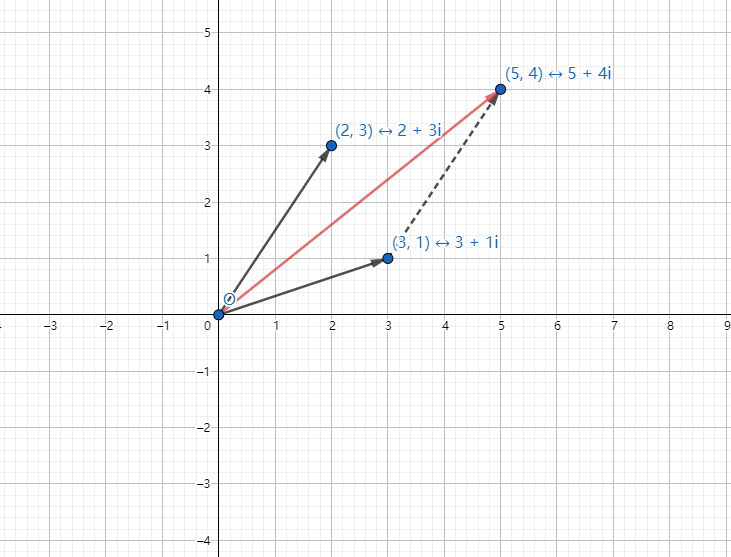
没错。它们相加的结果可以看成在 \(3 + 1i\) 的端点处向上数 \(3\) 格,向右数 \(2\) 格得到的点。或者说是两个复数所组成平行四边形的一条对角线。(理解一下这句话)
减法呢?\(a - b = a + (-b)\) 嘛。\((-b)\) 就是复数 \(b\) 关于原点的对称点。画个图试试看!
学过向量的同学可以发现:复数加减法的规则和向量加减法是一样的。
因此我们也可以把复数看成是向量,而非点。
代码:
// 重载运算
inline Complex operator+(const Complex& a, const Complex& b) {
return Complex(a.r + b.r, a.i + b.i);
}
inline Complex operator-(const Complex& a, const Complex& b) {
return Complex(a.r - b.r, a.i - b.i);
}
运算 - 乘法
乘法呢?好像麻烦一点
\( (a _ 0 + b _ 0 i) \times (a _ 1 + b _ 1 i) \\ = a _ 0 \times (a _ 1 + b _ 1 i) + b _ 0 i \times (a _ 1 + b _ 1 i) \\ = a _ 0 \times a _ 1 + a _ 0 \times b _ 1 i + b _ 0 i \times a _ 1 + b _ 0 i \times b _ 1 i \\ = a _ 0 a _ 1 + a _ 0 b _ 1 i + b _ 0 a _ 1 i - b _ 0 b _ 1 \)
别忘了 \(i ^ 2 = -1\),接下来合并一下同类项。
\(= (a _ 0 a _ 1 - b _ 0 b _ 1) + (a _ 0 b _ 1 + b _ 0 a _ 1) i\)
于是我们就得到了乘法的公式:
inline Complex operator*(const Complex& a, const Complex& b) {
return Complex(a.r * b.r - a.i * b.i, a.r * b.i + a.i * b.r);
}
复数乘法也有几何意义。模长相乘,辐角相加。怎么推出来的呢?留给大家去思考。
给大家一点提示吧:
可以推出 \((a _ 0 + b _ 0 i) \times (a _ 1 + b _ 1 i) = a _ 0 \times (a _ 1 + b _ 1 i) + b _ 0 \times (-b _ 1 + a _ 1 i)\)。点 \((a _ 1, b _ 1)\) 与原点的连线和点 \((-b _ 1, a _ 1)\) 与原点的连线是什么关系呢?


 浙公网安备 33010602011771号
浙公网安备 33010602011771号