芝士：AC自动机

目录

• 背景
• 前置芝士
  • Trie
  • KMP
• 做什么
• 思路
  • 预处理
  • 主要想法
  • fail指针
    • 做什么
    • 怎样求
      • 代码
  • 查询有多少个模式串在文本串中出现过
    • 思路
    • 代码
  • 查询每一个模式串在文本串中出现的次数
    • 思路
    • 代码

背景

为了解决字符串问题而出来的数据结构

前置芝士

Trie

就是通过树这种树形结构，充分利用LCP的树形结构

举个栗子：

我们有字符串:

abd

abe

ab

ba

他们的Trie长成这样

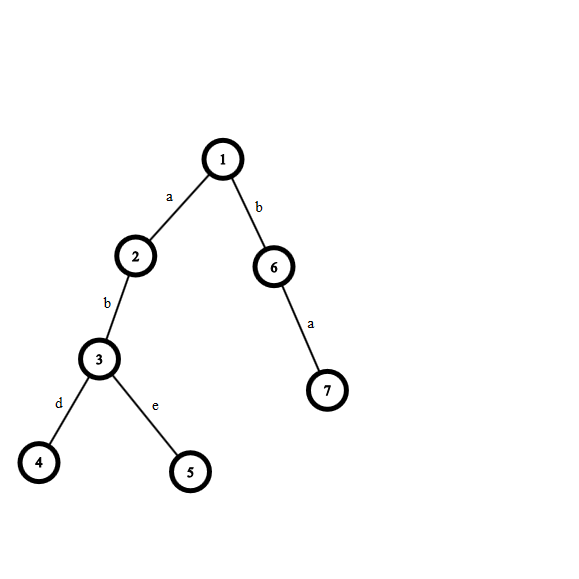
KMP

简单一句话而言：继承革命烈火！

为何如此而言？

对于文本串，我们假设当前的元素为\(i\)

对于模式串，我们假设当前的元素为\(j\)

我们要考虑的其实就是\(c_i\)与\(s_j\)不相同

如果不相同，我们就要返回去从\(i-j+2\)开始匹配

但是，我们都已经虽然\(c_i\neq s_j\)，但是我们可以之前是匹配的啊

所以，我们可以不用退这么多

我们只需要知道当前的最长后缀与最长的哪一个前缀是一样的，再将\(j\)指过来就行了

乍一看时间复杂度好像没变

但是巨佬们说这样的方法均摊是\(O(n)\)

还是不懂？

机房巨佬PPL的博客

做什么

给定n个模式串，求有多少个模式串在文本串中出现过

思路

预处理

将模式串建成Trie

主要想法

借用KMP的思想，我们每一次的匹配尽量使用已经有的最长前缀

fail指针

做什么

如果\(fail_i==j\)

那么\(root\)到\(j\)的字符串是\(root\)到\(i\)的字符串的一个后缀

所以你明白了吧，通过这个fail，我们可以每次不从根节点开始比较，这大大减少了时间复杂度

注意这个fail数组是失配数组，也就是当前这个不能匹配，下一次应该从哪一个点开始匹配

怎样求

也许你感觉这个fail数组一听起来就非常的难求，但是，出乎意料，他很好求

首先一点，\(dep_{fail_i}< dep_i\)，这通过fail的定义就能容易的知道

第一层的fail一定是根节点，这就是初始化

我们考虑一个点u和u的父亲fa

如果\(fail_{fa}\)和\(u\)的儿子都为v的，那么\(fail_u=v\)

如果不行呢？

继续跳不就完了？

代码

void init_fail()
{
	queue<int> q;
	for(int i=0;i<26;i++)
	{
		if(tre[0].vis[i])
		{
			tre[tre[0].vis[i]].fail=0;
			q.push(tre[0].vis[i]);
		}
	}
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		for(int i=0;i<26;i++)
		{
			if(tre[u].vis[i])
			{
				tre[tre[u].vis[i]].fail=tre[tre[u].fail].vis[i];
				q.push(tre[u].vis[i]);
			}
			else
				tre[u].vis[i]=tre[tre[u].fail].vis[i];
		}
	}
}

查询有多少个模式串在文本串中出现过

思路

很明显，有了fail数组之后，我们用fail数组在树上反复跳跃就行了

代码

int matching(char s[])//有多少个模式串出现
{
	int lens=strlen(s);
	int ans=0;
	int now=0;
	for(int i=0;i<lens;i++)
	{
		now=tre[now].vis[s[i]-'a'];
		for(int t=now;t&&tre[t].f==0;t=tre[t].fail)
		{
			ans+=tre[t].end;
			tre[t].f=1;
		}
	}
	return ans;
}

查询每一个模式串在文本串中出现的次数

思路

根据机房巨佬JZM所言，将fail数组建成一颗树，之后书上查分即可

代码

void count(char s[],int tot[])//每一个模式串出现了多少次
{
	queue<int> q;
	int ans[MAXN]={};
	int lens=strlen(s);
	int now=0;
	for(int i=0;i<lens;i++)
	{
		now=tre[now].vis[s[i]-'a'];
		ans[now]++;
	}
	for(int i=1;i<=cnt;i++)
		if(!in[i])
			q.push(i);
	while(!q.empty())
	{
		int u=q.front();
		q.pop();
		if(tre[u].end)
		{
			for(auto it:tre[u]._ind)	
				tot[it]=ans[u];
		}
		int v=tre[u].fail;
		ans[v]+=ans[u];
		in[v]--;
		if(in[v]==0)
			q.push(v);
	}
}