习题：逛公园（记忆化搜索）

 

题目

策策同学特别喜欢逛公园。公园可以看成一张N个点M条边构成的有向图，且没有 自环和重边。其中1号点是公园的入口，N号点是公园的出口，每条边有一个非负权值， 代表策策经过这条边所要花的时间。
策策每天都会去逛公园，他总是从1号点进去，从N号点出来。
策策喜欢新鲜的事物，它不希望有两天逛公园的路线完全一样，同时策策还是一个 特别热爱学习的好孩子，它不希望每天在逛公园这件事上花费太多的时间。如果1号点 到N号点的最短路长为d，那么策策只会喜欢长度不超过d+K的路线。
策策同学想知道总共有多少条满足条件的路线，你能帮帮它吗？
为避免输出过大，答案对P取模。
如果有无穷多条合法的路线，请输出−1。

输入格式

第一行包含一个整数 T, 代表数据组数。
接下来T组数据，对于每组数据： 第一行包含四个整数 N,M,K,P每两个整数之间用一个空格隔开。
接下来MMM行，每行三个整数ai,bi,ci代表编号为ai,bi的点之间有一条权值为ci的有向边，每两个整数之间用一个空格隔开。

输出格式

输出文件包含 T 行，每行一个整数代表答案。

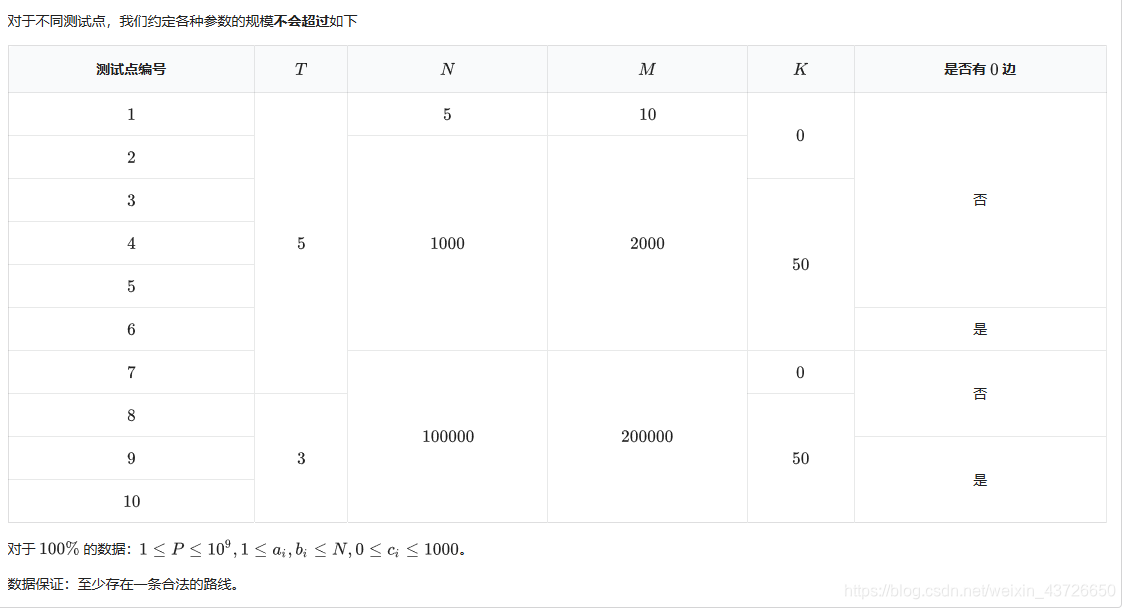
数据范围

思路

刚看到这题还是挺懵逼的，最短路&求路数？
wtf？

在仔细看看，发现k挺小的，
之后，f[i][j]表示到i号节点长度不大于dis[i]+j的个数，
之后，先用dij跑反向图
再用记忆化搜索跑正向图。。。
作者因dij而自闭
至于-1的情况，其实就是判断图中有没有0环
某位大犇的拓扑排序解法

代码

#include<iostream>
#include<vector>
#include<cstring>
#include<climits>
#include<queue>
#include<cstdio>
using namespace std;
#define int long long
struct edge
{
    int v;
    int w;
    int nxt;
}e0[200005],e1[200005];
struct node
{
    int v;
    int w;
    friend bool operator < (const node &a,const node &b)
    {
        return a.w<b.w;
    }
};
int t;
int n,m,k,p,ppl;
int head0[100005];
int head1[100005];
int dis[100005];
int dp[100005][55];
bool f[100005][55];
void read(int &x)
{
    x=0;
    int f=1;
    char c=getchar();
    while('0'>c||c>'9')
    {
        if(c=='-')
            f=-1;
        c=getchar();
    }
    while('0'<=c&&c<='9')
    {
        x=(x<<3)+(x<<1)+c-'0';
        c=getchar();
    }
    x*=f;
}
void write(int x)
{
    if(x<0)
    {
        putchar('-');
        write(-x);
        return;
    }
    if(x<10)
    {
        putchar(x+'0');
    }
    else
    {
        write(x/10);
        putchar(x%10+'0');
    }
}
void Add_Edge(int x,int y,int z)
{
	e0[++ppl].nxt = head0[x];
	e0[ppl].v = y;
	e0[ppl].w = z;
	head0[x] = ppl;
	e1[ppl].nxt = head1[y];
	e1[ppl].v = x;
	e1[ppl].w = z;
	head1[y] = ppl;
}
void init()
{
    ppl=0;
    memset(dis,127,sizeof(dis));
    for(int i=0;i<=n;i++)
    {    	for(int j=0;j<=k;j++)
    	{
    		f[i][j]=0;
    		dp[i][j]=0;
    	}
    }
    for(int i=1;i<=n;i++)
    {
    	head1[i]=0;
    	head0[i]=0;
    }
}
void dij()
{
    dis[n]=0;
	queue<int> q;
    q.push(n);
    while(!q.empty())
    {
        int u=q.front();
        q.pop();
        for(int i=head1[u]; i ;i=e1[i].nxt)
        {
            int v=e1[i].v;
            if(dis[v]>dis[u]+e1[i].w)
            {
                dis[v]=dis[u]+e1[i].w;
                q.push(v);
            }
        }
    }
}
int solve(int now,int ne)
{
    if(f[now][ne])
        return -1;
    if(dp[now][ne])
        return dp[now][ne];
    f[now][ne]=1;
    if(now==n)
        dp[now][ne]=1;
    else
        dp[now][ne]=0;
    for(int i=head0[now]; i ;i=e0[i].nxt)
    {
        int v=e0[i].v;
        int t=dis[v]+e0[i].w-dis[now];
        if(t<=ne)
        {
            int w=solve(v,ne-t);
            if(w==-1)
            {
                dp[now][ne]=-1;
                return -1;
            }
            dp[now][ne]+=w;
            if(dp[now][ne]>=p)
                dp[now][ne]-=p;
        }
    }
    f[now][ne]=0;
    return dp[now][ne];
}
void c_in()
{
    read(n);
    read(m);
    read(k);
    read(p);
    init();
    for(int i=1;i<=m;i++)
    {
        int s,e,w;
        read(s);
        read(e);
        read(w);
        Add_Edge(s,e,w);
    }
    dij();
    write(solve(1,k));
    putchar('\n');
}
signed main()
{
    read(t);
    for(int i=1;i<=t;i++)
        c_in();
    return 0;
}