算法模型总结:螺旋升天矩阵
文章目录
螺旋升天矩阵总结
本文将持续更新
零、前言
螺旋矩阵遍历,其实本身是一个描述类问题,本来不想总结,但由于lc把它标为简单题,导致人在极度愤怒的情况下做不明白。故想总结一下。
在处理描述性问题的时候,一定要找规律尤其是不变的方法。
一、正方形螺旋矩阵
59. 螺旋矩阵 II
1.思路
- 层层扒皮,层层遍历
- 遍历方式:每一行(列)遍历n-1个元素(n为一行中的元素个数)
- 处理结束时的情况:可能是一个元素,可能是一列或者一行元素。此时我们无法向以上那样扒皮遍历了。正方形最终结束的方式只能是下图中的方式,或者中间有一个元素的方式。而下图中的方式是符合我们的扒皮规则的,因此只需要将最后只有一个的方式单独拎出来就好。
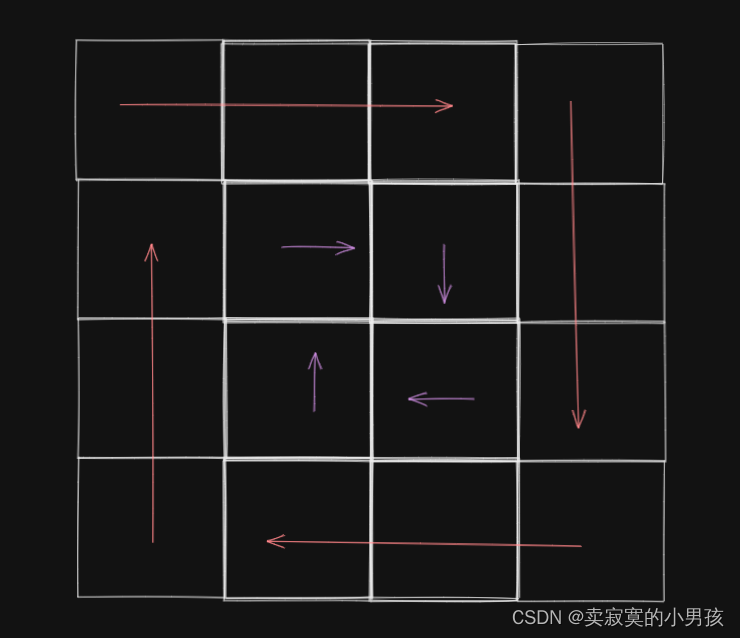
2.实现
class Solution {
public:
vector<vector<int>> generateMatrix(int n) {
vector<vector<int>> arr;
arr.resize(n);
for(int i=0;i<n;i++)
{
arr[i].resize(n);
}
int m=arr[0].size();
int i=0;
int j=0;
int count=1;
while(i<=((m+1)/2-1))//(i,i)为一圈的起始位置
{
int d=n-i*2;//d表示这一圈有几个元素
if(d==1)
{
arr[i][i]=count;
}
int a=i;
int b=i;
while(b<i+d-1)
{
arr[a][b]=count;
count++;
b++;
}
while(a<i+d-1)
{
arr[a][b]=count;
count++;
a++;
}
while(b>i)
{
arr[a][b]=count;
count++;
b--;
}
while(a>i)
{
arr[a][b]=count;
count++;
a--;
}
i++;
}
return arr;
}
};
二、矩形矩阵
54. 螺旋矩阵
这个玩意真的折磨,题主在做的时候没有考虑周全矩阵的结束形状,导致花费了好多时间:
1.思路
1.只需要遍历的时候将正方形的边使用矩形的两边来表示。
2.当结束的时候,行或者列有一个为1,此时符合,需要特殊情况处理,类似正方形中只有一个元素。我的处理方式是直接使用两个for循环来加载所有元素。
2.实现
class Solution {
public:
vector<int> spiralOrder(vector<vector<int>>& matrix) {
vector<int> arr;
arr.resize(matrix.size()*matrix[0].size());
int a=0;//行下标
int b=0;//列下标
int i=0;//每一层起始位置
int d=0;//每一圈有几个元素
int count=0;//数组下标
int Row=matrix.size();
int Col=matrix[0].size();
int size=Row<Col?Row:Col;
int row=0;//每小圈的行
int col=0;//每小圈的列
while(i<=(size+1)/2-1)//计算循环几圈
{
row=Row-2*i;
col=Col-2*i;
a=i;
b=i;
if(row==1||col==1)
{
for(int m=a;m<row+a;m++)
{
for(int n=b;n<col+b;n++)
{
arr[count++]=matrix[m][n];
}
}
return arr;
}
while(b<i+col-1)
{
arr[count]=matrix[a][b];
count++;
b++;
}
while(a<i+row-1)
{
arr[count]=matrix[a][b];
count++;
a++;
}
while(b>i)
{
arr[count]=matrix[a][b];
count++;
b--;
}
while(a>i)
{
arr[count]=matrix[a][b];
count++;
a--;
}
i++;
}
return arr;
}
};
但是这段代码在剑指offer中是通过不了的,时间超时,但是在这里可以通过。
在剑指offer中看到了这样一种写死循环的写法,通过对边界的判定来结束死循环。
class Solution {
public:
vector<int> spiralOrder(vector<vector<int>>& matrix) {
if (matrix.size() == 0 || matrix[0].size() == 0)
return {};
vector<int> res;
int top = 0; //上边界
int bottom = matrix.size() - 1; //下边界
int left = 0; //左边界
int right = matrix[0].size() - 1; //右边界
while (true) {
// 从左到右
for (int i = left; i <= right; ++ i)
res.push_back(matrix[top][i]);
// 每次从左往右执行一次,则要往下移一层
if (++ top > bottom) break;
// 从上到下
for (int i = top; i <= bottom; ++ i)
res.push_back(matrix[i][right]);
// 每次从上到下执行一次,则要往左移一列
if (-- right < left) break;
// 从右到左
for (int i = right; i >= left; -- i)
res.push_back(matrix[bottom][i]);
// 每次从右到左执行一次,则要往上移一行
if (-- bottom < top) break;
// 从下到上
for (int i = bottom; i >= top; -- i)
res.push_back(matrix[i][left]);
// 每次从下到上执行一次,则要往右移一列
if (++ left > right) break;
}
return res;
}
};
三、总结
螺旋升天数组这类的描述型题目,非常考察统筹规划的能力,需要有一个明确清楚的思路再开始写代码,一般关键在于一层一层展开问题的时候找到那个统一的处理办法。
// 每次从下到上执行一次,则要往右移一列
if (++ left > right) break;
}
return res;
}
};
# 三、总结
螺旋升天数组这类的描述型题目,非常考察统筹规划的能力,需要有一个明确清楚的思路再开始写代码,一般关键在于一层一层展开问题的时候找到那个统一的处理办法。
<font color=red>本文将持续更新</font>



 浙公网安备 33010602011771号
浙公网安备 33010602011771号